数据在内存中的存储以及百度笔试题-编程知识

一.整型家族

什么是大小端存储（百度笔试题）

大端字节序存储

小端字节序存储

为什么要讨论大小端字节序存储

写一个程序判断是大端还是小端存储（百度笔试题）

思路：用1去判断，如果返回1则是小端，如果返回0则是大端。

例题1：输出结果：%d打印十进制有符号整型

第二题 %u打印无符号整数

第三题：

什么是截断：

第四题：

第五题

一.整型家族

char
unsigned char
sighned char 是否等于char取决于编译器
long
unsigned long [int]
sighned long [int]
short
unsigned short [int]
sighned char [int]
int
unsigned int
sighned int = int

二. 构造类型（自定义类型）

数组类型
结构体类型 struct
枚举类型 enum
联合类型 union

三.指针类型

四.空类型

五. 整数在内存中的存储

原码
反码
补码（内存中存的是补码）

最高位为符号位，其他位为有效位：有符号整型，

为什么数据存放在内存中要用补码的形式

什么是大小端存储（百度笔试题）

在内存中可以自定义顺序，但是只有从大到小，或者从小到大最为方便。

其中：

递增的如11 22 33 44 为大端存储
递减的如44 33 22 11 为小端存储

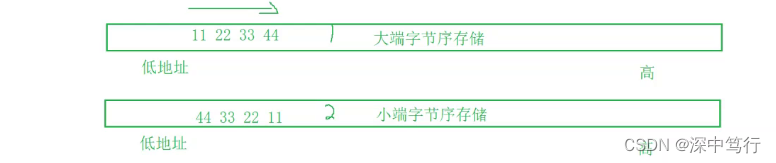
如地址：0x11223344 是十六进制，一位十六进制如1为0001占四个bit空间，11占8个bit空间，所以两个十六进制位占一个字符（8bit）。

大端字节序存储

0x11223344：将高字节如11放在低地址处，低位字节放在高地址处，为大端存储

小端字节序存储

0x11223344：将低字节如44放在低地址处，高位字节放在高地址处为小端存储

为什么要讨论大小端字节序存储

这是因为，如int型，占4个字节/8个字节，等等需要占多个字节才需要考虑顺序问题。

比如char型只用占一个字节，就不用考虑顺序问题。

写一个程序判断是大端还是小端存储（百度笔试题）

思路：用1去判断，如果返回1则是小端，如果返回0则是大端。

将1的二进制补码为0000 0000 ..... 0000 0001,那么它的十六进制为0x00 00 00 01，一个字节8位bit，所以在地址中存储为00 00 00 01，所以如果高地址是 1那么就是小端存储，返回0则是大端存储。

写法一：

int check_sys()
{int a = 1;char* p = (char*)&a;if (*p == 1)return 1;elsereturn 0;
}int main()
{if(check_sys()==1){printf("小端");}else{printf("大端");}return 0;
}

写法二：

int check_sys()
{int a = 1;if (*(char*)&a == 1)return 1;elsereturn 0;
}int main()
{if(check_sys()==1){printf("小端");}else{printf("大端");}return 0;
}

写法三：

int check_sys()
{int a = 1;return *(char*)&a;
}int main()
{if(check_sys()==1){printf("小端");}else{printf("大端");}return 0;
}

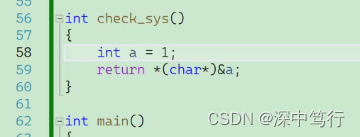
错误写法：这里a已经从内存取出来，a的类型已经成型了，不能在强制类型转换了。

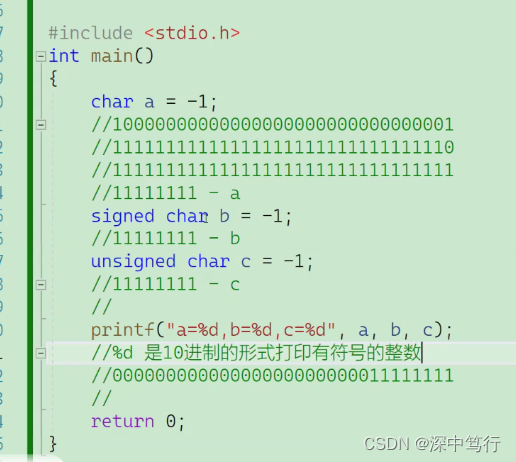
例题1：输出结果：%d打印十进制有符号整型

首先：-1的32位二进制位1000 0000 0000 0000 0000 0000 0000 0001

然后：转化为补码：1111 1111 1111 1111 1111 1111 1111 1111

由于是char型，一个字节只有8bit，所以-1为：1111 1111

由于是char型，打印为%d（是十进制有符号整型），所以要整型提升。

整型提升：由符号位决定

char = -1和signed char -1 ；符号位为1 ；所以将1111 1111 整型提升补1为1111 1111 1111 1111 1111 1111 1111 1111 转化为原码的十进制为-1.

unsigned char -1 整型提升，由于是无符号数，所有位数都是有效位，所以最高位用0补位，补位为0000 0000 0000 0000 0000 0000 1111 1111，由于他是无符号数，所以它是正数，所以补码就是原码，所以他是 255

第二题 %u打印无符号整数

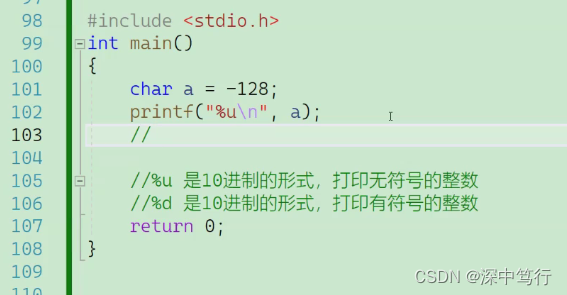
第一步：-128；计算机中原码：1000 0000 0000 0000 0000 0000 1000 0000

第二步：补码：1111 1111 1111 1111 1111 1111 1000 0000，所以计算机中只存1000 0000

第三步：由于是char型打印成无符号整型，所以要整型提升，由于char型是有符号所以用符号位1提升1111 1111 1111 1111 1111 1111 1000 0000；

第四步：由于是%u是无符号整型，所以所有位都是有效位，且无符号数原码反码补码相同，所以结果为

第三题：

虽然，char型只能存一个字节即8bit位，但是防不住初始化给你一个大于127的，所以就会发生截断。

128：原码 0000 0000 0000 0000 0000 0000 1000 0000，

补码 0111 1111 1111 1111 1111 1111 1000 0000

char只存放：1000 0000

整型提升：1111 1111 1111 1111 1111 1111 1000 0000

所以结果和上题一样。

什么是截断：

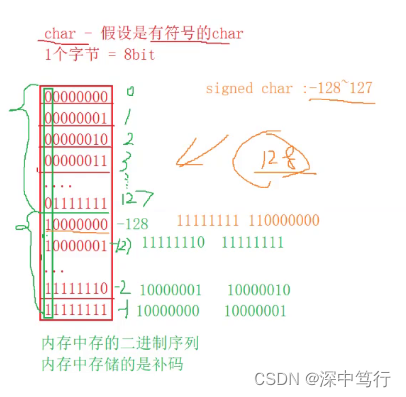
例如有符号char一个字节8为字符，其中第一位为符号位；无符号unsigned char 是从0-255，

有符号是从0-127，-127-（-1）。

所以超过127的部分，也等于127。超过255的地方也等于255。

特殊我们约定有符号 1000 0000，这里1是符号位，但是将补码按位取反加1，后超过8位，所以我们约定1000 0000 为-128.