【数据结构】12 堆栈应用：表达式求值-编程知识

【数据结构】12 堆栈应用：表达式求值

表达式类型

后缀表达式

有一个常量表达式的中缀表达式为：5 + 6 / 2 - 3 * 4，其后缀形式表示为： 5 6 2 / + 3 4 × -。后缀表达式的特点是运算符位于两个预算数之后。其前缀表达式为： - + 5 / 6 2 × 3 4。
后缀表达式相比于中缀表达式的求值要容易很多。
从左到右扫描该表达式：
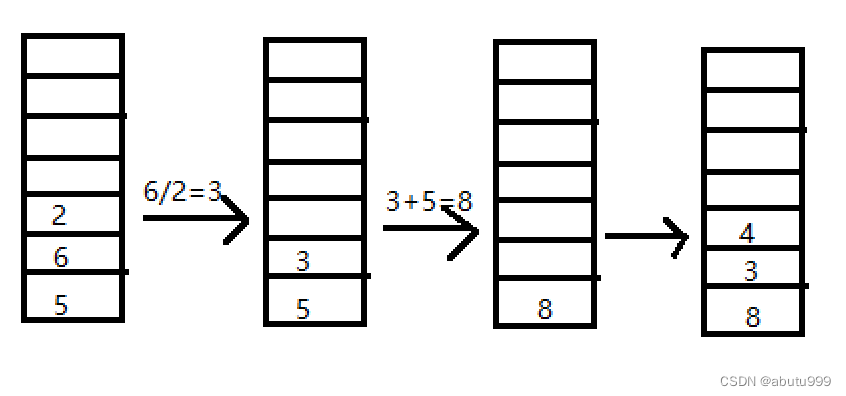
（1）遇见运算数5 6 2时不做计算，同时将5 6 2压入栈中。
（2）扫描到 / 时，把栈中最前的两个数取出，做运算得到结果3，压入栈中。
在这里插入图片描述
（3）扫描到运算符“+”，把序列里的最前面的两个数做运算，把结果8压入栈中。

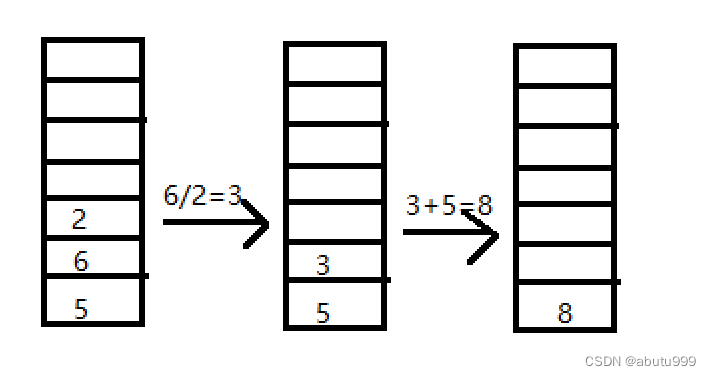
（4）遇见3 ，4 不做运算，压入栈中。

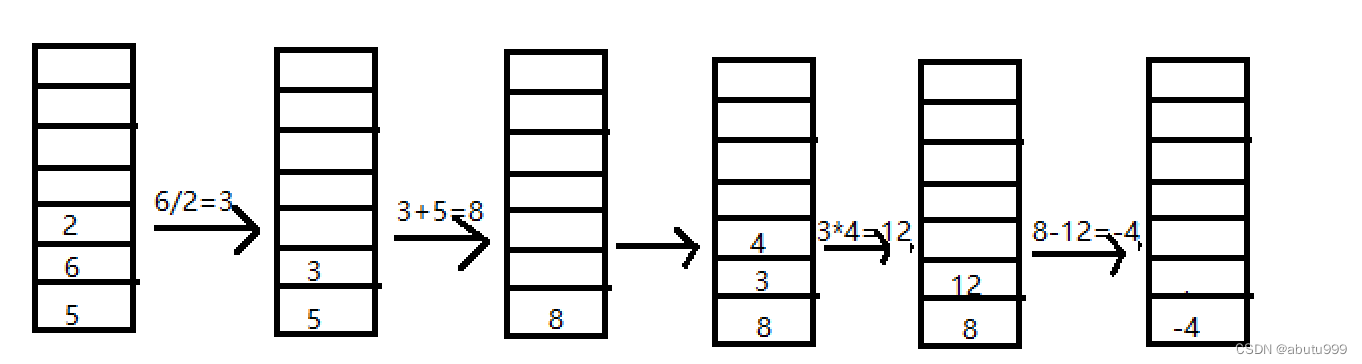
（5）扫描到运算符“*”，在栈中取出两个数做运算 3 * 4 = 12，将结果压入栈中。
（6）扫描到运算符“-”，在栈中取出两个数做运算8 -12 = -4。将结果压入栈中。
（7）最后不再有符号输入，则表示运算完成，将栈中最后一个值取出，即为运算结果。
在这里插入图片描述

代码实现

我们假设后缀表达式的对象用空格隔开，运算数为正实数。
思路：
先判断读入的字符类型：

数字：压入栈
运算符：从栈中取两个数字进行运算，运算结果压栈
结尾：从栈中取数字

# include <stdio.h>
#include < stdlib.h>
#include <ctype.h>typedef int ElementType;
typedef int Position;
typedef struct SNode* PtrToSNode;
typedef enum{num, opr, end} Type;struct SNode {ElementType* Data;Position Top;int MaxSize;};typedef PtrToSNode Stack;typedef struct DSNode* DStack;
struct DSNode
{ElementType* Data;Position Top1;Position Top2;int MaxSize;
};DStack CreateDStack(int MaxSize) {DStack S = (DStack)malloc(sizeof(DSNode) * 1);S->Data = (ElementType*)malloc(sizeof(ElementType) * MaxSize);S->Top2 = -1;S->Top1 = MaxSize;S->MaxSize = MaxSize;return S;
}bool PushX(DStack S, ElementType X, int Tag) {if (S->Top1 - S->Top2 == 1) {printf("the stack is full!\n");return false;}if (Tag == 1) {(S->Top1)--;S->Data[S->Top1] = X;}else{(S->Top2)++;S->Data[S->Top2] = X;}return true;
}ElementType PopX(DStack S, int Tag) {if (Tag == 1) {if (S->Top1 == S->MaxSize) {printf("the stack1 is empty!\n");return -1;}else {return S->Data[(S->Top1)++];}}else {if (S->Top2 == -1) {printf("the stack2 is empty!\n");return -1;}else {return S->Data[(S->Top2)--];}}}void print_ds(DStack S) {printf("print S1:\n");int t = S->Top1;while (t != S->MaxSize) {printf("Node: %d\n", S->Data[t]);(t)++;}printf("print S2:\n");t = S->Top2;while (t != -1) {printf("Node: %d\n", S->Data[t]);(t)--;}
}Stack CreateStack(int MaxSize) {Stack S = (Stack)malloc(sizeof(SNode) * 1);S->Data = (ElementType * )malloc(sizeof(ElementType) * MaxSize);S->Top = -1;S->MaxSize = MaxSize;return S;
}bool IsFull(Stack S) {if (S->Top == S->MaxSize - 1) {return true;}return false;
}bool Push(Stack S, ElementType X) {if (IsFull(S)) {printf("The Stack is full!\n");return false;}/*(S->Top)++;S->Data[S->Top] = X;*/S->Data[++(S->Top)] = X;return true;}bool IsEmpty(Stack S) {if (S->Top == -1) {return true;}return false;
}ElementType Pop(Stack S) {if (IsEmpty(S)) {printf("The Stack is empty!\n");return -1;}/*int temp = S->Data[S->Top];(S->Top)--;return temp;*/return (S->Data[(S->Top)--]);}void print_s(Stack S) {int t = S->Top;while (t != -1) {printf("Node: %d\n", S->Data[t]);(t)--;}
}Type Getop(char* Expr, int* start, char* str) {//跳过表达式前空格while (1) {str[0] = Expr[(*start)];(*start)++;if (str[0]  !=  ' ') {break;}}/*printf("str: %s\n", str);printf("start: %d\n", *start);*/int i = 0;while (str[i] != ' ' && str[i] != '\0') {i++;str[i] = Expr[*start];(*start)++;}/*printf("str: %s\n", str);printf("start: %d\n", *start);printf("i : %d\n", i);*/if (str[i] == '\0') {(*start)--;}str[i] = '\0';//printf("str: %s\n", str);if (i == 0) {return end;}else if (isdigit(str[0]) || isdigit(str[1])) {return num;}else {return opr;}}ElementType PostfixExp(char* Expr) {Stack S;S = CreateStack(100);int start = 0;Type T;char str[100];ElementType op1, op2;while ((T = Getop(Expr, &start, str)) != end) {if (T == num) {Push(S, atoi(str));}else {op1 = Pop(S);op2 = Pop(S);switch (str[0]){case '+': Push(S, op2 + op1); break;case '-': Push(S, op2 - op1); break;case '*': Push(S, op2 * op1); break;case '/': Push(S, op2 / op1); break;}}}if (!IsEmpty(S)) {op2 = Pop(S);}return op2;}int main() {char Expr[] = " 1 3 + 2 4 * -";ElementType f = PostfixExp(Expr);printf("f : %d\n", f);
}