Unity所有关于旋转的方法详解-编程知识

前言：欧拉角和四元数的简单描述

我们在Inspector面板上看到的rotation其实是欧拉角，

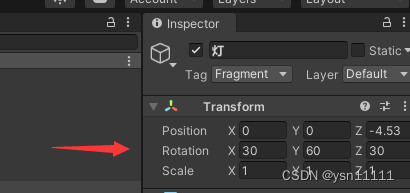
我们将Inspector面板设置成Debug模式，此时看到的local Rotation才是四元数。

Unity中的欧拉旋转是按照Z-X-Y顺规执行的旋转，一组欧拉旋转过程中，相对的轴向不会发生变化。 Transform.Rotate(new Vector3(30,60,30))，它代表执行了一组欧拉旋转，它相对的是旋转前的局部坐标朝向。正是这种顺规和轴向的定义，导致了万向节死锁的自然形成。

举个例子就是，在世界空间下，按照X-Y-Z去拖拽旋转轴，当拖拽到Z轴旋转时，X和Y轴的欧拉角都会改变，如果按照Z-X-Y去按顺序拖拽则轴与轴之间的数值不会影响。

代码表示:方式1和方式3的旋转结果相同

//方式一
transform.Rotate(30,60,30,Space.World);//方式二（X-Y-Z）
transform.Rotate(30,0,0,Space.World);
transform.Rotate(0,60,0,Space.World);
transform.Rotate(0,0,30,Space.World);//方式三（Z-X-Y）
transform.Rotate(0,0,30,Space.World);
transform.Rotate(30,0,0,Space.World);
transform.Rotate(0,60,0,Space.World);

欧拉角和四元数的相互转换：

// 欧拉角表示旋转
Vector3 eulerRotation = new Vector3(30f, 60f, 30f);
// 将欧拉角转换为四元数
Quaternion quaternionRotation = Quaternion.Euler(eulerRotation);
// 将四元数转换为欧拉角
Vector3 convertedEulerAngles = quaternionRotation.eulerAngles;

局部坐标系和世界坐标系的转换：

transform.up = transform.rotation * Vector3.up;
transform.right = transform.rotation * Vector3.right;
transform.forward = transform.rotation * Vector3.forward;

1.Transform旋转系列

(1)transform.Rotate（有万向锁）

public void Rotate (Vector3 eulers, Space relativeTo= Space.Self);

public void Rotate (float xAngle, float yAngle, float zAngle, Space relativeTo= Space.Self);

描述：这两种方式的旋转结果相同，应用一个围绕 Z 轴旋转 zAngle 度、围绕 X 轴旋转 xAngle度、围绕 Y 轴旋转 yAngle 度（按此顺序）的旋转。Space.Self代表局部坐标系，Space.World代表世界坐标系。

public void Rotate (Vector3 axis, float angle, Space relativeTo= Space.Self);

描述：用给定角度定义的度数围绕给定轴旋转该对象。

我们可以看个这样的例子：

transform.Rotate(Vector3.up, 30, Space.Self);
transform.Rotate(transform.up, 30, Space.World);

这两种旋转方式的结果是一致的。

(2)transform.RotateAround（有万向锁）

public void RotateAround (Vector3 axis, float angle);

public void RotateAround (Vector3 point, Vector3 axis, float angle);

描述：第一个参数为围绕的中心点，第二个参数为物体围绕转动的轴，方式1和方式2的区别在于，方式1围绕的中心点就是自己。

transform.RotateAround和transform.Rotate的区别就好比地球公转和自转的区别。

(3)transform.LookAt（无万向锁）

public void LookAt (Transform target, Vector3 worldUp= Vector3.up);

public void LookAt (Vector3 worldPosition, Vector3 worldUp= Vector3.up);

描述：旋转变换，使向前矢量指向 target 的当前位置。

主要是这句话的理解：

“随后它会旋转变换以将其向上方向矢量指向 worldUp 矢量暗示的方向。如果省略 worldUp 参数，则该函数会使用世界空间 y 轴。如果向前方向垂直于 worldUp，则旋转的向上矢量将仅匹配 worldUp 矢量。”

什么意思呢，就是LookAt的第一个参数决定了forward轴（蓝轴）的朝向，但是怎么旋转到目标位置还需要再确定一个轴，但是第二个参数并不等价于up轴（绿轴）指向worldUp,只是在保证forward轴（蓝轴）指向物体时，会尽量保证在旋转的过程中，up轴指向worldUp大致的方向，且不管怎么旋转up轴和worldUp夹角都不会超过90°。

2.Quaternion旋转系列（无万向锁）

创建旋转:

(1)Quaternion.LookRotation

public Quaternion LookRotation (Vector3 forward, Vector3 upwards= Vector3.up);

描述：物体的Z 轴指向forward，X 轴指向 forward 和 upwards 的差积，Y 轴指向 Z 和 X 之间的差积对齐。确定轴的顺序是Z-X-Y的顺序。

与LookAt的区别：

LookAt()与LookRotation()的参数都相似，但前者是将游戏对象的z轴指向参数所表示的那个点，而后者是将游戏对象的z轴指向参数所表示的向量的方向。

transform.LookAt(targetCube.transform);
transform.rotation = Quaternion.LookRotation(targetCube.transform.position-transform.position);

这两行代码的效果是等价的。

(2)Quaternion.FromToRotation

public static Quaternion FromToRotation (Vector3 fromDirection, Vector3 toDirection);

描述：创建一个从 fromDirection 旋转到 toDirection 的旋转。

通常情况下，您使用该方法对变换进行旋转，使其的一个轴（例如 Y 轴）跟随世界空间中的目标方向 /toDirection/。

效果等价于Quaternion.SetFromToRotation

(3)Quaternion.AngleAxis

public static Quaternion AngleAxis (float angle, Vector3 axis);

描述：创建一个围绕 axis 旋转 angle 度的旋转。

下面是实现绕着世界Y轴自转的小案例

    private void Update(){transform.rotation=Quaternion.AngleAxis(Time.deltaTime*60,Vector3.up);}

效果预览：

操作旋转:

(4)Quaternion.Slerp

public static Quaternion Slerp (Quaternion a, Quaternion b, float t);

描述：在四元数 a 与 b 之间按比率 t 进行球形插值。参数 t 限制在范围 [0, 1] 内。

(5)Quaternion.RotateTowards

public static Quaternion RotateTowards (Quaternion from, Quaternion to, float maxDegreesDelta);

描述：将 from 四元数朝 to 旋转 maxDegreesDelta 的角度步长（但请注意，该旋转不会过冲）。如果 maxDegreesDelta 为负值，则向远离 to 的方向旋转，直到旋转恰好为相反的方向。

与Quaternion.FromToRotation的区别：

RotateTowards是操作旋转，就是一点点的把from插值到to。而FromToRotation它代表的是一个完整的旋转过程，你需要提供一个起始旋转和目标旋转，方法将返回一个表示从起始方向到目标方向的旋转。

3.刚体旋转系列

(1)Rigidbody.MoveRotation

public void MoveRotation (Quaternion rot);

刚体插值在渲染的任意中间帧中的两个旋转之间平滑过渡，方法必须写在FixedUpdate,参数是四元数。相比于其他所有的旋转方式，他可以实现带动在平台上的物体一起旋转。

实现带动效果：旋转物的刚体必须要勾选isKinematic，切记。

代码如下：

    public float speed;private float angle;private Rigidbody rb;private void Start(){rb = GetComponent<Rigidbody>();}private void FixedUpdate(){angle = Time.fixedDeltaTime * speed;rb.MoveRotation(rb.rotation*Quaternion.Euler(Vector3.up*angle));}

(2)Rigidbody角速度angularVelocity

描述：表示刚体的角速度，即物体绕其自身轴旋转的速度。它是一个三维矢量，每个分量分别表示绕相应轴的旋转速度。

    private void Update(){//绕y轴匀速运动rb.angularVelocity = new Vector3(0, 3, 0);}

它也可以带动平台上的物体一起跟着旋转。

使用角速度需要注意的是，不能勾选isKinematic。

官方说不建议直接修改angularVelocity，会造成失真。但我没遇到过什么问题，我的理解是直接修改内部属性不太符合编程习惯，会破坏完整性。

参考链接：学习笔记3 - 简书