1696. 跳跃游戏 VI
给你一个下标从0开始的整数数组nums和一个整数k。
一开始你在下标 0处。每一步,你最多可以往前跳k步,但你不能跳出数组的边界。也就是说,你可以从下标 i 跳到[i + 1, min(n - 1, i + k)]包含 两个端点的任意位置。
你的目标是到达数组最后一个位置(下标为n - 1),你的 得分 为经过的所有数字之和。
请你返回你能得到的 最大得分 。
示例 1:
输入:nums = [1,-1,-2,4,-7,3], k = 2
输出:7
解释:你可以选择子序列 [1,-1,4,3] (上面加粗的数字),和为 7 。
示例 2:
输入:nums = [10,-5,-2,4,0,3], k = 3
输出:17
解释:你可以选择子序列 [10,4,3] (上面加粗数字),和为 17 。
示例 3:
输入:nums = [1,-5,-20,4,-1,3,-6,-3], k = 2
输出:0
题目分析
经典动态规划问题,更多案例可见 Leetcode 动态规划详解
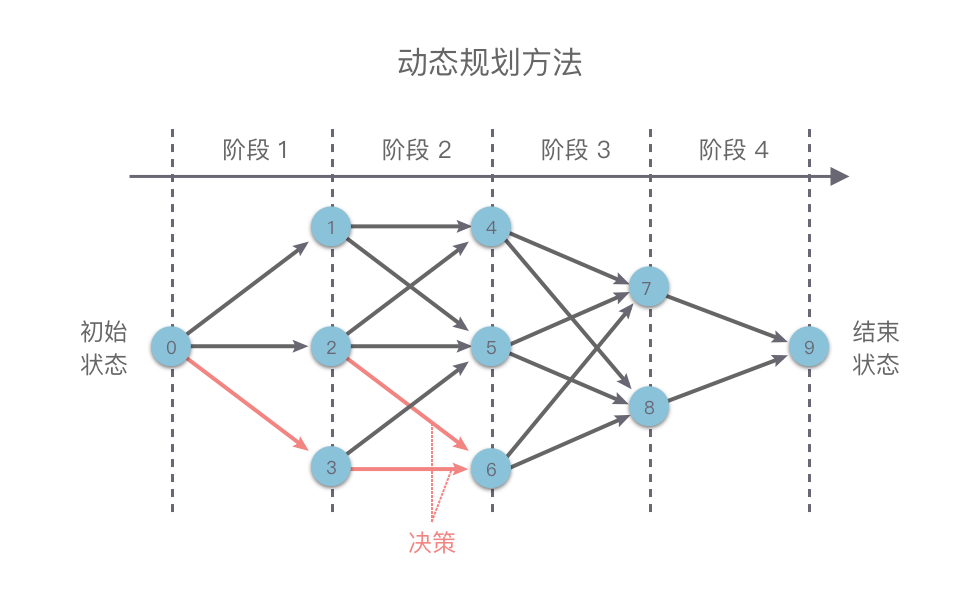
每一个位置的最大值取决于前面 k 步的最大得分,再加上当前位置的得分。我们可以使用动态规划解决本题,解题思路:
- 状态定义:
dp[i]为到达位置 i 的最大得分 - 状态转移方程:枚举 x
- 不偷窃第x间房屋,则总金额为 偷窃前x - 1间的最高总金额
- 偷窃第x间,则总金额为 偷窃前x - 2间最高总金额 + 第x间的金额
d p [ i ] = m a x ( d p [ j ] ) , m a x ( 0 , i − k ) ≤ j < i dp[i] = max(dp[j]), max(0, i − k) ≤ j < i dp[i]=max(dp[j]),max(0,i−k)≤j<i
其中前 k 步的最大值,使用优先队列可以达到 O(nlogn) 的时间复杂度,使用双端队列可以达到 O(n) 的时间复杂度。
此处使用双端队列,对于位置 i ,非前 k 步的队首元素出队,比当前最大值小的队尾元素出队,从而构造了一个队首元素为最大值的单调递减队列
- 初始状态
dp[0] = nums[0],最终答案为dp[n - 1]
动态规划一般用于求解具有重叠子问题和最优子结构的问题,例如最长公共子序列、背包问题、最短路径等。重叠子问题指的是在求解问题的过程中,多次用到相同的子问题,最优子结构指的是问题的最优解可以通过子问题的最优解来构造
class Solution {public int maxResult(int[] nums, int k) {int n = nums.length;int[] dp = new int[n];dp[0] = nums[0];// 双端队列,构造了一个队首元素为最大值的单调递减队列Deque<Integer> queue = new ArrayDeque<>();queue.offerLast(0);for (int i = 1; i < n; i++) {// 不能跳跃到当前格的队首元素出队while (queue.peekFirst() < i - k) {queue.pollFirst();}dp[i] = dp[queue.peekFirst()] + nums[i];// 比当前最大值小的队尾元素出队while (!queue.isEmpty() && dp[queue.peekLast()] <= dp[i]) {queue.pollLast();}queue.offerLast(i);}return dp[n - 1];}
}