线性表是数据结构中最简单、最常用的一种结构,它是由一组具有相同数据类型的元素组成的数据集合。线性表中的元素之间存在顺序关系,每个元素都有一个前驱元素和一个后继元素,除了第一个元素没有前驱元素,最后一个元素没有后继元素。
线性表有两种常见的实现方式:顺序存储和链式存储。
顺序存储:线性表的元素在内存中连续存储,可以使用数组来实现。通过数组的索引来访问元素,插入和删除元素时需要移动其他元素。顺序存储的优点是访问元素快速,缺点是插入和删除元素的操作比较耗时。

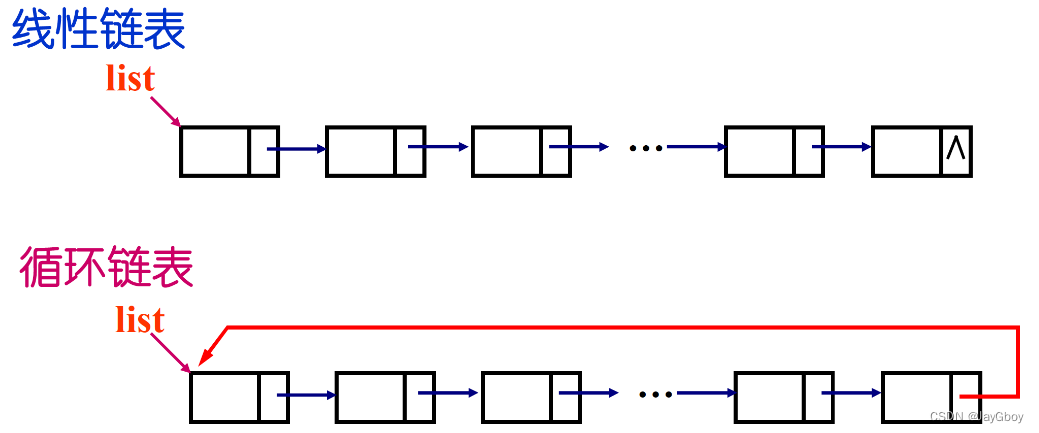
链式存储:线性表的元素在内存中不一定连续存储,每个元素都包含一个数据域和一个指针域,指针域指向下一个元素的地址。通过指针的链接来访问元素,插入和删除元素时只需要修改指针的指向,不需要移动其他元素。链式存储的优点是插入和删除元素的操作比较高效,缺点是访问元素的效率较低。
线性表的常见操作包括:
- 初始化线性表
- 判断线性表是否为空
- 获取线性表的长度
- 获取线性表中某个位置的元素
- 在线性表的某个位置插入元素
- 删除线性表中某个位置的元素
- 查找线性表中某个元素的位置
- 清空线性表
以下是线性表基本操作的代码:
# 初始化线性表
def init_list():list = [] # 使用数组来表示线性表return list# 判断线性表是否为空
def is_empty(list):return len(list) == 0# 获取线性表的长度
def get_length(list):return len(list)# 获取线性表中某个位置的元素
def get_element(list, index):if index < 0 or index >= len(list):return Nonereturn list[index]# 在线性表的某个位置插入元素
def insert_element(list, index, element):if index < 0 or index > len(list):return Falselist.insert(index, element)return True# 删除线性表中某个位置的元素
def delete_element(list, index):if index < 0 or index >= len(list):return Falselist.pop(index)return True# 查找线性表中某个元素的位置
def find_element(list, element):for i in range(len(list)):if list[i] == element:return ireturn -1# 清空线性表
def clear_list(list):list.clear()线性表在实际应用中非常广泛,例如数组、链表、栈、队列等都是线性表的特殊形式。