本专栏内容为：算法学习专栏，分为优选算法专栏，贪心算法专栏，动态规划专栏以及递归，搜索与回溯算法专栏四部分。 通过本专栏的深入学习，你可以了解并掌握算法。

💓博主csdn个人主页：小小unicorn
⏩专栏分类：动态规划专栏
🚚代码仓库：小小unicorn的代码仓库🚚
🌹🌹🌹关注我带你学习编程知识

题目一来源

本题来源为：

Leetcode152. 乘积最大子数组

题目一描述

给你一个整数数组 nums ，请你找出数组中乘积最大的非空连续子数组（该子数组中至少包含一个数字），并返回该子数组所对应的乘积。

测试用例的答案是一个 32-位 整数。

子数组 是数组的连续子序列。

算法原理

1.状态表示

经验+题目要求

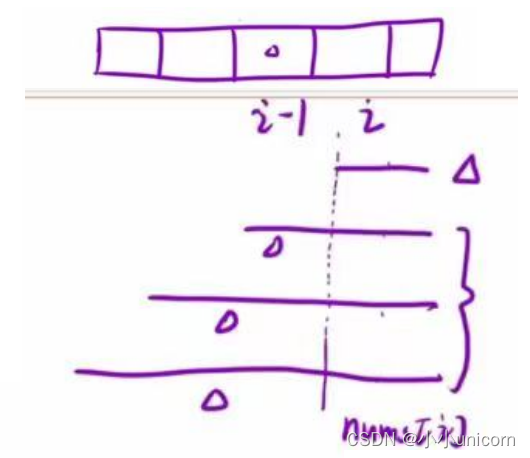
对于本题而言就是：

f[i]表示：以i位置为结尾时的所有子数组中的最大乘积
g[i]表示：以i位置为结尾时的所有子数组中的最小乘积

2.状态转移方程

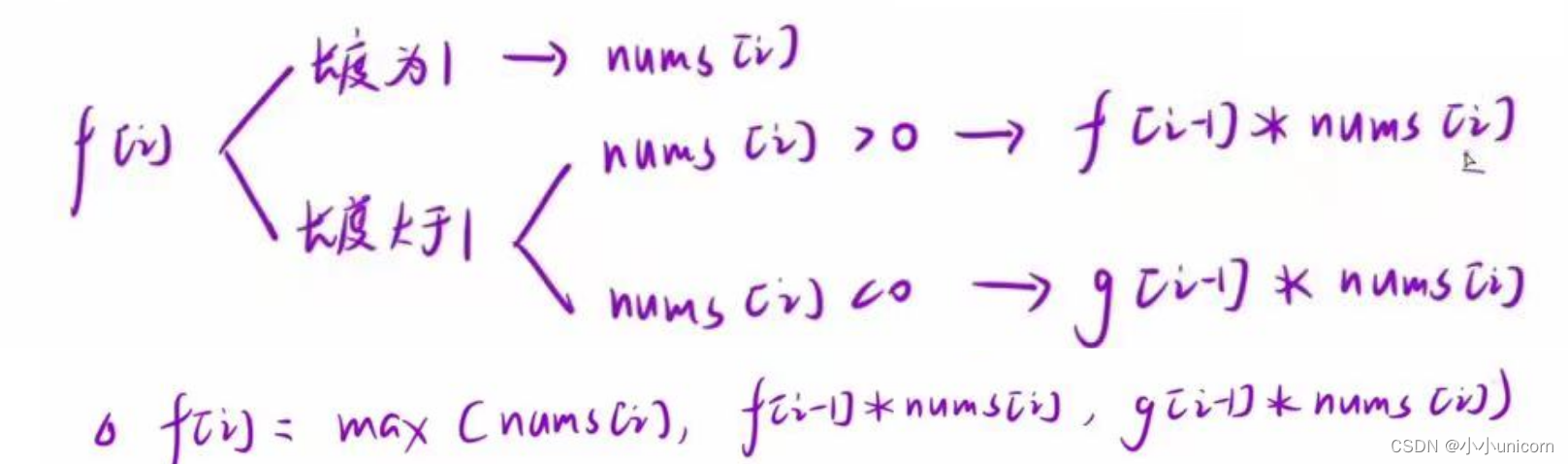
因此状态方程为：

int x=nums[i-1];
int y=f[i-1] * nums[i-1];
int z=g[i-1]* nums[i -1];
f[i]= max(x,max(y,z));
g[i]=min(x,min(y,z));
ret=max(ret,f[i]);

3.初始化

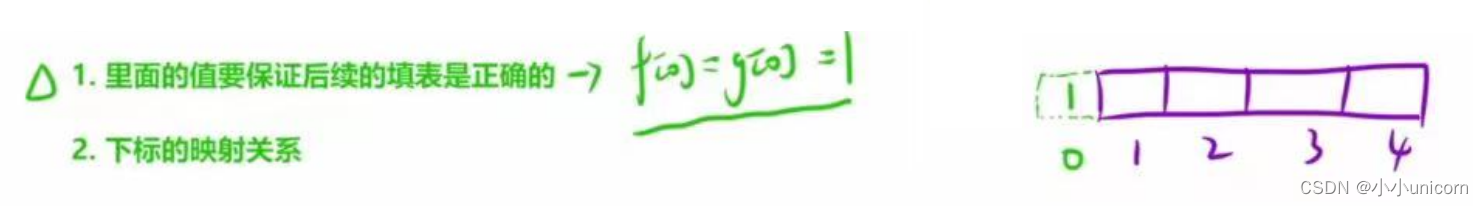
4.填表顺序

从左往右，两个表一起填

5.返回值

f表里的最大值

代码实现

动态规划的代码基本就是固定的四步：

1.创建dp表
2.初始化
3.填表
4.返回值

本题完整代码实现：

class Solution 
{
public:int maxProduct(vector<int>& nums) {//创建dp表int n=nums.size();vector<int> f(n+1);vector<int> g(n+1);//初始化f[0]=g[0]=1;//填表int ret=INT_MIN;for(int i=1;i<=n;i++){int x=nums[i-1];int y=f[i-1] * nums[i-1];int z=g[i-1]* nums[i -1];f[i]= max(x,max(y,z));g[i]=min(x,min(y,z));ret=max(ret,f[i]);}//返回值return ret;}
};

题目二来源

本题来源为：

Leetcode1567. 乘积为正数的最长子数组长度

题目二描述

给你一个整数数组 nums ，请你求出乘积为正数的最长子数组的长度。

一个数组的子数组是由原数组中零个或者更多个连续数字组成的数组。

请你返回乘积为正数的最长子数组长度。

算法原理

1.状态表示

经验+题目要求

对于本题而言就是：

f[i]表示：以i位置为结尾时的所有子数组中的乘积为正数的最长长度
g[i]表示：以i位置为结尾时的所有子数组中的乘积负数的最长长度

2.状态转移方程

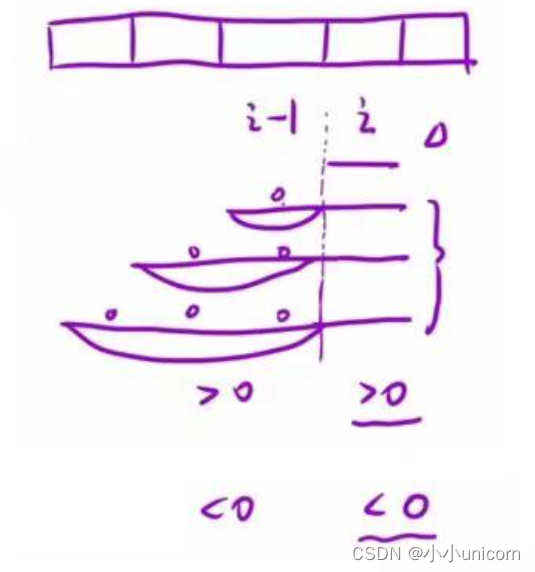
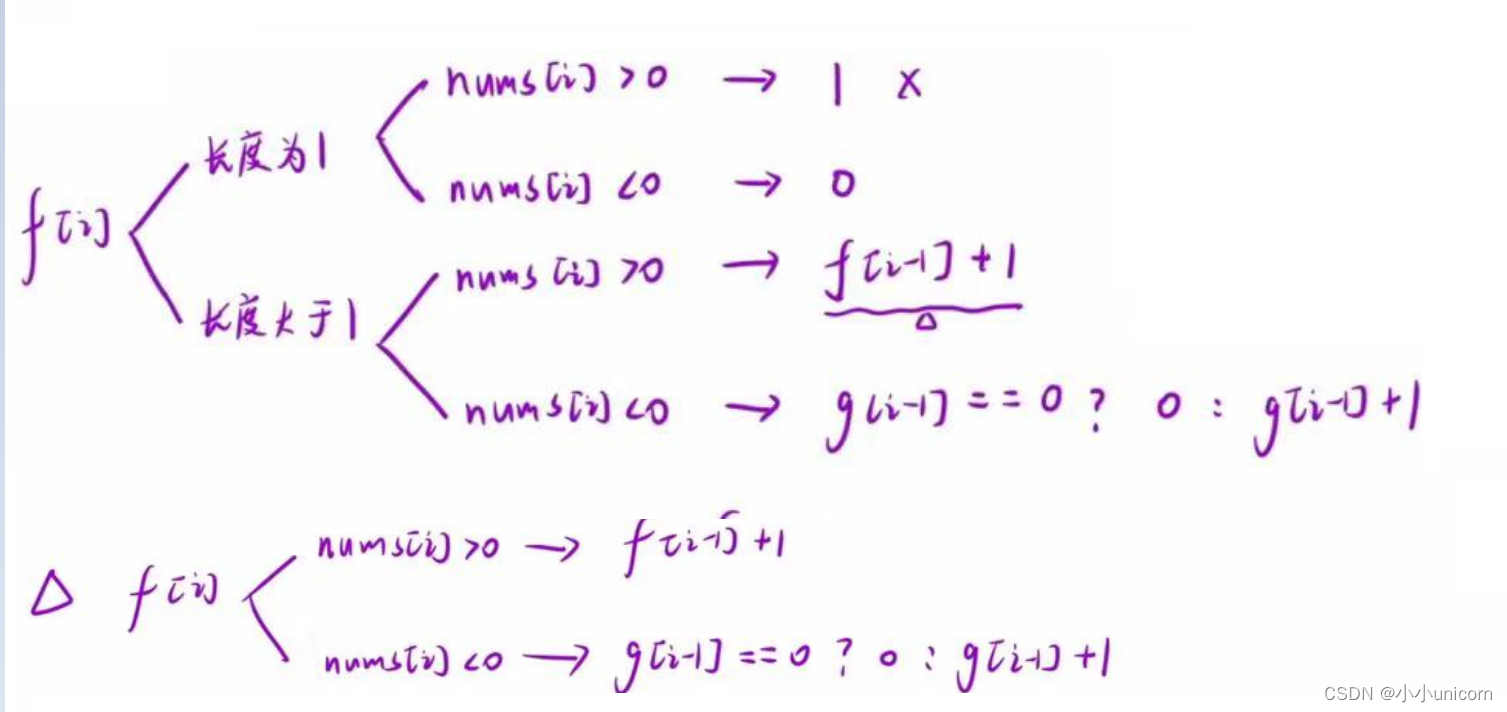
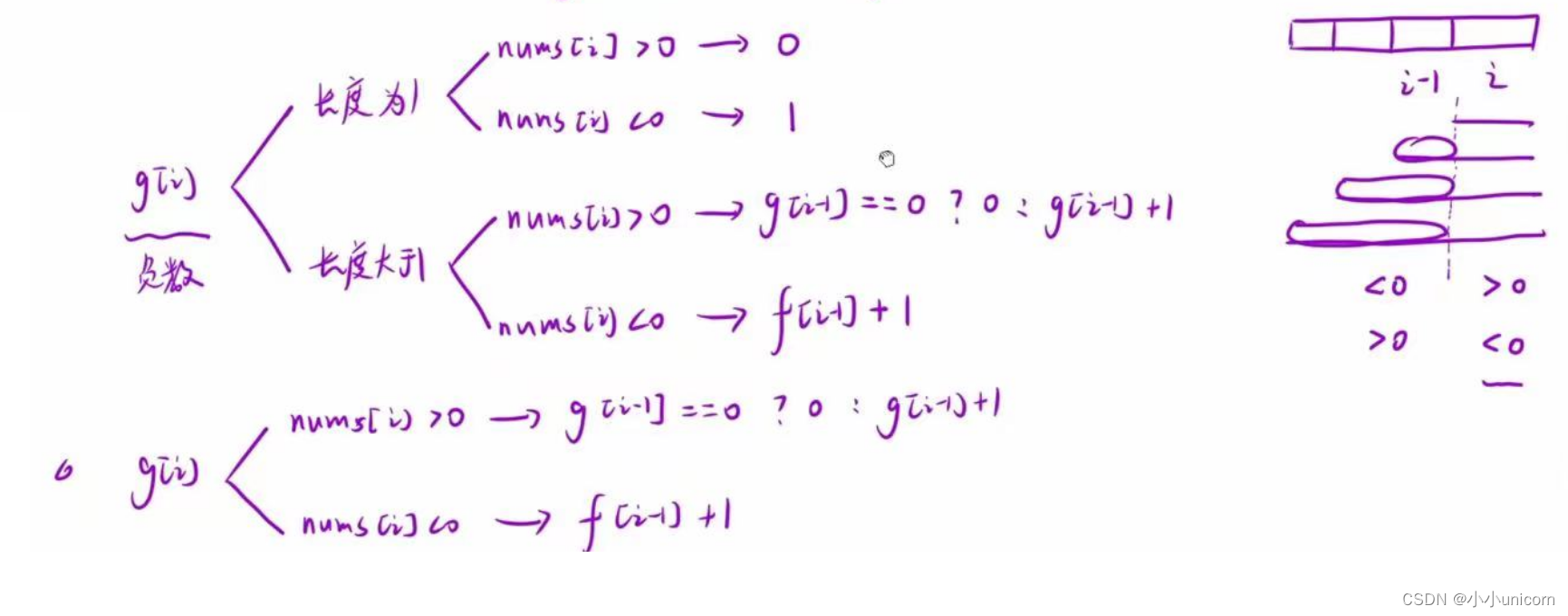
因此状态方程为：

  if(nums[i-1]>0){f[i]= f[i - 1]+ 1;g[i]=g[i-1]==0?0:g[i-1]+1;}else if(nums[i-1]<0){f[i]=g[i-1]==0?0:g[i-1]+ 1;g[i]= f[i - 1]+ 1;}
ret=max(ret,f[i]);

3.初始化

4.填表顺序

从左往右，两个表一起填

5.返回值

f表里面的最大值

代码实现

动态规划的代码基本就是固定的四步：

1.创建dp表
2.初始化
3.填表
4.返回值

本题完整代码实现：

class Solution 
{
public:int getMaxLen(vector<int>& nums) {int n=nums.size();//创建dp表vector<int> f(n+1);vector<int> g(n+1);int ret=INT_MIN;//填表for(int i=1;i<=n;i++){if(nums[i-1]>0){f[i]= f[i - 1]+ 1;g[i]=g[i-1]==0?0:g[i-1]+1;}else if(nums[i-1]<0){f[i]=g[i-1]==0?0:g[i-1]+ 1;g[i]= f[i - 1]+ 1;}ret=max(ret,f[i]);}//返回值return ret;}
};