堆结构的实现和应用

堆结构的实现和应用

    • 1. 堆结构的代码实现
    • 2. 向上调整算法和向下调整算法时间复杂度
    • 3. 堆排序
      • 3.1 方法一
      • 3.2 方法二
      • 3.3 建堆时间复杂度
    • 4. TOP-K问题

1. 堆结构的代码实现

首先，我们先定义一个堆的结构，这里和顺序表的结构一样

typedef int HPDataType;typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;

初始化堆

void HeapInit(HP* hp)
{hp->a = NULL;hp->capacity = 0;hp->size = 0;
}

销毁堆

void HeapDestroy(HP* hp)
{free(hp->a);hp->a = NULL;hp->size = 0;hp->capacity = 0;
}

因为堆的空间是动态开辟的，所以在堆使用结束后，需要把动态开辟的空间释放，避免造成内存泄漏。

堆的插入

在堆尾插入数据后并不能保证插入之后的数据是堆，所以，在插入之后，要进行向上调整算法，直到满足堆。

void HeapPush(HP* hp, HPDataType x)
{assert(hp);HeapCheckCapacity(hp);hp->a[hp->size] = x;hp->size++;HeapUp(hp->a, hp->size - 1);
}

这里也可以不把扩容的代码单独写成一个函数，因为这里只有这一个地方会用到扩容操作，但是还是建议封装成一个函数，一方面可以提高代码的可读性，另一方面平时我们写代码的时候这个操作一般都是封装成一个函数，所以这样写可以在一定程度上避免代码出错。

检查是否需要扩容

void HeapCheckCapacity(HP* hp)
{if (hp->size == hp->capacity){int newcapacity = hp->capacity == 0 ? 4 : hp->capacity * 2;HPDataType* ptr = (HPDataType*)realloc(hp->a, sizeof(HPDataType) * newcapacity);if (ptr == NULL){perror("realloc fail");return NULL;}hp->a = ptr;hp->capacity = newcapacity;}
}

向上调整算法

要求插入之前这个数组是大堆或者小堆，如果时小堆，当插入的孩子比父亲小就交换，直到孩子等于0，即没有父亲的时候交换结束。

算法思想（小堆）：

  1. 将目标节点与父节点比较。
  2. 如果目标节点的值比父节点的值小，则交换目标节点与父节点的位置，并把父节点当作新的目标节点继续向上交换，当目标节点的值比父亲节点大，或者目标节点变成根节点，则停止交换，此时，数组就可以看作一个小堆了。

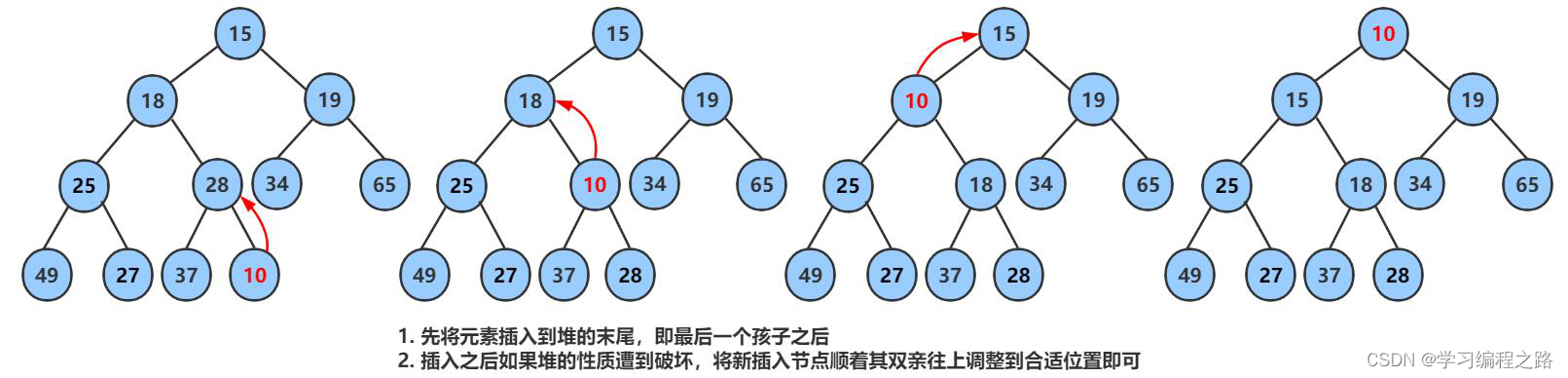
在这里插入图片描述

//假如是小堆
void AdjustUp(HPDataType* a, int child)
{while (child > 0)//调整到根节点处停止{int parent = (child - 1) / 2;if (a[child] < a[parent])//当孩子比父亲小就交换{HPDataType tmp = a[child];a[child] = a[parent];a[parent] = tmp;}else//如果孩子比父亲大就变成堆了，停止交换。{break;}}
}

堆的删除

删除堆是删除堆顶的数据，因为删除堆尾的数据意义不大

  1. 挪动覆盖删除堆顶元素，重新建堆。
    挪动覆盖，不能保证还是堆，父子关系全乱了，只能重新建堆，代价太大。
  2. 将堆顶的数据根最后一个数据一换，然后删除数组最后一个数据，再进行向下调整算法。
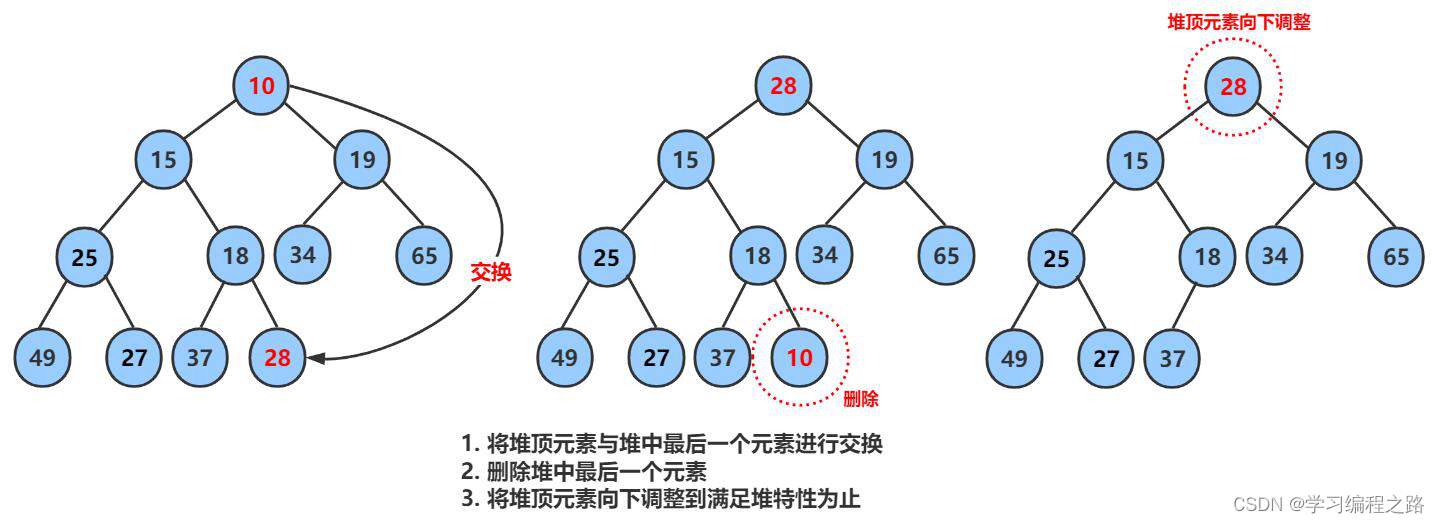
    在这里插入图片描述
void HeapPop(HP* hp)
{assert(hp);assert(!HeapEmpty(hp));Swap(&hp->a[0], &hp->a[hp->size - 1]);hp->size--;AdjustDown(hp->a,hp->size,0);
}

注意：堆为空的时候不能删除

向下调整算法

算法思想（小堆）：

  1. 从根节点开始，选出左右孩子中值较小的孩子
  2. 如果较小的孩子的值比父节点的值小，则交换该孩子节点与父节点的位置，并把该孩子点当作新的父亲节点继续向下交换，当较小孩子节点的值比父亲节点大，或者孩子节点出了数据有效范围，则停止交换，此时，数组就可以看作一个小堆了。

向下调整算法有一个前提：左右子树必须是一个堆，才能调整。
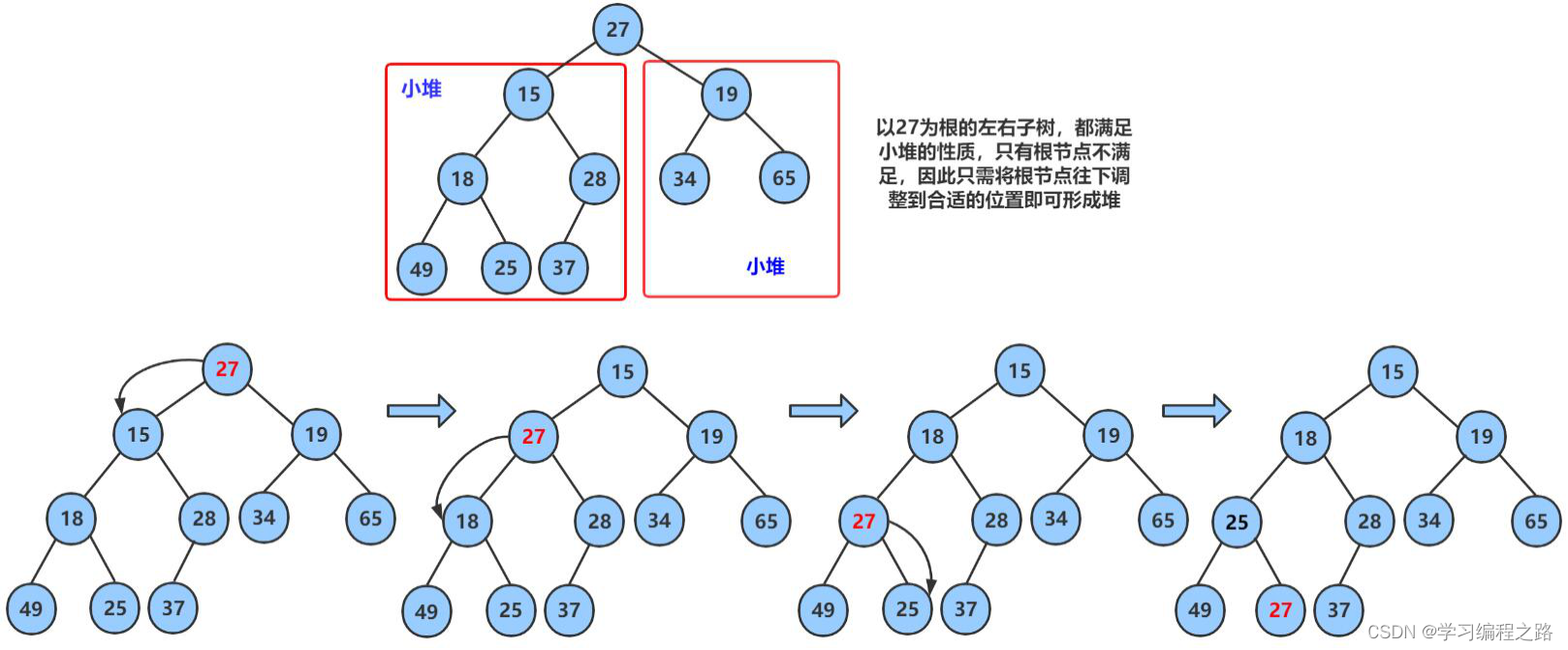
在这里插入图片描述

代码如下：

void AdjustDown(HPDataType* a, int n, int parent)
{int child = parent * 2 + 1;//假设左孩子小while (child < n){//如果有右孩子并且右孩子比左孩子小,假设不成立if (child + 1 < n && a[child + 1] < a[child]){child++;//如果假设不成立，把较小孩子改为有孩子}if (a[child] < a[parent])//当较小的孩子比父亲小，则交换{Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;//当较小的孩子比父亲大，则停止交换}}
}

交换元素

因为多处需要用到交换函数，所以我们单独封装成一个函数

void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}

取出堆顶元素

HPDataType HeapTop(HP* hp)
{assert(hp);assert(!HeapEmpty(hp));return hp->a[0];
}

检测堆是否为空，如果为空返回非零结果，如果不为空返回0

bool HeapEmpty(HP* hp)
{return hp->size == 0;
}

获取堆中有效元素个数

int HeapSize(HP* hp)
{assert(hp);return hp->size;
}

全部代码实现
Heap.h

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <assert.h>typedef int HPDataType;typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;void HeapInit(HP* hp);void HeapDestroy(HP* hp);void HeapPush(HP* hp,HPDataType x);void HeapPop(HP* hp);HPDataType HeapTop(HP * hp);bool HeapEmpty(HP* hp);int HeapSize(HP* hp);

Heap.c

#include "Heap.h"void HeapInit(HP* hp)
{assert(hp);hp->a = NULL;hp->capacity = 0;hp->size = 0;
}void HeapDestroy(HP* hp)
{assert(hp);free(hp->a);hp->a = NULL;hp->capacity = 0;hp->size = 0;
}void HeapCheckCapacity(HP* hp)
{assert(hp);if (hp->size == hp->capacity){int newcapacity = hp->capacity == 0 ? 4 : hp->capacity * 2;HPDataType* ptr = (HPDataType*)realloc(hp->a, sizeof(HPDataType) * newcapacity);if (ptr == NULL){perror("realloc fail");exit(-1);}hp->a = ptr;hp->capacity = newcapacity;}
}void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}void AdjustUp(HPDataType* a, int child)
{while (child > 0){int parent = (child - 1) / 2;if (a[child] < a[parent]){Swap(&a[child], &a[parent]);}else{break;}child = parent;}
}void HeapPush(HP* hp, HPDataType x)
{assert(hp);HeapCheckCapacity(hp);hp->a[hp->size] = x;hp->size++;AdjustUp(hp->a, hp->size - 1);
}void AdjustDown(HPDataType* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){if (child + 1 < n && a[child + 1] < a[child]){child++;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}bool HeapEmpty(HP* hp)
{return hp->size == 0;
}void HeapPop(HP* hp)
{assert(hp);assert(!HeapEmpty(hp));Swap(&hp->a[0], &hp->a[hp->size - 1]);hp->size--;AdjustDown(hp->a,hp->size,0);
}HPDataType HeapTop(HP* hp)
{assert(hp);assert(!HeapEmpty(hp));return hp->a[0];
}int HeapSize(HP* hp)
{assert(hp);return hp->size;
}

Test.c

#include "Heap.h"int main()
{HP hp;HeapInit(&hp);int a[] = { 65,100,70,32,50,60 };int sz = sizeof(a) / sizeof(a[0]);int i = 0;for (i = 0; i < sz; i++){HeapPush(&hp, a[i]);}for (i = 0; i < sz; i++){printf("%d\n", HeapTop(&hp));HeapPop(&hp);}HeapDestroy(&hp);return 0;
}

运行结果如图：
在这里插入图片描述
这里只是把数据从小到大打印出来，并没有改变数组的内容，所以不是堆排序。

2. 向上调整算法和向下调整算法时间复杂度

假如树的高度为h，那么向上调整算法和向下调整算法，调整的次数最多为h-1次，也可以认为h次，因为，我们之前已经推出高度h和节点个数N的关系，那么我们很容易推导处下图的公式。

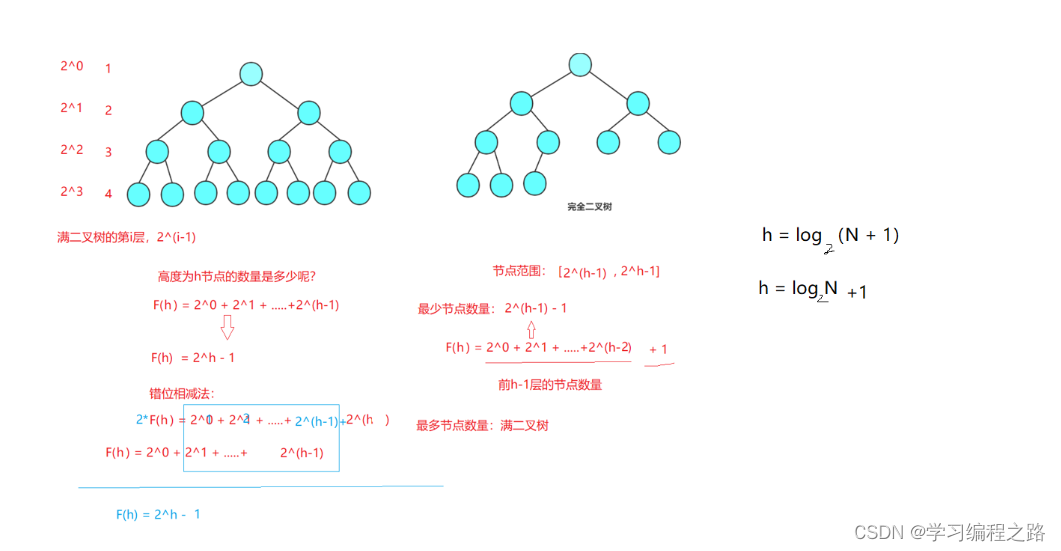
在这里插入图片描述

所以，向上调整算法和向下调整算法时间复杂度用大O的渐进法表示就是O(logN)。

3. 堆排序

3.1 方法一

#include "Heap.h"void HeapSort(int* a, int n)
{HP hp;HeapInit(&hp);int i = 0;for (i = 0; i < n; i++){HeapPush(&hp, a[i]);}i = 0;while (!HeapEmpty(&hp)){int top = HeapTop(&hp);a[i++] = top;HeapPop(&hp);}HeapDestroy(&hp);
}int main()
{int a[] = { 3,5,1,4 };int sz = sizeof(a) / sizeof(a[0]);HeapSort(a, sz);int i = 0;for (i = 0; i < sz; i++){printf("%d ", a[i]);}return 0;
}

运行结果如图：
在这里插入图片描述
这样虽然也可以实现堆排序，但是有弊端：必须先有一个堆，太麻烦，需要拷贝数据空间复制度比较高。

3.2 方法二

  1. 利用数组进行向上调整建堆或向上调整建堆的方法进行建堆。
  2. 小堆，选出最小的，首尾交换，最小的放到最后的位置，把最后一个数据，不看作堆里面的，向下调整后就可以选出次小的，最终，排出来的数据就是降序。

向上调整建堆：

void HeapSort(int* a, int n)
{//O(N * log(N))//建堆 -- 向上调整建堆int i = 0;for (i = 1; i < n; i++){// 升序 -- 建大堆// 降序 -- 建小堆AdjustUp(a, i);}O(N * logN)int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);//在调整，选出次小的数AdjustDown(a, end, 0);end--;}
}int main()
{int a[] = { 3,5,1,4 };int sz = sizeof(a) / sizeof(a[0]);HeapSort(a, sz);int i = 0;for (i = 0; i < sz; i++){printf("%d ", a[i]);}return 0;
}

运行结果如图：
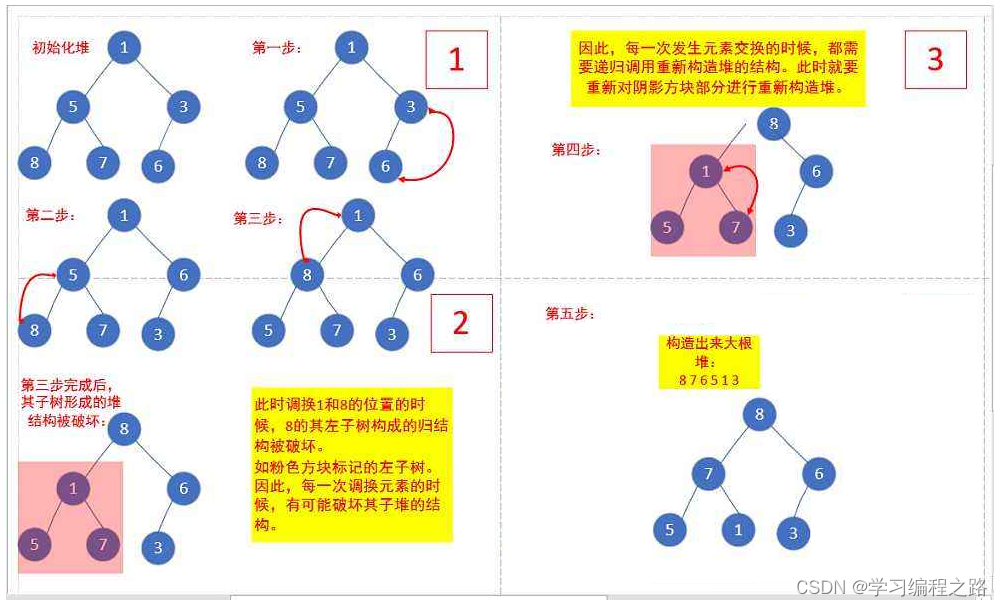
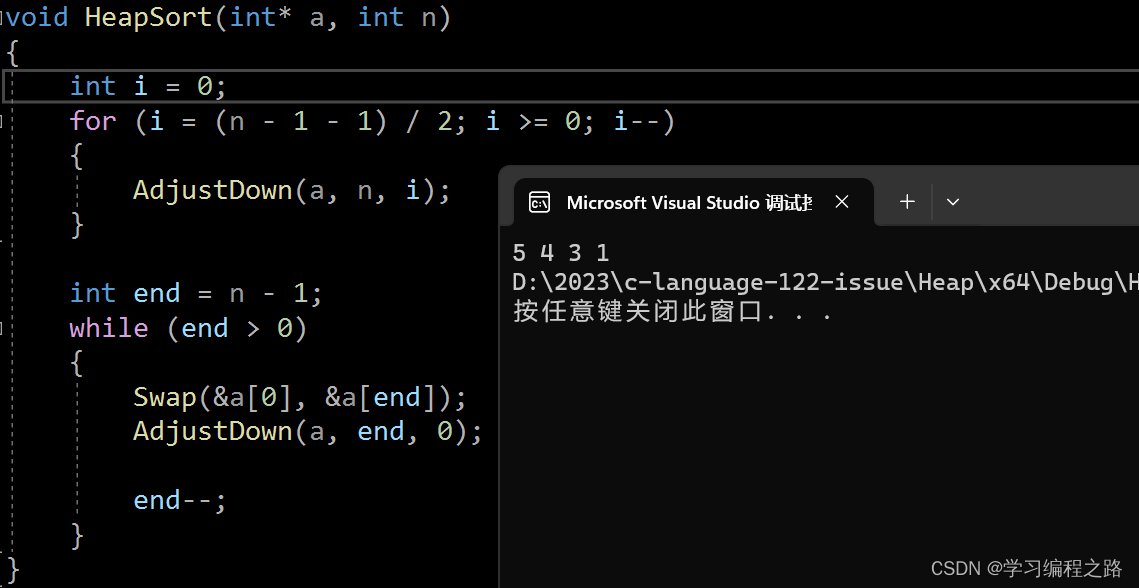
在这里插入图片描述

向下调整建堆
在这里插入图片描述

void HeapSort(int* a, int n)
{//O(N)int i = 0;for (i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(a, n, i);}O(N * logN)int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);end--;}
}int main()
{int a[] = { 3,5,1,4 };int sz = sizeof(a) / sizeof(a[0]);HeapSort(a, sz);int i = 0;for (i = 0; i < sz; i++){printf("%d ", a[i]);}return 0;
}

运行结果如图：
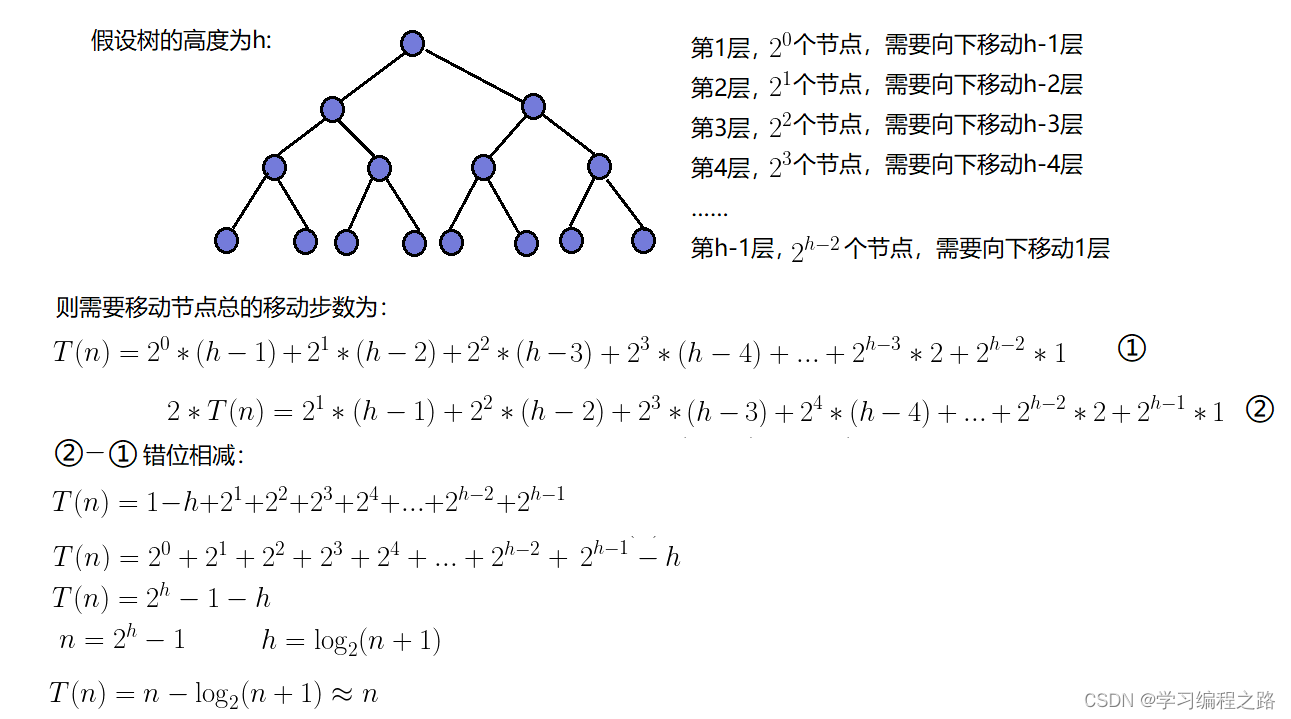
在这里插入图片描述

3.3 建堆时间复杂度

因为堆是完全二叉树，而满二叉树也是完全二叉树，此处为了简化使用满二叉树来证明(时间复杂度本来看的就是近似值，多几个节点不影响最终结果)：

在这里插入图片描述

4. TOP-K问题

TOP-K问题：即求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。

比如：专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。

对于Top-K问题，能想到的最简单直接的方式就是排序，但是：如果数据量非常大，排序就不太可取了(可能数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决，基本思路如下：

  1. 用数据集合中前K个元素来建堆
    • 前k个最大的元素，则建小堆
    • 前k个最小的元素，则建大堆
  2. 用剩余的N-K个元素依次与堆顶元素来比较，不满足则替换堆顶元素

将剩余N-K个元素依次与堆顶元素比完之后，堆中剩余的K个元素就是所求的前K个最小或者最大的元素。

#include <stdio.h>
#include <stdlib.h>
#include <time.h>void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}void AdjustDown(int* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){if (child + 1 < n && a[child] > a[child + 1]){child++;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}void CreateNDate()
{// 造数据int n = 100;srand(time(NULL));const char* file = "data.txt";FILE* fin = fopen(file, "w");if (fin == NULL){perror("fopen error");return;}for (size_t i = 0; i < n; ++i){int x = rand() % 100;fprintf(fin, "%d\n", x);}fclose(fin);
}void PrintTopK(int k)
{const char* file = "data.txt";FILE* fout = fopen(file, "r");if (fout == NULL){perror("fopen error");return;}int* kminheap = (int*)malloc(sizeof(int) * k);if (kminheap == NULL){perror("malloc error");return;}for (int i = 0; i < k; i++){fscanf(fout, "%d", &kminheap[i]);}// 建小堆for (int i = (k - 1 - 1) / 2; i >= 0; i--){AdjustDown(kminheap, k, i);}int val = 0;while (!feof(fout)){fscanf(fout, "%d", &val);if (val > kminheap[0]){kminheap[0] = val;AdjustDown(kminheap, k, 0);}}for (int i = 0; i < k; i++){printf("%d ", kminheap[i]);}printf("\n");
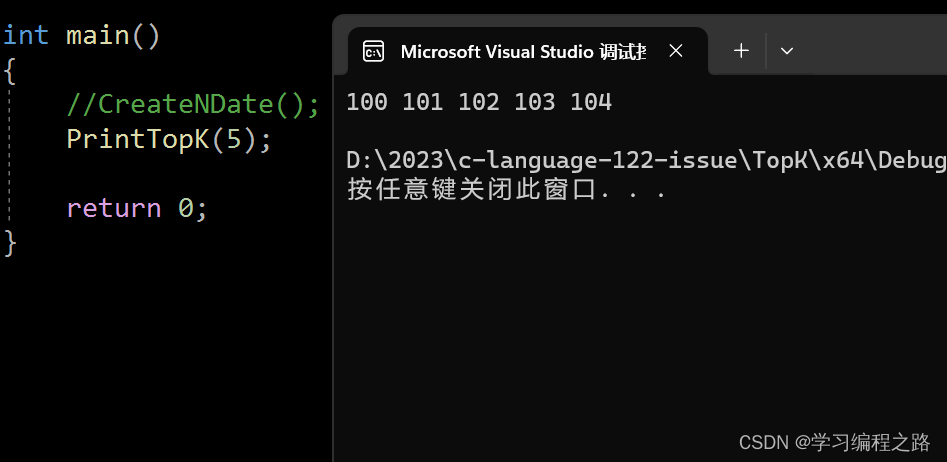
}int main()
{//CreateNDate();PrintTopK(5);return 0;
}

我们创造好文件之后可以，可以手动修改文件内容。

在这里插入图片描述

运行结果如图：
在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/485035.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

Java项目：23 基于SSM实现的在线购物商城系统

Java项目：23 基于SSM实现的在线购物商城系统

作者主页&#xff1a;舒克日记 简介&#xff1a;Java领域优质创作者、Java项目、学习资料、技术互助 文中获取源码 项目介绍 这是一个基于ssm框架的购物系统 该项目中有五个子模块。shop-manager模块负责导入该项目所需要的所有依赖包。shop-web模块负责存放前端代码以及项目…
阅读更多...
机器人内部传感器阅读笔记及心得-位置传感器-电位器式位置传感器

机器人内部传感器阅读笔记及心得-位置传感器-电位器式位置传感器

位置传感器 位置感觉是机器人最基本的感觉要求&#xff0c;可以通过多种传感器来实现。位置传感器包括位置和角度检测传感器。常用的机器人位置传感器有电位器式、光电式、电感式、电容式、霍尔元件式、磁栅式及机械式位置传感器等。机器人各关节和连杆的运动定位精度要求、重…
阅读更多...
[力扣 Hot100]Day31 K 个一组翻转链表

[力扣 Hot100]Day31 K 个一组翻转链表

题目描述 给你链表的头节点 head &#xff0c;每 k 个节点一组进行翻转&#xff0c;请你返回修改后的链表。 k 是一个正整数&#xff0c;它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍&#xff0c;那么请将最后剩余的节点保持原有顺序。 你不能只是单纯的改变节点…
阅读更多...
charles-mock数据

charles-mock数据

1、通过Charles抓包&#xff0c;找到需要mock的接口&#xff0c;把返回的结果保存到本地。 路径&#xff1a;接口选中-右键保存&#xff08;save Response&#xff09; 2、打开保存的文件&#xff0c;文件返回的结果/结构改成自己想要的模式&#xff0c;改好后保存文件 3、选中…
阅读更多...
RM电控讲义【HAL库篇】

RM电控讲义【HAL库篇】

这段代码中do while的作用&#xff1a; 宏定义中的语句块&#xff1a;do { ... } while (0) 允许你在宏定义中创建一个语句块&#xff0c;从而可以包含多条语句。这在宏定义中特别有用&#xff0c;因为宏只是简单的文本替换&#xff0c;不像函数那样有作用域和返回类型。因此&…
阅读更多...
电阻知识详解

电阻知识详解

基本介绍 电阻阻碍电流流动&#xff1a;只要有电流流过电阻&#xff0c;就会产生功率损耗 基本单位&#xff1a;欧姆&#xff0c;Ω 换算单位&#xff1a;微欧&#xff08;uΩ&#xff09;、毫欧&#xff08;mΩ&#xff09;、千欧&#xff08;kΩ&#xff09;、兆欧&#x…
阅读更多...
YOLO v9 出世！

YOLO v9 出世！

当今的深度学习方法专注于如何设计最合适的目标函数&#xff0c;以使模型的预测结果能够尽可能地接近真实值。同时&#xff0c;还需要设计一种适当的架构&#xff0c;以便为预测获取足够的信息。现有方法忽略了一个事实&#xff0c;即当输入数据经过逐层特征提取和空间转换时&a…
阅读更多...
Linux工具篇Vim

Linux工具篇Vim

分享Linux的一些基础的工具&#xff0c;今天分享的就是Linux下的vim&#xff0c;vim其实是一个编辑器。我们可以理解为Windows下的一个记事本。 这个是vim的键盘图。 Linux编辑器-vim使用 vi/vim 的区别简单点来说&#xff0c;它们都是多模式编辑器&#xff0c;不同的是 vim 是…
阅读更多...
前端基础自学整理｜DOM树

前端基础自学整理｜DOM树

DOM&#xff0c;文档对象模型&#xff08;Document Object Model&#xff09;&#xff0c;简单的说&#xff0c;DOM是一种理念&#xff0c;一种思想&#xff0c;一个与系统平台和编程语言无关的接口&#xff0c;一种方法, 使 Web开发人员可以访问HTML元素&#xff01;不是具体方…
阅读更多...
K8S故障处理指南：网络问题排查思路

K8S故障处理指南：网络问题排查思路

1. 前言 对于私有化环境&#xff0c;客户的网络架构&#xff0c;使用的云平台存在着各种差异&#xff0c;K8S网络可能会出现各种问题&#xff0c;此文着重讲解遇到此种问题的排查方法和思路&#xff0c;不会涉及相关网络底层技术描述. 环境说明 由于我们的k8s网络组件默认使…
阅读更多...
gitlab的使用

gitlab的使用

前一篇文章我们已经知道Git人人都是中心&#xff0c;那他们怎么交互数据呢&#xff1f; • 使用GitHub或者码云等公共代码仓库 • 使用GitLab私有仓库 目录 一、安装配置gitlab 安装 初始化 这里初始化完成以后需要记住一个初始密码 查看状态 二、使用浏览器访问&#xf…
阅读更多...
18.贪心算法

18.贪心算法

排序贪心 区间贪心 删数贪心 统计二进制下有多少1 int Getbit_1(int n){int cnt0;while(n){nn&(n-1);cnt;}return cnt; }暴力加一维前缀和优化 #include <iostream> #include <climits> using namespace std; #define int long long const int N2e510; in…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023