R语言实现分位数回归和二次分位数回归-编程知识

R语言实现分位数回归和二次分位数回归

大家好，我是带我去滑雪！新的一年，新的气象，在接下来的日子里我将继续和各位小伙伴们分享我在科研道路上，学习的一些知识！

分位数回归和二次分位数回归是统计学中用于分析因变量与自变量之间关系的方法，特别适用于处理非线性和异方差的情况。在以往的学习中，大家最常用的是分位数回归，也比较容易找到分位数回归的相关R代码，但是在后续的学习中，我发现网上关于二次分位数回归的代码与学习内容比较少，代码难以获取，为了解决这个问题，就有了这一篇博客的由来。

一、认识分位数回归和二次分位数回归

（1）什么是分位数回归？

（2）什么是二次分位数回归？

二、代码实现与实战

（1）下载相关包并导入

（2）导入数据

（3）绘制散点图

（4）验证因变量y是否服从正态分布

（5）分位数回归

（6）二次分位数回归

一、认识分位数回归和二次分位数回归

（1）什么是分位数回归？

分位数回归是一种回归分析方法，它估计的不是依变量的均值，而是给定分位数下的条件分布。通常，我们感兴趣的不仅仅是了解自变量如何影响因变量的期望值，还想了解自变量如何影响因变量在不同分位数下的表现。
分位数回归提供了更全面的关于因变量与自变量之间关系的信息，能够捕捉到数据中存在的各种异质性和非线性关系。

（2）什么是二次分位数回归？

二次分位数回归是分位数回归的一种扩展，它在分位数回归的基础上引入了自变量的平方项或其他高次项。
通过引入二次项，二次分位数回归可以更好地捕捉到因变量和自变量之间的非线性关系。这样的非线性关系可能在特定的分位数下更为显著或重要。
二次分位数回归能够提供更精细的数据拟合，进一步改善了对数据的解释和预测能力。

二、代码实现与实战

（1）下载相关包并导入

install.packages("hrbrthemes")
install.packages("palmerpenguins")
install.packages("ggplot")
library(tidyverse)       
library(ggsci)           
library(ggExtra)         
library(ggpmisc)        
library(palmerpenguins) 
library(ggplot2)
library(quantreg)

（2）导入数据

data<-read.csv("E:/工作/硕士/博客/data.csv",header=TRUE,sep=",",fileEncoding = "GBK")
data

部分数据展示：

x y type
1 13.2567 6.3488 5
2 13.2099 6.2226 5
3 12.8984 6.0332 3
4 12.9607 6.0837 4
5 12.8361 5.8060 5
6 12.8049 5.6924 5
7 12.5245 5.6420 4
8 12.5401 5.6672 5
9 12.2285 5.5031 5
10 11.3718 5.1876 3

（3）绘制散点图

plot(data$x, data$y, xlab='x', ylab='y')
plot(data$x, data$type, xlab='x', ylab='type')

输出结果：

（4）验证因变量y是否服从正态分布

boxplot(data$y, xlab='y')
#简单验证一下因变量y是否服从正态分布
qqnorm(data$y, main='QQ plot')
qqline(data$y, col='red', lwd=2)
attach(data)

输出结果：

（5）分位数回归

rq_result <- rq(x ~ y, tau=c(0.05, 0.25, 0.55, 0.80, 0.99))
summary(rq_result)

输出结果：

Call: rq(formula = x ~ y, tau = c(0.05, 0.25, 0.55, 0.8, 0.99))

tau: [1] 0.05

Coefficients:
coefficients lower bd upper bd
(Intercept) 5.90509 -0.04805 6.97585
y 0.92993 0.69762 1.96490

Call: rq(formula = x ~ y, tau = c(0.05, 0.25, 0.55, 0.8, 0.99))

tau: [1] 0.25

Coefficients:
coefficients lower bd upper bd
(Intercept) 1.95680 0.86718 3.95382
y 1.77132 1.37449 1.98130

Call: rq(formula = x ~ y, tau = c(0.05, 0.25, 0.55, 0.8, 0.99))

tau: [1] 0.55

Coefficients:
coefficients lower bd upper bd
(Intercept) 2.16670 0.54266 2.77642
y 1.77877 1.65164 2.09980

Call: rq(formula = x ~ y, tau = c(0.05, 0.25, 0.55, 0.8, 0.99))

tau: [1] 0.8

Coefficients:
coefficients lower bd upper bd
(Intercept) 2.36689 1.27416 3.19410
y 1.79510 1.63677 1.98807

Call: rq(formula = x ~ y, tau = c(0.05, 0.25, 0.55, 0.8, 0.99))

tau: [1] 0.99

Coefficients:
coefficients lower bd upper bd
(Intercept) 1.78244 -1.46488 6.81231
y 1.97464 1.25385 2.64396

plot(x, y, cex=2, type='n', xlab='x', ylab='y',lty=2,pch=16)
points(x, y, cex=2, col='blACK',pch=16)
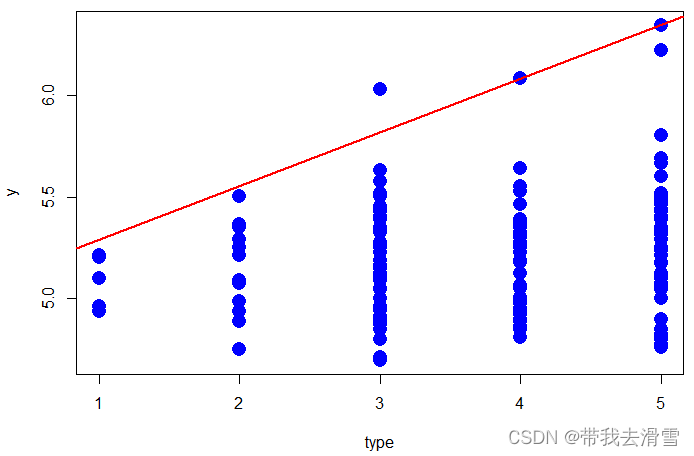
abline(rq(y~x, tau=0.99), col='red',lty=1,lwd=2)plot(type, y, cex=2, type='n', xlab='type', ylab='y',lty=2,pch=16)
points(type, y, cex=2, col='blue',pch=16)
abline(rq(y~type, tau=0.99), col='red',lty=1,lwd=2)plot(type, y, cex=2, type='n', xlab='type', ylab='y',lty=2,pch=16)
points(type, y, cex=2, col='blue',pch=16)
abline(rq(y~type, tau=0.99), col='red',lty=1,lwd=2)

输出结果：

（6）二次分位数回归


rq_result1 <- lrq(y~A*x+B*x^2+C,start = list(A=0,B=0,C=0),tau=0.99,data=data)
summary(rq_result1 )
summary.nlrq(rq_result1 )
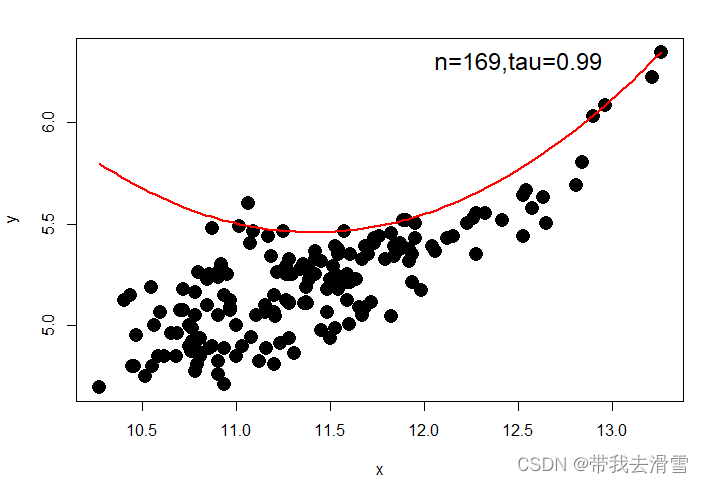
plot(x, y, cex=2, type='n', xlab='x', ylab='y',lty=2,pch=16)
points(x, y, cex=2, col='black',pch=16)curve(-5.96362*x+0.26132*x^2+39.48284, col='red',lty=1,lwd=2, add = TRUE)
text(12.5,6.3,"n=169,tau=0.99",cex=1.5,font=1)

输出结果：