文章目录
- 一、题目
- 二、解法
- 三、完整代码
所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。
一、题目
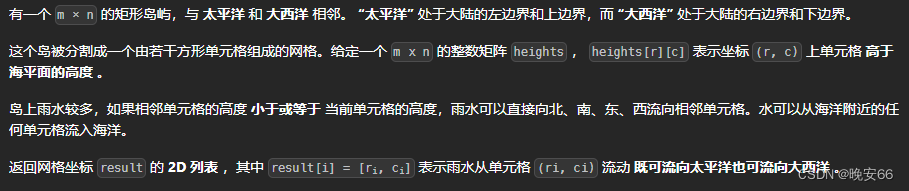
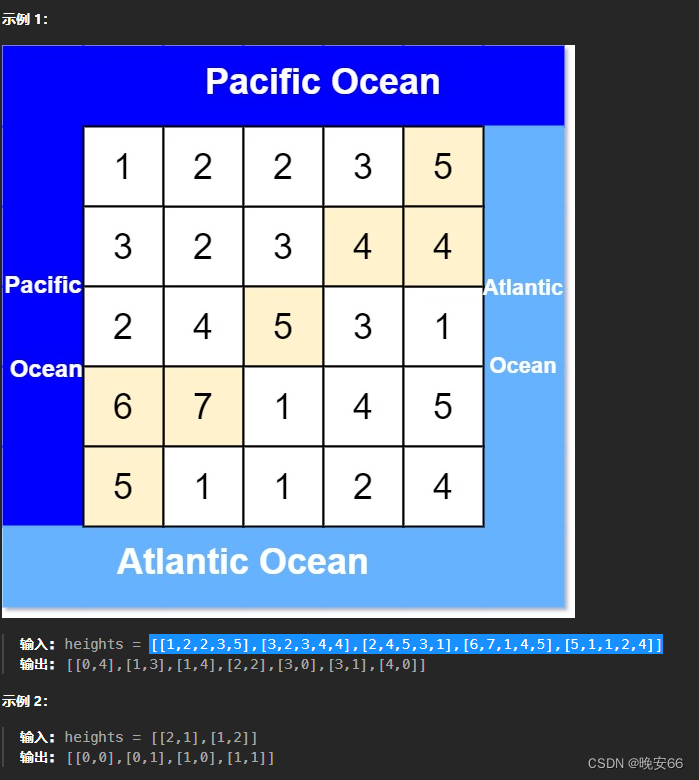
二、解法
思路分析:题目要求雨水既能流向太平洋也能流向大西洋的网格。雨水流向取决于网格的高度。一个比较直接的方式是对每个网格做深度优先搜索,去判断该网格点是否连接太平洋和大西洋,连接的条件就是小于或者等于网格的高度。这样的方法对于当个网格点的复杂度是 O ( m × n ) O(m \times n) O(m×n),一共有 O ( m × n ) O(m \times n) O(m×n)个网格,总的复杂度是 O ( m 2 × n 2 ) O(m^2 \times n^2) O(m2×n2)。这种方法的缺点是没有利用点与点之间的关系,单个网格点的遍历不能再下一次遍历中利用。
为了能充分利用点与点之间的关系,逆向思维一下,顺着雨水流向逆向遍历。从太平洋边上的节点出发,标记所有能流入太平洋的网格点;同样的方法,从大西洋边上的节点出发,标记所有能流入大西洋的的网格点。然后找到同时有太平洋和大西洋标记的节点输出。
程序如下:
// 417、太平洋大西洋水流问题
class Solution {
private:vector<vector<int>> result;vector<vector<int>> delta_x_y = { {0, -1}, {0, 1}, {-1, 0}, {1, 0} }; // 上下左右四个方向的偏移量void dfs(const vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y) { // 1、递归输入参数visited[x][y] = true;// 3、单层递归逻辑for (int i = 0; i < 4; i++) {int nextx = x + delta_x_y[i][0];int nexty = y + delta_x_y[i][1];// 2、终止条件 逆流而上式的遍历 grid[nextx][nexty] < grid[x][y]if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size() || visited[nextx][nexty] || grid[nextx][nexty] < grid[x][y]) continue; dfs(grid, visited, nextx, nexty);}}
public:vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights) {vector<vector<bool>> pacific = vector<vector<bool>>(heights.size(), vector<bool>(heights[0].size(), false)); // 遍历过的坐标vector<vector<bool>> Atlanti = vector<vector<bool>>(heights.size(), vector<bool>(heights[0].size(), false));for (int i = 0; i < heights[0].size(); i++) { // 遍历边界行dfs(heights, pacific, 0, i); // 第一行dfs(heights, Atlanti, heights.size() - 1, i); // 最后一行 }for (int j = 0; j < heights.size(); j++) { // 遍历大西洋的网格点dfs(heights, pacific, j, 0); // 第一列dfs(heights, Atlanti, j, heights[0].size() - 1); // 最后一列 }for (int i = 0; i < heights.size(); i++) { // 遍历行 for (int j = 0; j < heights[0].size(); j++) { // 遍历列if (pacific[i][j] && Atlanti[i][j]) result.push_back({i, j}); // 深度优先搜索,将连接的陆地都标记上true}}return result;}
};
复杂度分析:
- 时间复杂度: O ( m × n ) O(m \times n) O(m×n),其中 m m m和 n n n分别是网格数组的行数和列数。深度优先搜索的时间复杂度为 O ( m × n ) O(m \times n) O(m×n),主程序当中使用了四个for循环,前两个用来遍历边界,后两个用来遍历太平洋和大西洋的标记数组。前两个for循环的时间复杂度不是 O ( m × ( m × n ) + n × ( m × n ) ) = O ( ( m + n ) × ( m × n ) ) O(m \times (m \times n)+n \times (m \times n)) = O((m+n) \times (m \times n)) O(m×(m×n)+n×(m×n))=O((m+n)×(m×n))。因为我们引入了标记数组,标记过的网格不会多次遍历,实际上的复杂度是两个标记数组遍历的复杂度 O ( 2 × ( m × n ) ) O(2 \times (m \times n)) O(2×(m×n)),后两个循环的复杂度也是 O ( m × n ) O(m \times n) O(m×n)。因此总的时间复杂度为 O ( 3 × m × n ) = O ( m × n ) O(3 \times m \times n) = O(m \times n) O(3×m×n)=O(m×n)。
- 空间复杂度: O ( m × n ) O(m \times n) O(m×n)。
三、完整代码
# include <iostream>
# include <vector>
# include <string>
using namespace std;// 417、太平洋大西洋水流问题
class Solution {
private:vector<vector<int>> result;vector<vector<int>> delta_x_y = { {0, -1}, {0, 1}, {-1, 0}, {1, 0} }; // 上下左右四个方向的偏移量void dfs(const vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y) { // 1、递归输入参数visited[x][y] = true;// 3、单层递归逻辑for (int i = 0; i < 4; i++) {int nextx = x + delta_x_y[i][0];int nexty = y + delta_x_y[i][1];// 2、终止条件 逆流而上式的遍历 grid[nextx][nexty] < grid[x][y]if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size() || visited[nextx][nexty] || grid[nextx][nexty] < grid[x][y]) continue; dfs(grid, visited, nextx, nexty);}}
public:vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights) {vector<vector<bool>> pacific = vector<vector<bool>>(heights.size(), vector<bool>(heights[0].size(), false)); // 遍历过的坐标vector<vector<bool>> Atlanti = vector<vector<bool>>(heights.size(), vector<bool>(heights[0].size(), false));for (int i = 0; i < heights[0].size(); i++) { // 遍历边界行dfs(heights, pacific, 0, i); // 第一行dfs(heights, Atlanti, heights.size() - 1, i); // 最后一行 }for (int j = 0; j < heights.size(); j++) { // 遍历大西洋的网格点dfs(heights, pacific, j, 0); // 第一列dfs(heights, Atlanti, j, heights[0].size() - 1); // 最后一列 }for (int i = 0; i < heights.size(); i++) { // 遍历行 for (int j = 0; j < heights[0].size(); j++) { // 遍历列if (pacific[i][j] && Atlanti[i][j]) result.push_back({i, j}); // 深度优先搜索,将连接的陆地都标记上true}}return result;}
}; void my_print(vector<vector<int>> result, string message) {cout << message << endl;for (vector<vector<int>>::iterator it = result.begin(); it != result.end(); it++) {for (vector<int>::iterator jt = (*it).begin(); jt != (*it).end(); jt++) {cout << *jt << " ";}cout << endl;}
}int main() {//vector<vector<int>> heights = { { 1, 2, 2, 3, 5},{3, 2, 3, 4, 4},{2, 4, 5, 3, 1},{6, 7, 1, 4, 5},{5, 1, 1, 2, 4} };//vector<vector<int>> heights = { {1} };vector<vector<int>> heights = { {3,3,3,3,3,3}, {3,0,3,3,0,3 }, {3,3,3,3,3,3} };Solution s1;vector<vector<int>> result = s1.pacificAtlantic(heights);my_print(result, "结果:");system("pause");return 0;
}
end