一、排序的基本概念
1-1、稳定性
稳定性指的是相同的数据所在的位置经过排序后是否发生变化。若是排序后,次序不变,则是稳定的。
1-2、归位
每一趟排序能确定一个元素的最终位置。
1-3、内部排序
排序记录全部存放在内存中进行排序的过程。
1-4、外部排序
待排序记录的数量很大,以至于内存不能容纳全部记录,在排序过程中尚需对外存进行访问的排序过程。
1-5、排序小结(要背)

比较最好时间复杂度,会发现,当待排序的序列基本有序的话,适合采用:
- 直接插入排序
- 希尔排序
- 冒泡排序
二、直接插入排序
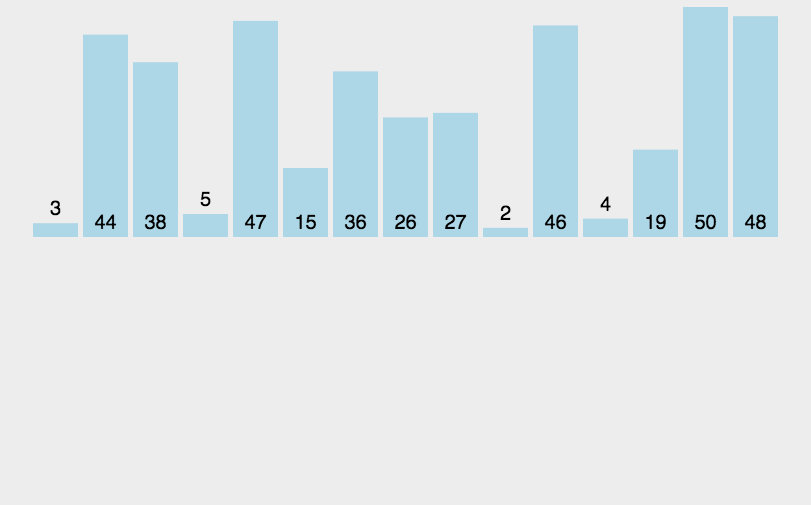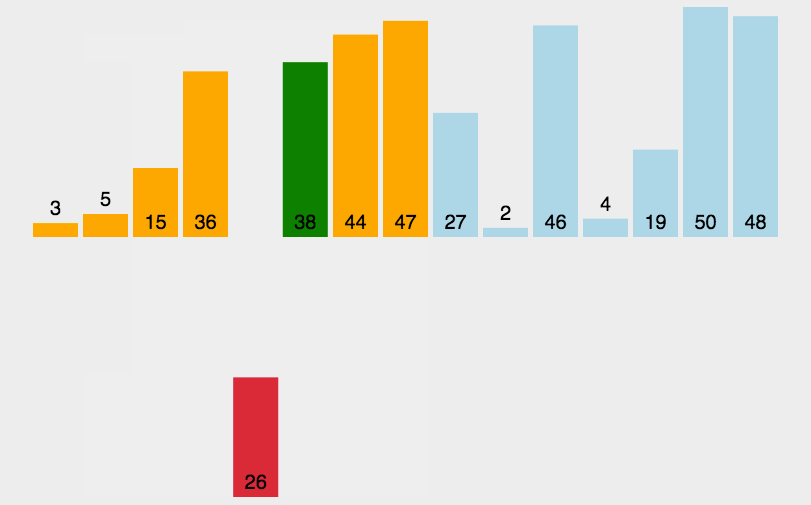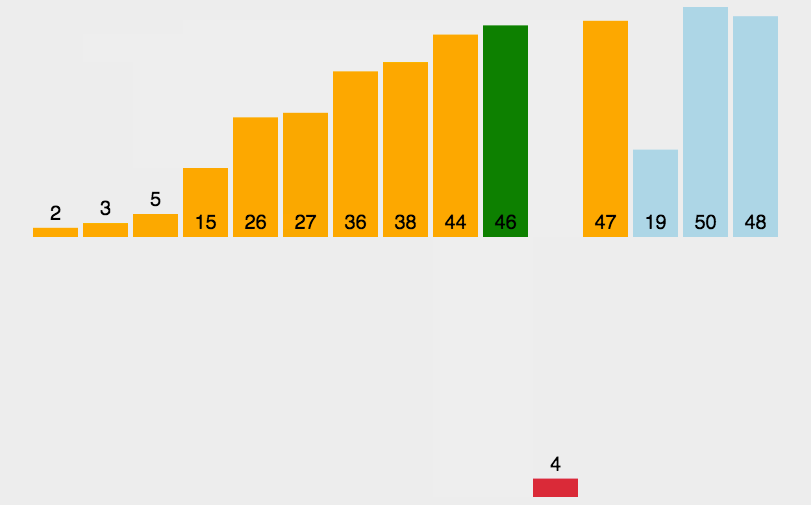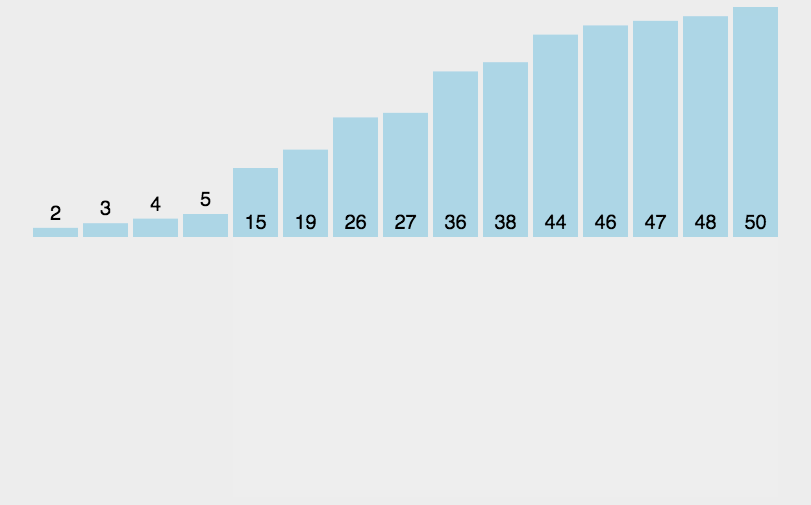
稳定的
不归位

三、希尔排序
直接插入排序的改进。
基本思想:现将整个待排记录序列分割成若干子序列,然后分别进行直接插入排序;待整个序列中的记录基本有序的时候,再对全体记录进行一次直接插入排序。
示例:


不稳定
不归位
四、真题1
真题1:

真题2:
 真题3:
真题3:

真题4:

五、简单选择排序
算法思想:从待排数组中找到最小值,再将最小值与已排好序的数组后一位进行交换。
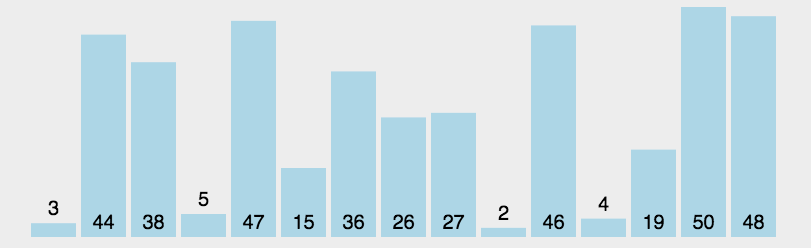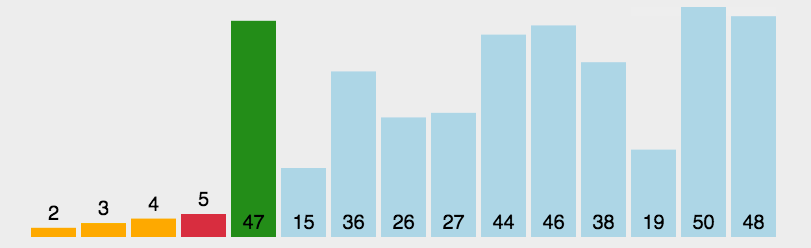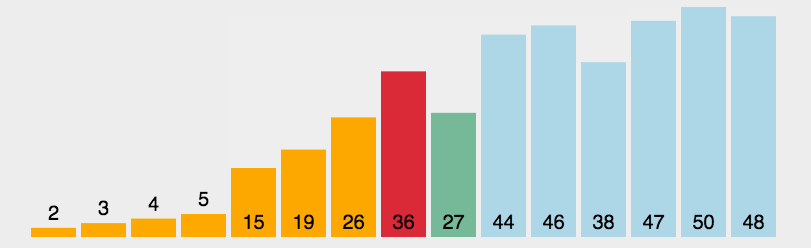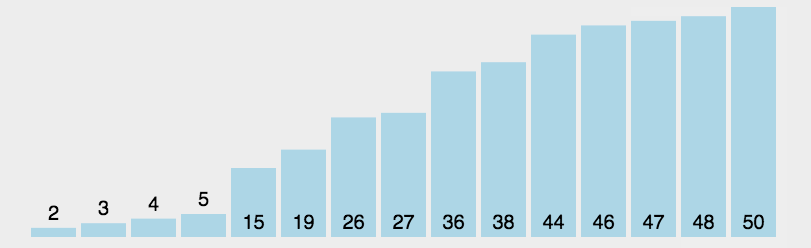
归位
不稳定

六、堆排序(简单了解)
示例:
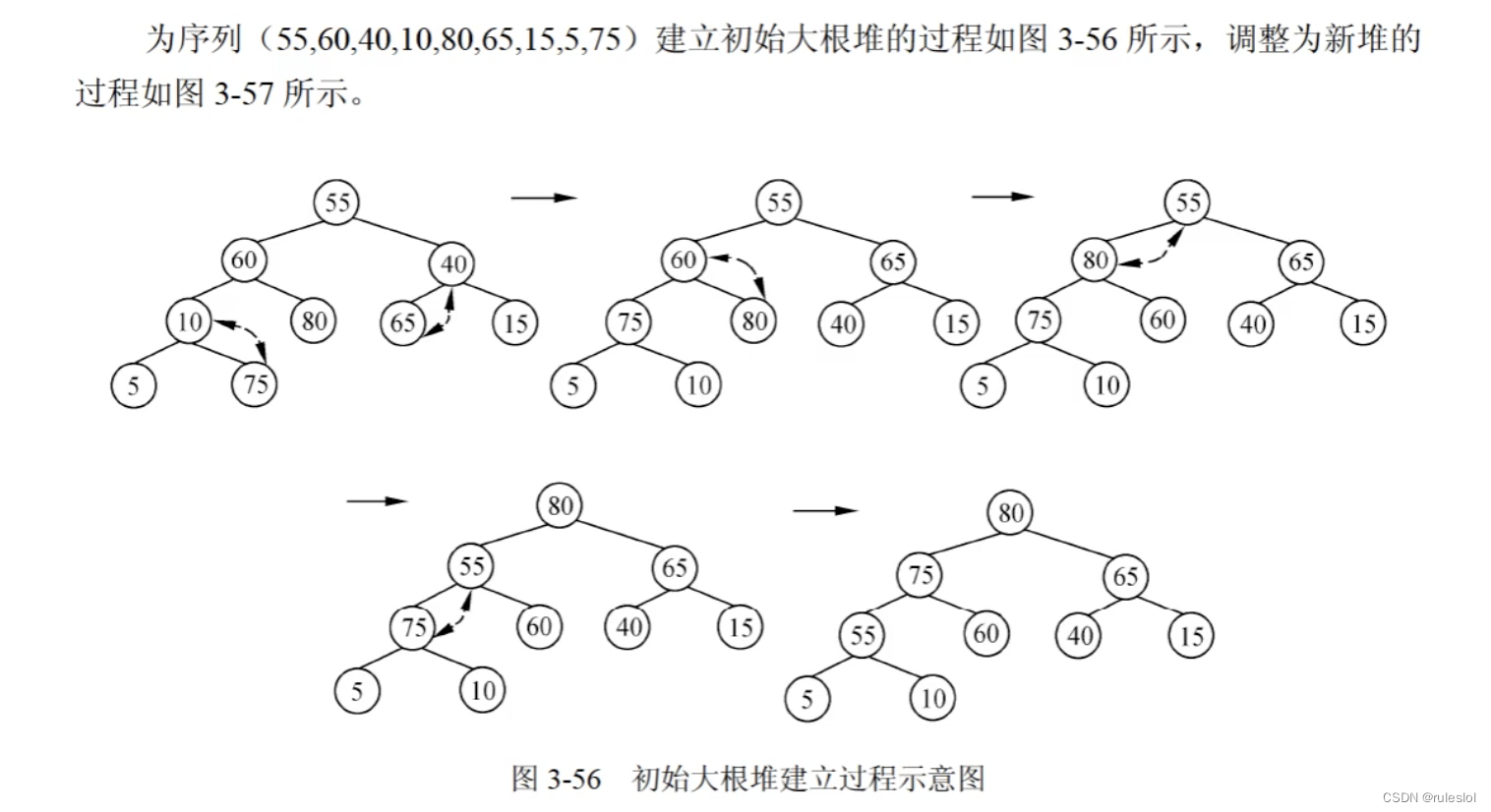

此时,根元素80是最大的元素,将根元素80和队列最后一个元素10交换,并将80脱离当前序列(归位),此时,新的二叉树不满足大顶堆的规则,则继续调整。
每次调整完得到的根节点都是当前序列的最大元素!!!
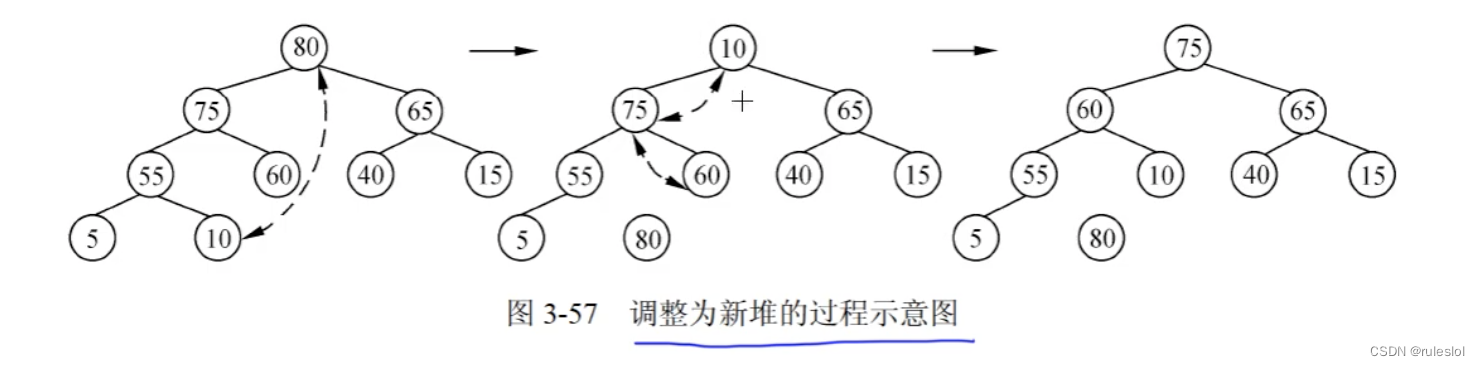
归位
不稳定

七、真题2
真题1:

真题2:

八、冒泡排序
基本思想:相邻两个元素,俩俩交换。
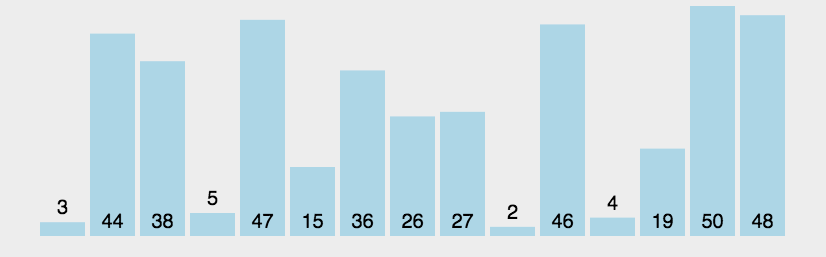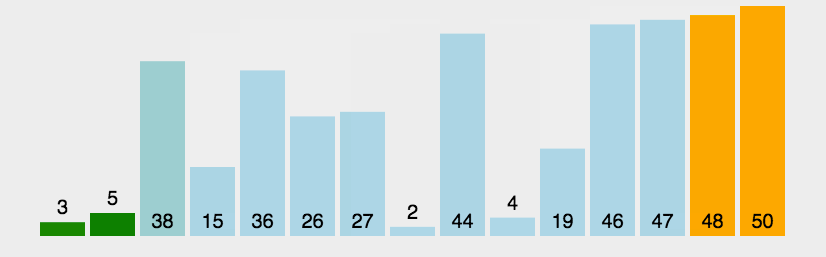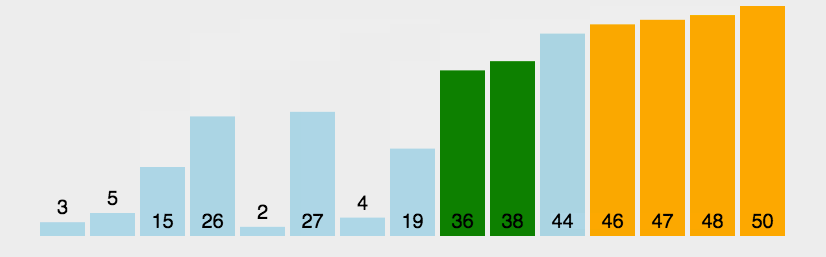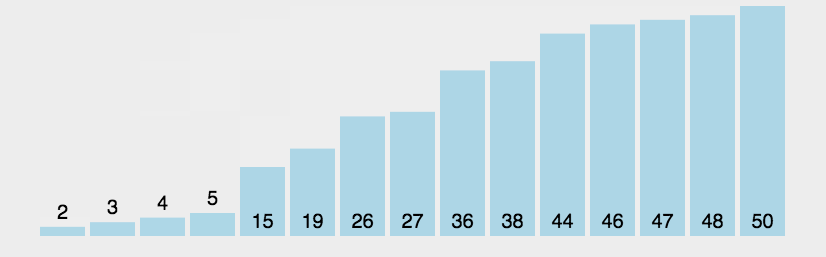

稳定
归位
九、快速排序
快速排序首先选择了一个基准值,然后分别选择两个指针在数组中一个找大,一个找小,然后进行交换。
通过一趟排序将待排序的记录以基准值为分界,分为独立的两个部分,称为前半区和后半区;前半区均小于基准值,后半区均大于基准值。
然后再分别对这两个部分在进行快速排序,从而使得整个序列有序。
分治:分而治之。
归位
不稳定!!!

纠错:空间时间复杂度是:O(log2n);

十、真题2
真题1:

真题2:

真题3:

真题4:

十一、归并排序
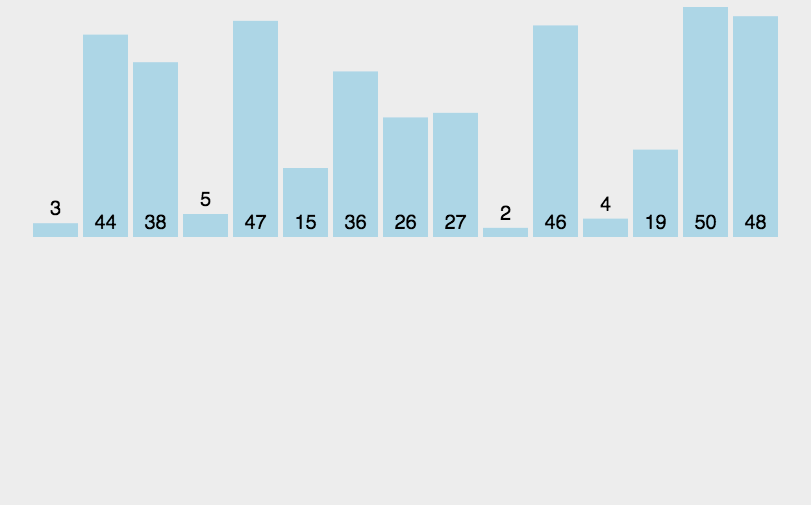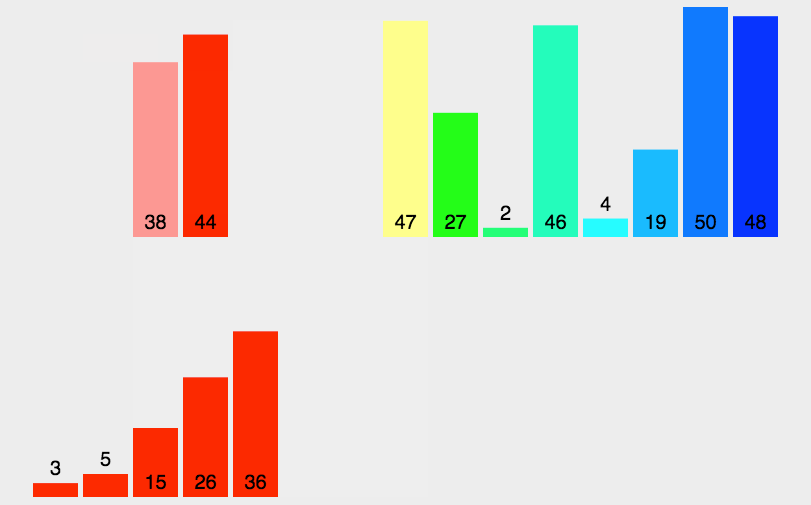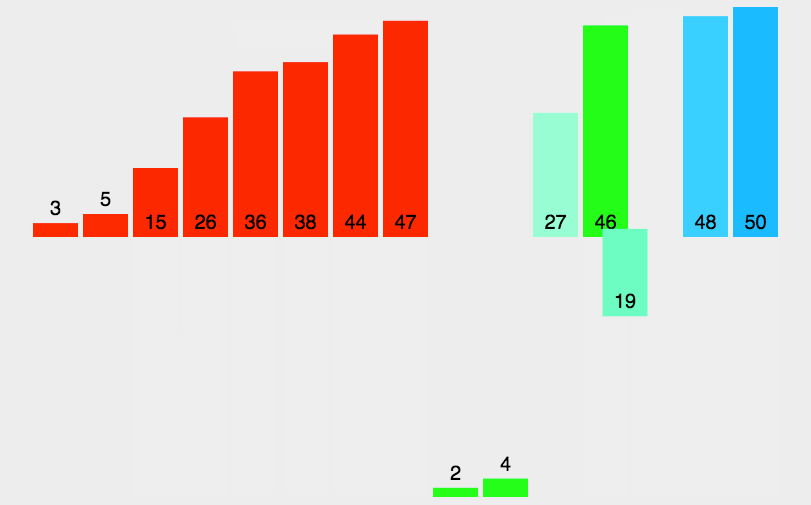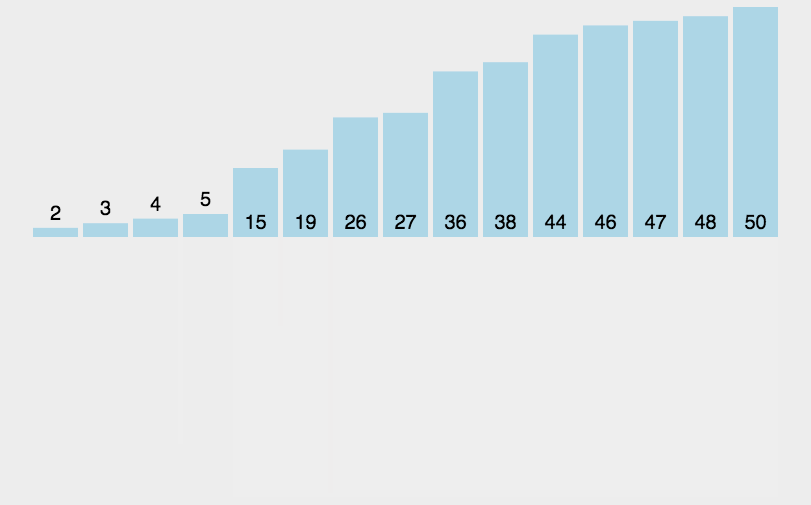
示例:
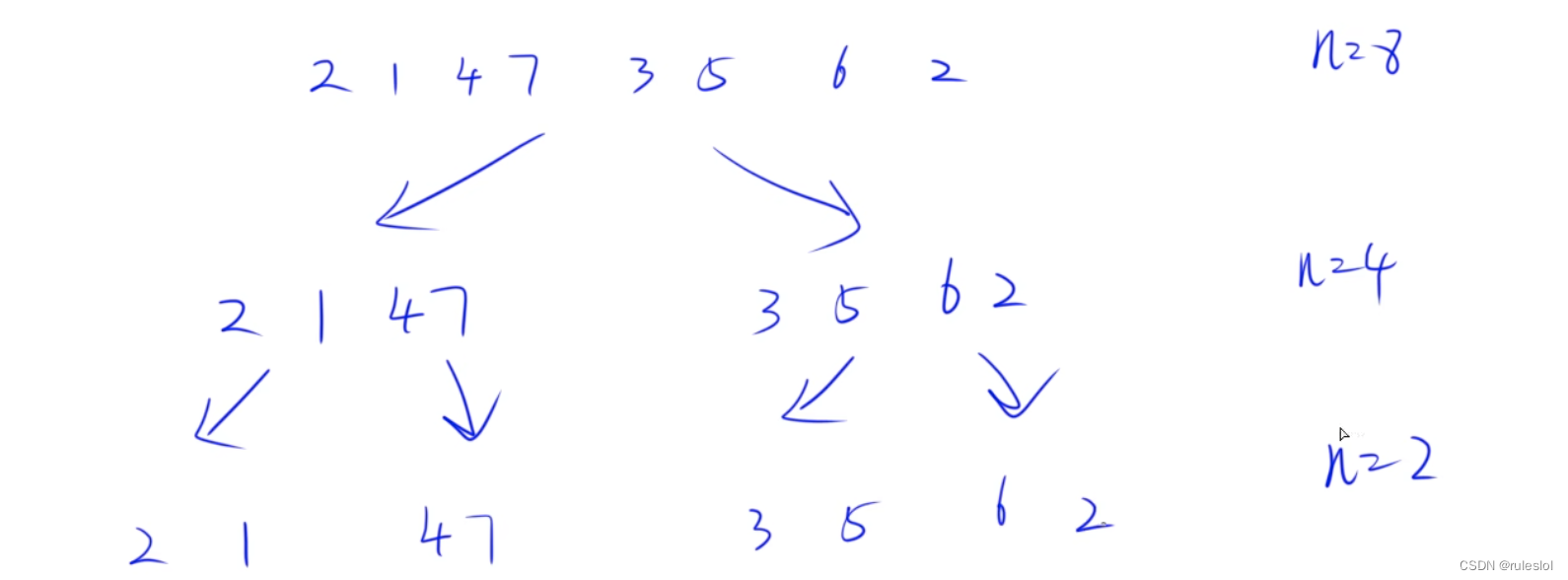
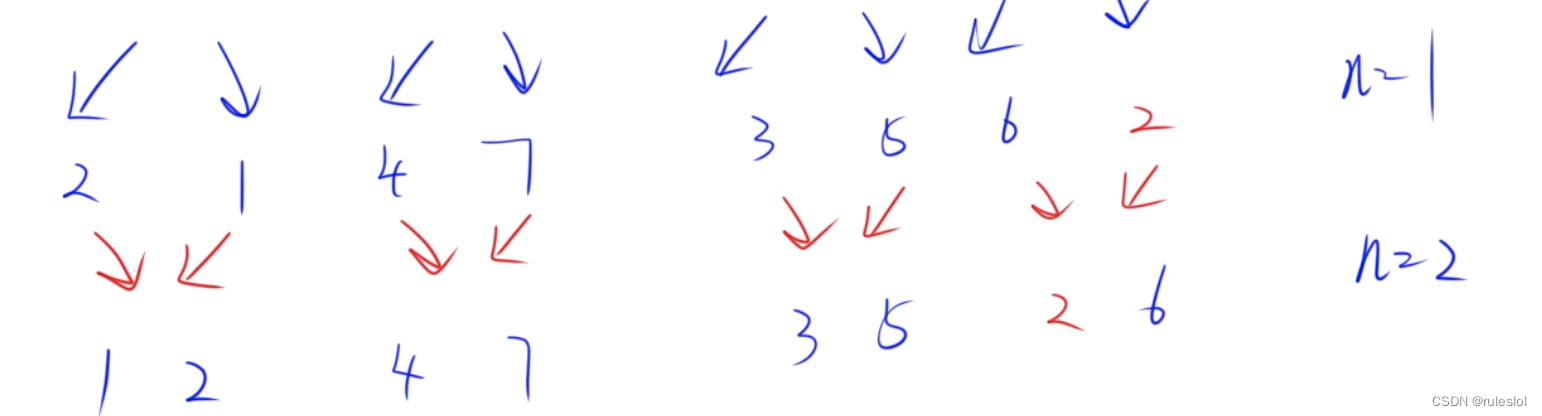
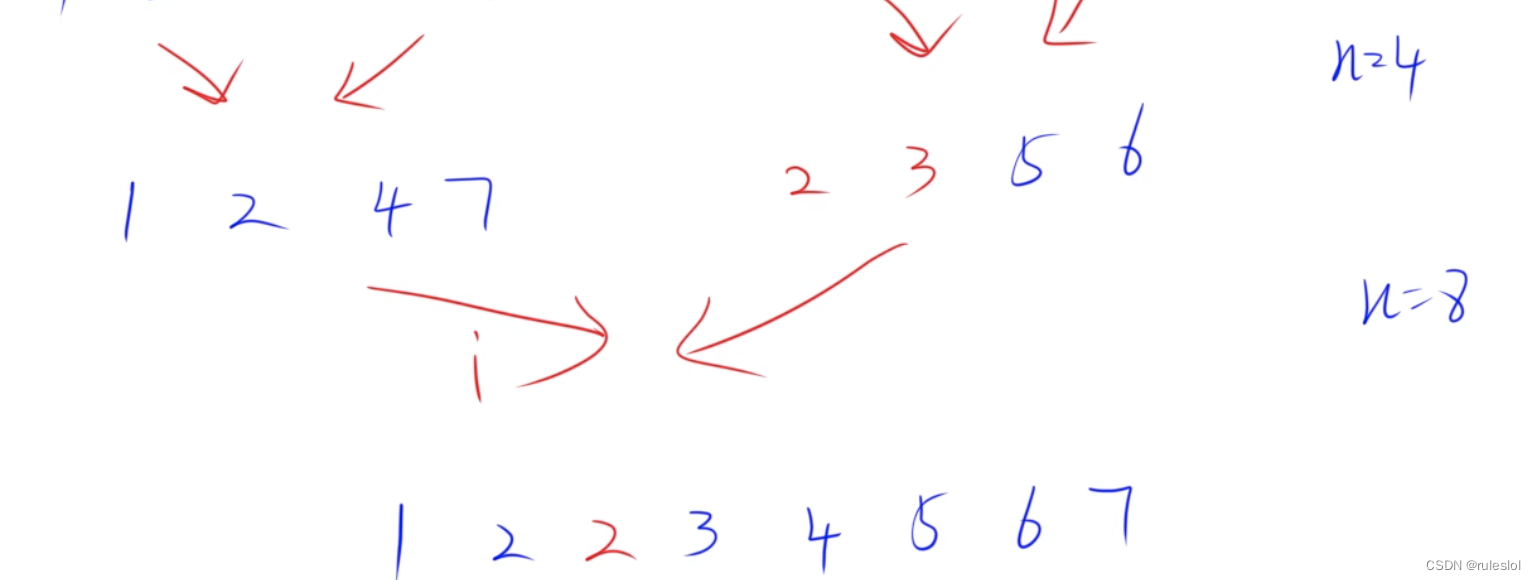
设计方法:分治法
不归并
稳定

11-1、真题
真题1:

真题2:
 真题3:
真题3:

真题4:

真题5:

真题6:

十二、排序小结
12-1、简单排序
1、直接插入排序(稳定)
2、冒泡排序(稳定)
3、简单选择排序(不稳定)
时间复杂度都是:O(n^2)
空间复杂度:O(1)
12-2、希尔排序(不稳定)
时间复杂度:O(n^1.3)
空间复杂度:O(1)
12-3、快速排序(不稳定)
分治思想
时间复杂度:O(nlog2n)——性能最好
空间时间复杂度:O(log2n)
但是,当待排序列基本有序的时候,是最坏的情况,时间复杂度退化为:O(n^2)
12-4、堆排序(不稳定)
时间复杂度:O(nlog2n)
空间时间复杂度:O(1)
12-5、归并排序(稳定)
俩俩归并,n/2向上取整
整个归并排序,需要进行log2n趟(向上取整)
空间复杂度:O(n)
时间复杂度:O(nlogn)
12-6、小结-稳定的排序
- 直接插入排序;
- 冒泡排序
- 归并排序
12-7、真题
真题1:

真题2:
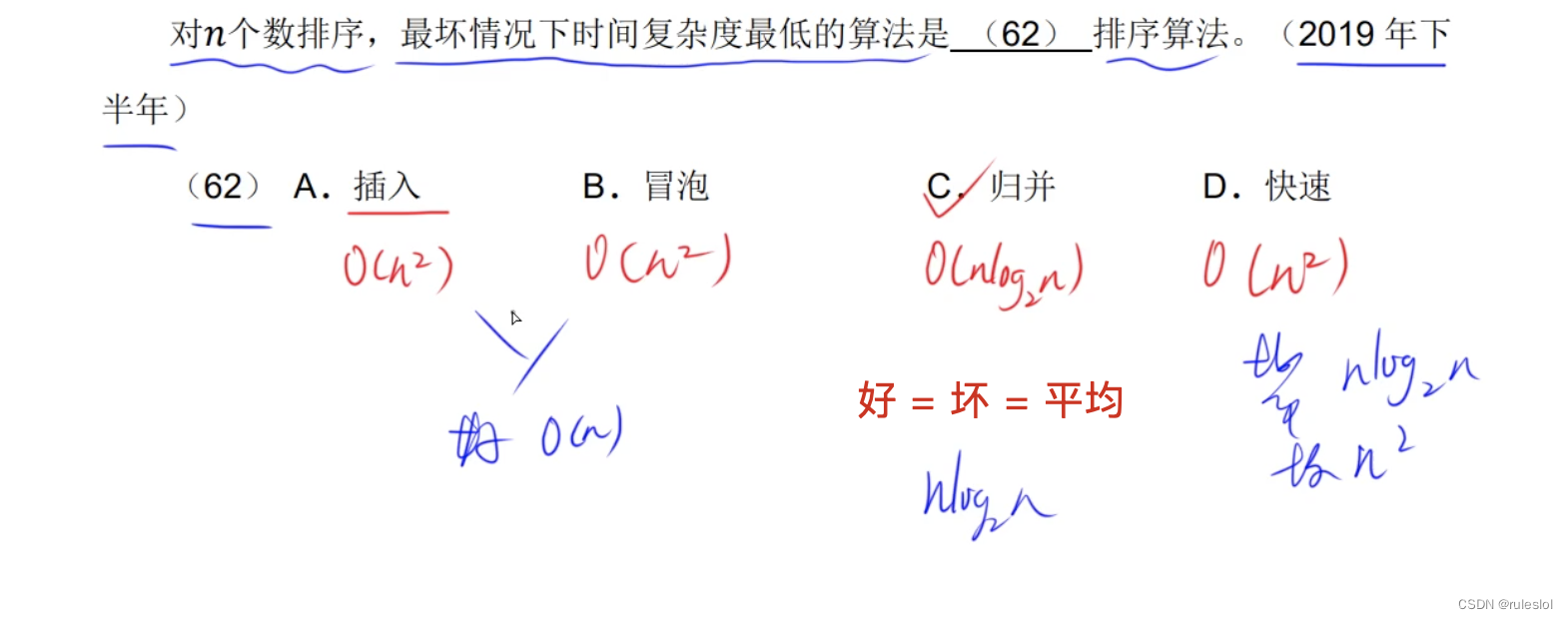
真题3:

直接插入排序:局部有序
冒泡:每一趟排序,都将最大的泡泡在最后的位置。