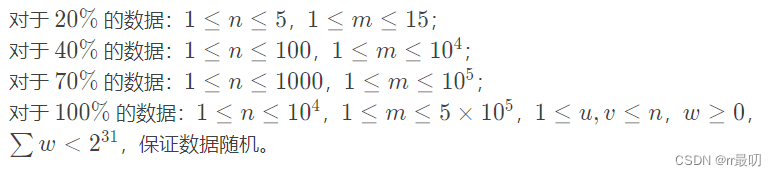解释一下什么叫邻接矩阵：

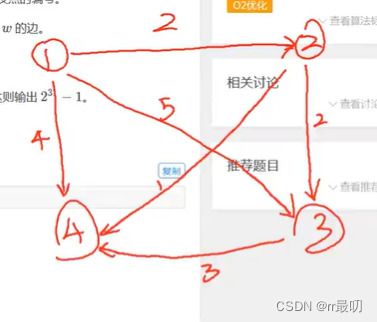
假设有以下无向图：

     1/ \2---3/ \ / \4---5---6

对应的邻接矩阵为：

    1  2  3  4  5  6
1  0  1  1  0  0  0
2  1  0  1  1  1  0
3  1  1  0  0  1  1
4  0  1  0  0  1  0
5  0  1  1  1  0  1
6  0  0  1  0  1  0
 

方法1：

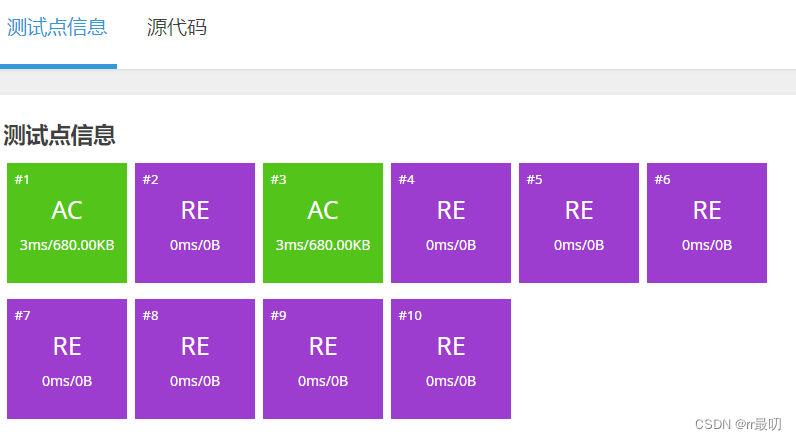
邻接矩阵加 dijkstra算法没过damnnnnn

代码如下：

#include<stdio.h>
#include<limits.h>int main() {int e[100][100], dis[100], book[100], min, n, m, s, from, to, length;int INF = INT_MAX;scanf("%d %d %d", &n, &m, &s); // 分别表示点的个数、有向边的个数、出发点的编号。// 初始化图的邻接矩阵，将所有边的权重初始化为无穷大for(int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {if (i == j) {e[i][j] = 0;}else {e[i][j] = INF;}}}// 读入图的边信息，并更新边的权重为最小值for (int i = 1; i <= m; i++) {scanf("%d %d %d", &from, &to, &length);e[from][to] = (e[from][to] > length ? length : e[from][to]);	}// 初始化 dis 数组为从源点 s 出发到各个节点的距离for (int i = 1; i <= n; i++) {dis[i] = e[s][i];}// 初始化 book 数组，标记源点 s 为已访问for (int i = 1; i <= n; i++) {book[i] = 0;}book[s] = 1;// 使用 Dijkstra 算法求解最短路径for (int i = 1; i <= n; i++) {min = INF;int u = 0;// 找到当前未访问节点中距离源点 s 最近的节点 ufor (int j = 1; j <= n; j++) {if (book[j] == 0 && dis[j] < min) {min = dis[j];u = j;}}if (u == 0) {break; // 如果 u 为 0，说明所有节点都已经访问完毕，直接跳出循环}book[u] = 1; // 标记节点 u 为已访问// 更新从源点 s 到未访问节点的距离for (int v = 1; v <= n; v++) {if (e[u][v] < INF) {if (dis[v] > dis[u] + e[u][v]) {dis[v] = dis[u] + e[u][v];}}}}// 输出结果for (int i = 1; i <= n; i++) {printf("%d ", dis[i]);}printf("\n");return 0;
}

 注意的几点：

1.

if (u == 0) {break; // 如果 u 为 0，说明所有节点都已经访问完毕，直接跳出循环}

这个一定要有，不然进入死循环，返回一个很奇怪的负整数

2.

这个代码的整体思路如下，详细的文字解释也附上

后来我改用动态内存分配： 

#include <stdio.h>
#include <stdlib.h>
#include <limits.h>int main() {int n, m, s, from, to, length;int **e, *dis, *book;int INF = INT_MAX;scanf("%d %d %d", &n, &m, &s);// 分配邻接矩阵的内存空间e = (int **)malloc((n + 1) * sizeof(int *));for (int i = 1; i <= n; i++) {e[i] = (int *)malloc((n + 1) * sizeof(int));}// 初始化邻接矩阵for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {if (i == j) {e[i][j] = 0;} else {e[i][j] = INF;}}}// 读入图的边信息并更新邻接矩阵for (int i = 1; i <= m; i++) {scanf("%d %d %d", &from, &to, &length);e[from][to] = (e[from][to] > length ? length : e[from][to]);}// 分配距离数组和标记数组的内存空间dis = (int *)malloc((n + 1) * sizeof(int));book = (int *)malloc((n + 1) * sizeof(int));// 初始化距离数组和标记数组for (int i = 1; i <= n; i++) {dis[i] = e[s][i]; // 初始化距离数组，这里是 s 号点到其余各个顶点的初始距离book[i] = 0;}book[s] = 1; // 因为 s 到 s 的距离是 0，所以把它放在标记数组里表示已访问// Dijkstra 算法主循环for (int i = 1; i <= n; i++) {int min = INF;int u = 0;for (int j = 1; j <= n; j++) {if (book[j] == 0 && dis[j] < min) {min = dis[j];u = j;}}if (u == 0) {break; // 如果 u 为 0，说明所有节点都已经访问完毕，直接跳出循环}book[u] = 1; // 标记节点 u 为已访问// 更新距离数组for (int v = 1; v <= n; v++) {if (e[u][v] < INF) {if (dis[v] > dis[u] + e[u][v]) {dis[v] = dis[u] + e[u][v];}}}}// 输出结果for (int i = 1; i <= n; i++) {printf("%d ", dis[i]);}printf("\n");// 释放动态分配的内存for (int i = 1; i <= n; i++) {free(e[i]);}free(e);free(dis);free(book);return 0;
}

 还是寄了...

再后来。。。

很明显发现这个是一个稀疏图

举个简单的例子来说明：

1 --> 2
2 --> 3, 4
3 --> 1
4 --> 5

使用邻接矩阵表示的话，会是一个5x5的矩阵，其中只有少数几个位置有非零值，其余都是零。这样就会浪费大量的空间。

而使用邻接表来表示的话，对于每个节点，只需要存储其邻居节点的列表。比如：

• 节点1的邻居节点是2；
• 节点2的邻居节点是3和4；
• 节点3的邻居节点是1；
• 节点4的邻居节点是5；
• 节点5的邻居节点为空。

这样，通过邻接表可以用更少的空间来表示图，特别是对于稀疏图来说，节省的空间更为显著。

邻接表：

 假设我们有以下图：

1 --> 2 (weight: 5)
|     |
v     v
3 <-- 4 (weight: 7)

图中有四个顶点，编号分别为1、2、3、4。边的权重分别为5和7。

现在我们来构建邻接表表示这个图：

首先，我们需要分配一个头指针数组，数组大小为顶点的个数加一：

Node** graph = (Node**)malloc((4 + 1) * sizeof(Node*));

1. 然后，我们逐条添加边到邻接链表中：

• 对于顶点1，有边连接到顶点2和顶点3，边的权重分别为5和无穷大。

• 对于顶点2，有边连接到顶点4，边的权重为无穷大。

• 对于顶点3，有边连接到顶点4，边的权重为7。

• 对于顶点4，没有出边。

因此，我们得到以下邻接表：

graph[1]: -> (2, 5) -> (3, INF) -> NULL
graph[2]: -> (4, INF) -> NULL
graph[3]: -> (4, 7) -> NULL
graph[4]: -> NULL

其中，-> 表示链表中的指针，(顶点编号, 边的权重) 表示链表节点的内容。INF代表无穷大。

#include <stdio.h>
#include <stdlib.h>
#include <limits.h>// 定义图节点的结构体
typedef struct Node {int vertex;         // 相邻顶点的编号int weight;         // 边的权重struct Node* next;  // 指向下一个相邻节点的指针
} Node;int main() {int n, m, s, from, to, length;int INF = INT_MAX;scanf("%d %d %d", &n, &m, &s); // 输入点的个数、边的个数、起始点// 分配邻接表的头指针数组，因为是二维的所以要Node**Node** graph = (Node**)malloc((n + 1) * sizeof(Node*));//因为下标是从1开始，所以要+1for (int i = 1; i <= n; i++) {graph[i] = NULL;  // 初始化每个顶点的邻接表为空}// 读入图的边信息并构建邻接表for (int i = 1; i <= m; i++) {scanf("%d %d %d", &from, &to, &length);// 创建新的节点Node* newNode = (Node*)malloc(sizeof(Node));newNode->vertex = to;newNode->weight = length;newNode->next = graph[from];  //想了一个晚上这里是怎么来的，结果发现是头插法，意思就是后插入的在前面，类似栈，就是插的新的在前面，后的往后退这样子graph[from] = newNode;}// Dijkstra 算法，这里和上面的一样int* dis = (int*)malloc((n + 1) * sizeof(int));  // 存储最短路径距离int* book = (int*)malloc((n + 1) * sizeof(int)); // 标记节点是否已经访问for (int i = 1; i <= n; i++) {dis[i] = INF;   // 初始化距离为无穷大book[i] = 0;    // 初始化标记数组为未访问}dis[s] = 0;         // 起始点到自身的距离为 0// Dijkstra 算法主循环for (int i = 1; i <= n; i++) {int min = INF;int u ;// 找到当前未访问节点中距离起点最近的节点for (int j = 1; j <= n; j++) {if (!book[j] && dis[j] < min) {min = dis[j];u = j;}}book[u] = 1; // 标记节点 u 为已访问// 更新从起点到未访问节点的距离for (Node* cur = graph[u]; cur != NULL; cur = cur->next) {int v = cur->vertex;if (!book[v] && dis[u] + cur->weight < dis[v]) {dis[v] = dis[u] + cur->weight;}}}// 输出结果for (int i = 1; i <= n; i++) {printf("%d ", dis[i]);}printf("\n");// 释放动态分配的内存for (int i = 1; i <= n; i++) {Node* cur = graph[i];while (cur != NULL) {Node* temp = cur;cur = cur->next;free(temp);}}free(graph);free(dis);free(book);return 0;
}

 最后的释放过程说明：

痛苦的快乐着。。。希望你们可以看懂