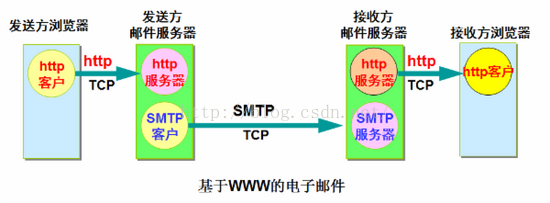
一、问题
0.1 + 0.2 === 0.3 // false
二、浮点数
“浮点数”是一种表示数字的标准,整数也可以用浮点数的格式来存储
我们也可以理解成,浮点数就是小数
在JavaScript中,现在主流的数值类型是Number,而Number采用的是IEEE754规范中64位双精度浮点数编码
这样的存储结构优点是可以归一化处理整数和小数,节省存储空间
对于一个整数,可以很轻易转化成十进制或者二进制。但是对于一个浮点数来说,因为小数点的存在,小数点的位置不是固定的。解决思路就是使用科学计数法,这样小数点位置就固定了
而计算机只能用二进制(0或1)表示,二进制转换为科学记数法的公式如下:

其中,a的值为0或者1,e为小数点移动的位置
举个例子:
27.0转化成二进制为11011.0 ,科学计数法表示为:
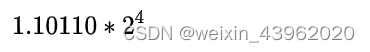
前面讲到,javaScript存储方式是双精度浮点数,其长度为8个字节,即64位比特
64位比特又可分为三个部分:
- 符号位S:第 1 位是正负数符号位(sign),0代表正数,1代表负数
- 指数位E:中间的 11 位存储指数(exponent),用来表示次方数,可以为正负数。在双精度浮点数中,指数的固定偏移量为1023
- 尾数位M:最后的 52 位是尾数(mantissa),超出的部分自动进一舍零
三、问题分析
在javascript语言中,0.1 和 0.2 都转化成二进制后再进行运算
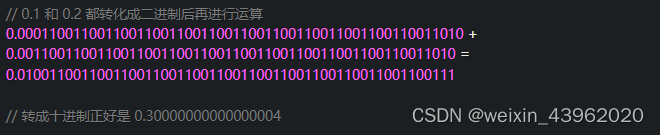
所以输出false
再来一个问题,那么为什么x=0.1得到0.1?
主要是存储二进制时小数点的偏移量最大为52位,最多可以表达的位数是2^53=9007199254740992,对应科学计数尾数是 9.007199254740992,这也是 JS 最多能表示的精度
它的长度是 16,所以可以使用 toPrecision(16) 来做精度运算,超过的精度会自动做凑整处理
![]()
但看到的 0.1 实际上并不是 0.1。用更高的精度试试:
![]()
四、结论
计算机存储双精度浮点数需要先把十进制数转换为二进制的科学记数法的形式,然后计算机以自己的规则{符号位+(指数位+指数偏移量的二进制)+小数部分}存储二进制的科学记数法
因为存储时有位数限制(64位),并且某些十进制的浮点数在转换为二进制数时会出现无限循环,会造成二进制的舍入操作(0舍1入),当再转换为十进制时就造成了计算误差