什么是平衡二叉树

AVL是一种自平衡二叉搜索树（self-balancing binary search tree）的数据结构，它的名称来源于其发明者G.M. Adelson-Velsky和E.M. Landis。AVL树通过在每次插入或删除节点时进行旋转操作，来确保树的高度始终保持在一个较小的范围内，从而保持树的平衡性。

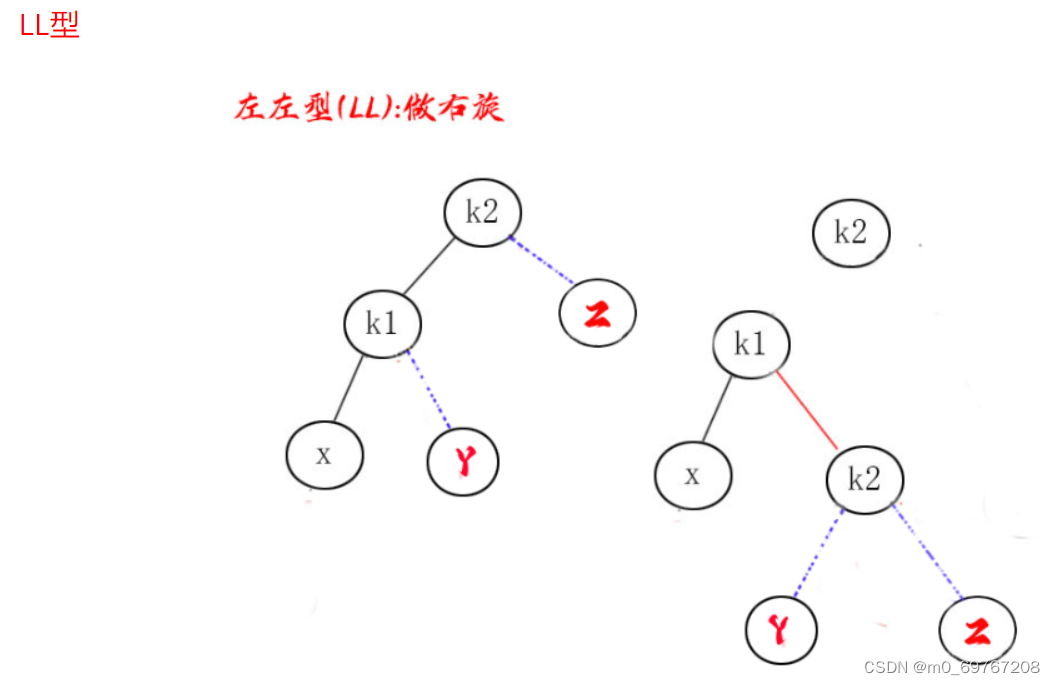
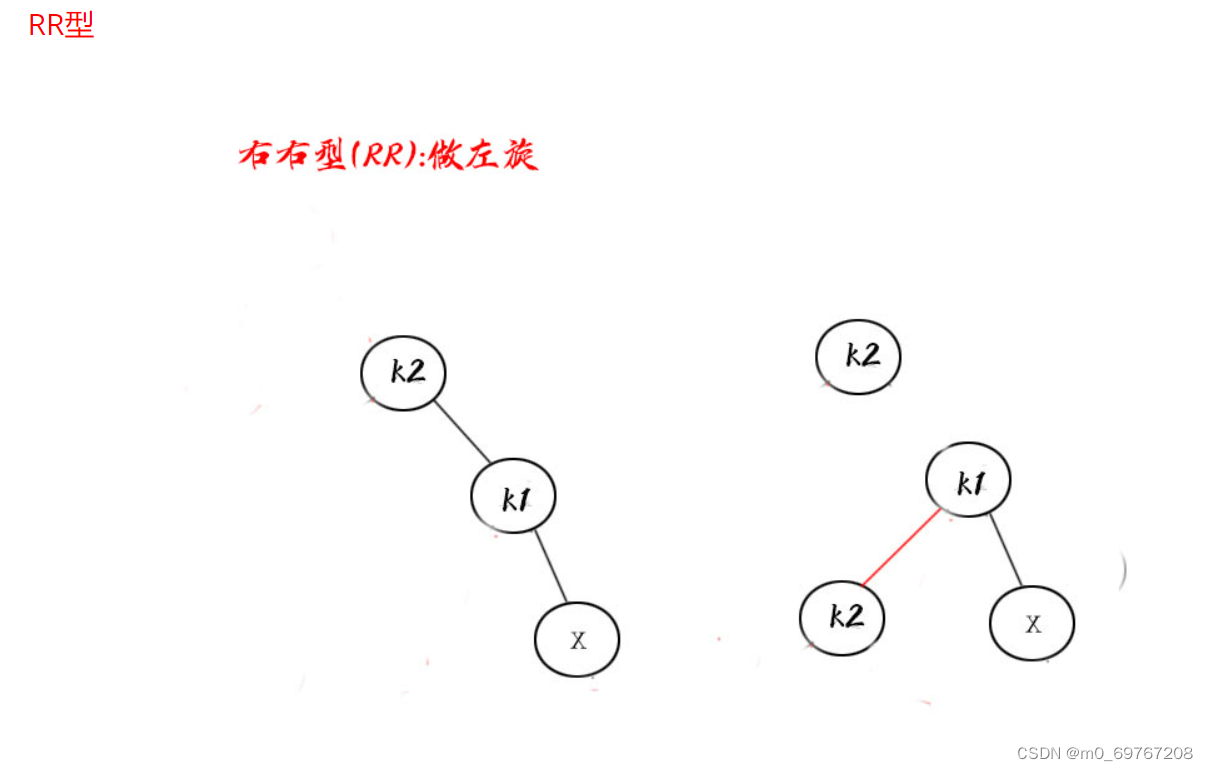
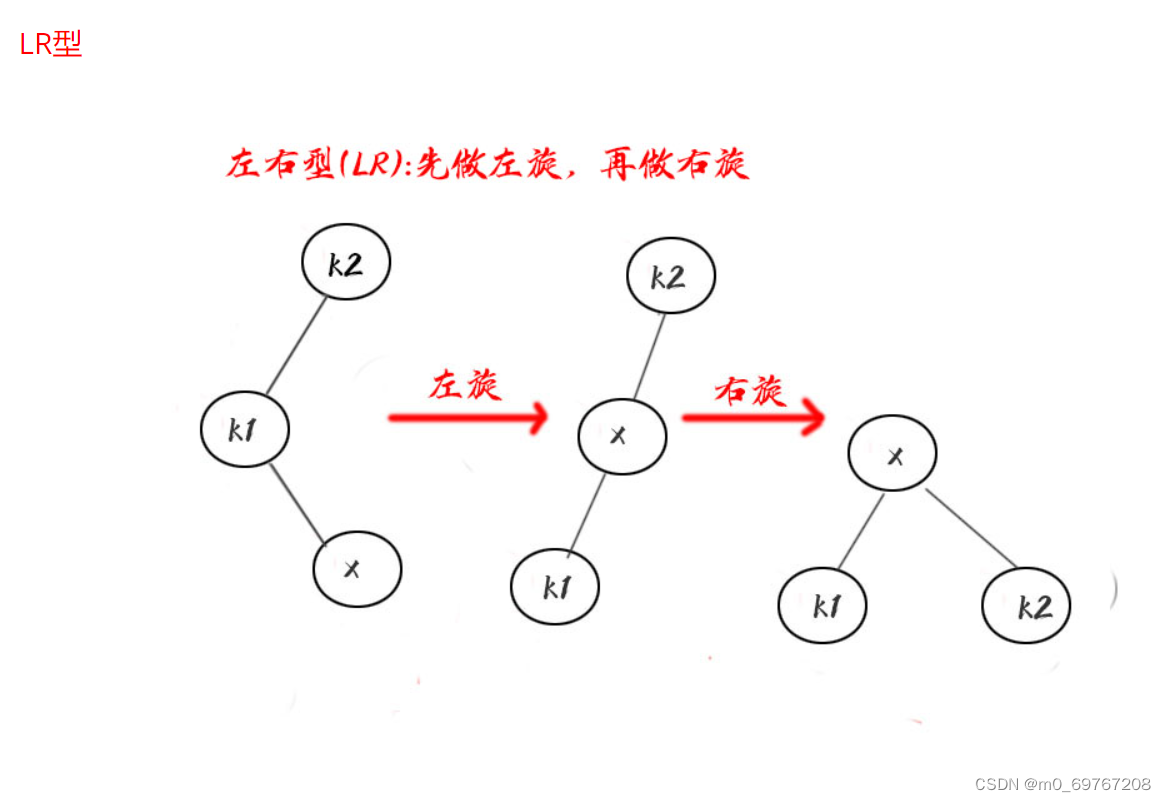
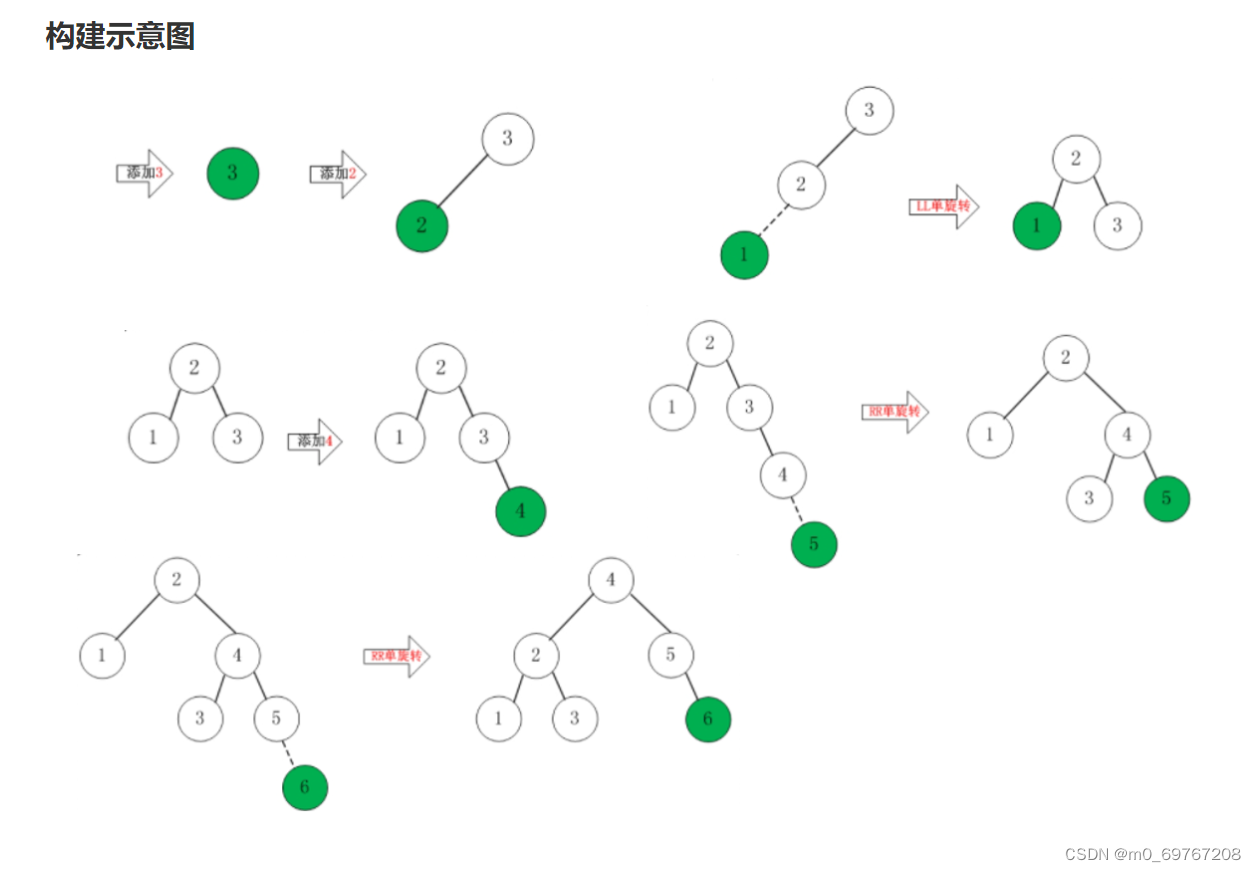
AVL树的平衡性是通过节点的高度差（即左子树高度和右子树高度之差）来衡量的。在一个平衡的AVL树中，任何节点的左子树和右子树的高度差不超过1。当插入或删除节点导致某个节点的平衡被打破时，AVL树会通过旋转操作来恢复平衡。AVL树的旋转操作分为四种类型：左旋、右旋、左右旋和右左旋。左旋和右旋用于处理节点的子树高度差为2的情况，而左右旋和右左旋用于处理节点的子树高度差为-2的情况。通过这些旋转操作，AVL树可以在插入或删除节点时保持平衡，并且可以在O(log n)的时间复杂度内进行插入、删除和查找操作。AVL树在许多应用中都有广泛的应用，特别是在需要高效的插入、删除和查找操作的场景中。它是一种重要的数据结构，被用于数据库、编译器、操作系统等领域。

旋转操作

 

 

 

 

示例代码

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <string.h>#define HEIGHT(p) ((p==NULL)?-1:(p->height))
#define MAX(a,b) ((a)>(b)?(a):(b))typedef struct 
{int key;char value[20];
}Data;typedef struct AVLTreeNode 
{Data data;int height;struct AVLTreeNode* LChild;struct AVLTreeNode* RChild;
}Node;
//创建节点
Node* create_node(Data data) 
{Node* newNode = (Node*)malloc(sizeof(Node));assert(newNode);newNode->data = data;newNode->height = 0;newNode->LChild = NULL;newNode->RChild = NULL;return newNode;
}
//层次遍历
void print_tree(Node* tree)
{if (tree == NULL)return;Node* pmove = tree;Node* queue[1024];int front = 0;int tail = 0;queue[tail++] = pmove;printf("%d:%s\n", pmove->data.key, pmove->data.value);while (front != tail){pmove = queue[front++];if (pmove->LChild != NULL){queue[tail++] = pmove->LChild;printf("%d:%s\n", pmove->LChild->data.key, pmove->LChild->data.value);}else{printf("NULL\n");}if (pmove->RChild != NULL){queue[tail++] = pmove->RChild;printf("%d:%s\n", pmove->RChild->data.key, pmove->RChild->data.value);}else {printf("NULL\n");}}
}
//LL
Node* ll_rotation(Node* k2) 
{//旋转Node* k1 = k2->LChild;k2->LChild = k1->RChild;k1->RChild = k2;//节点高度k2->height = MAX(HEIGHT(k2->LChild), HEIGHT(k2->RChild)) + 1;k1->height = MAX(HEIGHT(k1->LChild), k2->height) + 1;return k1;
}
//RR
Node* rr_rotation(Node* k1) 
{Node* k2 = k1->RChild;k1->RChild = k2->LChild;k2->LChild = k1;k1->height = MAX(HEIGHT(k1->LChild), HEIGHT(k1->RChild)) + 1;k2->height = MAX(HEIGHT(k2->LChild), k1->height) + 1;return k2;
}
//LR
Node* lr_rotation(Node* k3) 
{k3->LChild = rr_rotation(k3->LChild);return ll_rotation(k3);}
//RL
Node* rl_rotation(Node* k3) 
{k3->RChild = ll_rotation(k3->RChild);return rr_rotation(k3);
}Node* insert_avl(Node* tree, Data data) 
{if (tree == NULL)tree = create_node(data);else if (data.key < tree->data.key) {tree->LChild = insert_avl(tree->LChild, data);if (HEIGHT(tree->LChild) - HEIGHT(tree->RChild) == 2) {if (data.key < tree->LChild->data.key) {tree = ll_rotation(tree);}else {tree = lr_rotation(tree);}}}else if (data.key > tree->data.key) {tree->RChild = insert_avl(tree->RChild, data);if (HEIGHT(tree->RChild) - HEIGHT(tree->LChild) == 2) {if (data.key > tree->RChild->data.key) {tree = rr_rotation(tree);}else {tree = rl_rotation(tree);}}}else {printf("插入失败！关键字唯一!\n");}tree->height = MAX(HEIGHT(tree->LChild), HEIGHT(tree->RChild)) + 1;return tree;
}
Node* max_node(Node* tree) 
{if (tree == NULL)return NULL;while (tree->RChild != NULL) {tree = tree->RChild;}return tree;
}
Node* min_node(Node* tree)
{if (tree == NULL)return NULL;while (tree->LChild != NULL) {tree = tree->LChild;}return tree;
}
Node* erase_avl(Node* tree, int key)
{if (tree == NULL)return NULL;if (key < tree->data.key){tree->LChild = erase_avl(tree->LChild, key);if (HEIGHT(tree->RChild) - HEIGHT(tree->LChild) == 2){Node* rightNode = tree->RChild;if (rightNode != NULL && HEIGHT(rightNode->LChild) > HEIGHT(rightNode->RChild)){tree = rl_rotation(tree);}else{tree = rr_rotation(tree);}}}else if (key > tree->data.key){tree->RChild = erase_avl(tree->RChild, key);if (HEIGHT(tree->LChild) - HEIGHT(tree->RChild) == 2){Node* leftNode = tree->LChild;if (leftNode != NULL && HEIGHT(leftNode->RChild) > HEIGHT(leftNode->LChild)){tree = lr_rotation(tree);}else{tree = ll_rotation(tree);}}}else{if (tree->LChild != NULL && tree->RChild != NULL) {if (HEIGHT(tree->LChild) > HEIGHT(tree->RChild)) {Node* max = max_node(tree->LChild);tree->data = max->data;tree->LChild = erase_avl(tree->LChild, max->data.key);}else {Node* min = min_node(tree->RChild);tree->data = min->data;tree->RChild = erase_avl(tree->RChild, min->data.key);}}else {Node* temp = tree;tree = tree->LChild ? tree->LChild : tree->RChild;free(temp);}}return tree;
}void test_avl()
{Data data[10] = { 0,"小美",1,"小芳",2,"小丽",3,"小小",4,"悠悠",5,"小妹",6,"小梅",7,"小爱",8,"笑笑",9,"筱花" };Node* root = NULL;for (int i = 0; i < 10; i++) {root = insert_avl(root, data[i]);}print_tree(root);printf("----------------------\n");root=erase_avl(root, 7);print_tree(root);
}
int main() 
{test_avl();return 0;
}