介绍

这是对梁灿彬的《微分几何与广义相对论》一书的阅读记录，对微分几何这种比较复杂的数学理论没经过在学校大量练习，还不做一些笔记，是难以熟悉掌握的。这里会结合我自身的知识储备，记录下微分几何的知识递进脉络。

集合论与映射

只需要了解过高中和大学掌握的朴素集合论，就可以进入微分几何的学习，这里不做阐述。

映射相关定义

映射也是高中就涉及到的知识，但它的具体定义在高数题目中其实很少用到，感觉不太熟悉这一方面，这里列出书上给出的严格定义。

映射（map）

定义：设$X$，$Y$是非空集合，一个从$X$到$Y$的映射（map），记作$f:X\to Y$，是一个法则$f$，它给$X$中每个元素，指定$Y$中唯一的对应元素。若$y\in Y$是$x\in X$的对应元素，写作$y=f(x)$，称$y$为$x$在映射$f$下的像（image），称$x$为$y$的原像或逆像（inverse image）。$X$称为映射$f$的定义域（domain），$X$的所有元素在映射$f$下的像的集合，记作$f[X]$，称为映射$f:X\to Y$的值域（range）。

以下给出一些常用记法和说明：

• 映射的相等：当且仅当$f(x)=f^{\prime }(x),\forall x\in X$，映射$f:X\to Y$和映射$f^{\prime }:X\to Y$相等。
• $y=f(x)$的另一种记法为：$f:x\mapsto y$
• 在映射$f$下部分像的集合，可以记为 f [ A ] = { y ∈ Y ∣ ∃ x ∈ A , y = f ( x ) } ⊂ Y f[A]=\{y\in Y| \exists x\in A, y=f(x)\}\subset Y f[A]={y∈Y∣∃x∈A,y=f(x)}⊂Y

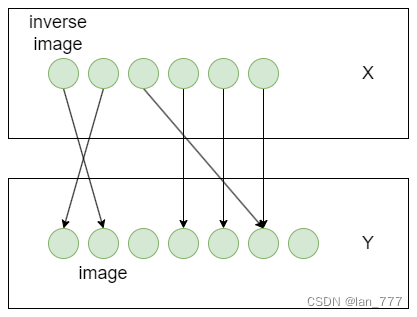
上图是映射的简单示意图，可以加深印象，认识到$X$中每个元素都会映射到$Y$，形象化的说就是$X$中每个元素都会伸出一个箭头到$Y$中某元素上；但$Y$中的元素则没有什么严格约束，可以多个箭头连到一个元素上，也可以有没有箭头连的“孤独的元素”。

映射的一种分类：一一的和到上的

定义： 映射$f:X\to Y$是一一的（one-to-one)，当且仅当任意一个$y\in Y$，有不多于一个原像；$f:X\to Y$是到上的（onto），当且仅当任意一个$y\in Y$都有原像。

这里是梁书中的叫法，其他书中有用单射（injection）和满射（surjection）的，它们对应上述定义的一一和到上。

既是一一的又是到上的映射被称为一一到上的，其他书中可能称为双射（bijection）或一一映射，这种一一映射会强于之前定义的一一的。为避免歧义，一一的仅用于指单射。

单射和满射的概念很简单，但不经常锻炼又容易混淆，这里从名字上来速记。单射和满射都是针对$Y$的约束，单射中的单对应至多1个，意思是$Y$中元素被至多一个箭头指向；满射中的满对应所有，即所有$Y$中的元素都有箭头指向它。

拓扑空间

背景介绍

如果映射$f:X\to Y$中，$X=R$且$Y=R$，那么$f$就表示定义域为$R$的一元函数。这个映射不仅可以定义一一到上的要求，还可以定义连续性，可微性等诸多有用的属性。高等数学中对连续性的定义依赖于距离这个概念：
$$\forall \epsilon >0,\exists \delta >0,when|x^{\prime }-x|<\delta ,|f(x^{\prime })-f(x)|<\epsilon$$
这里，两个不等式实质上都是暗示数轴上的距离大小关系相互依赖。只有距离能定义，这种连续性才可以定义，这肯定无法推广到任意集合上，因为有些集合无法定义出距离。

然而，细想一下，似乎连续性有另一种不依赖于距离的定义方式，即：使用开区间定义，描述如下：

设$X=Y=R$，当且仅当$Y$中任一开区间的“逆像”都是$X$的开区间之并（或空集），$f:X\to Y$是连续的。

不给出证明，只考虑一下这个定义能不能去排除间断点即可。

• 对于可去间断点，在那个间断点附近取$Y$的一个很小的开区间，逆像将只有一个元素，一个元素显然不可能是开区间，也不可能表示为开区间之并，因此背离定义，是不连续的。
• 对于跳跃间断点，在跳跃点总能取到一个开区间，让原像包含一端闭区间，只要有一端是闭区间，就不可能表示为开区间之并。
• 对于无穷间断点，补充定义的话，只要包含定义的点，那么原像就包含闭区间。
• 对于震荡间断点，同样在无定义点补充定义的话，那么原像也要包含一个只有一个元素的区间，其他开区间将无限趋近于这个点。

开子集

上述开区间之并的概念很重要，不仅可以用于定义连续性，还可以推广到任意集合。$R$的可表示为开区间之并的子集我们称为开子集。我们将开子集的概念进行推广。

开子集的选择

在$R$上有天然的开子集定义，使用开区间来定义即可。但对于任意集合，可能都不存在数轴的概念，无法定义开区间，我们则需要指定一种开子集的定义方式。同一集合可以定义多种开子集，我们先对定义方式做出约束，即开子集需要满足的基本性质：

• $X$集本身和空集$\varnothing$为开子集
• 有限个开子集之交为开子集
• 任意个开子集之并为开子集

可见，只定义$\varnothing$和$X$为开子集，其他子集都不是开子集，这就是一种开子集的定义方式；指定$X$的所有子集都是开子集也是一种定义方式。只不过这两种定义方式都是比较平凡的，除了满足性质外，没有对集合$X$附加什么约束。

拓扑

当我们为一个集合$X$定义了一种开子集，就是为$X$附加了一种额外结构，即拓扑结构。

定义了拓扑结构的集合$X$的全体开子集的集合，被称为$X$的一个拓扑。书上将一个拓扑用花体符号来写，笔记里就简单记录为$T$。

更符号化的写法是：非空集合$X$的一个拓扑（topology）$T$是$X$的若干子集的集合，满足：

• $X\in T,\varnothing \in T$
• 若$O_i\in T$，$i=1,2,\cdots ,n$，则$\underset{i=1}{\bigcap ^n}{O}_i\in T$
• 若$O_{\alpha }\in T,\forall \alpha$，则$\bigcap _{\alpha }{O}_{\alpha }\in T$

拓扑空间

定义了拓扑$T$的集合$X$称为拓扑空间，记为$(X,T)$，明确了拓扑时，也可只记为$X$。

常见拓扑

• 离散拓扑：指定$X$中所有子集为开子集所定义的拓扑。
• 凝聚拓扑：只指定$X$和$\varnothing$为开子集所定义的拓扑。
• $R$的通常拓扑：指定$\varnothing$或$R$中能表示为开区间之并的子集为开子集所定义的拓扑。
• $R^n$的通常拓扑：指定$\varnothing$或$R^n$中能表示为开球之并的子集为开子集所定义的拓扑。其中开球是集合 B ( x 0 , r ) = { x ∈ R n ∣ ∣ x − x 0 ∣ < r } B(x_0,r)=\{x\in R^n|\ |x-x_0|<r\} B(x0​,r)={x∈Rn∣ ∣x−x0​∣<r}，可以发现$n=1$时，开球就是开区间。
• 乘积拓扑：设两个拓扑空间$(X_1,T_1)$和$(X_2,T_2)$，$X=X_1\times X_2$（笛卡尔积），定义$X$的拓扑为： T = { O ∈ X ∣ O T=\{O\in X | O T={O∈X∣O可表示为形如$O_1\times O_2$的子集之并，$O_1\in T_1,O_2\in T_2\}$，乘积拓扑可以推广到$n$个拓扑的乘积，$R^n$就是$R$的乘积拓扑。

拓扑子空间

对于拓扑空间$(X,T)$来说，$X$有一个非空子集$A$，$A$也可指定一个拓扑$T_S$，使得$A$也成为拓扑空间。

如果$A\in T$，即$A$是$X$在拓扑$T$下的开子集，那么$T_S$很好定义，只要定义 T S = { V ⊂ A ∣ V ∈ T } T_S=\{V\subset A | V\in T\} TS​={V⊂A∣V∈T}，即$A$的所有子集中，属于$T$的那些，都定义为$A$的开子集即可。然而如果$A$不是$X$的开子集，那么按照上述$T_S$的定义，$A\notin T_S$，这违背了拓扑空间的定义。

一个更巧妙的$T_S$的定义是：
T S = { V ⊂ A ∣ ∃ O ∈ T , V = A ∩ O } T_S=\{V\subset A | \exist O\in T, V=A\cap O\} TS​={V⊂A∣∃O∈T,V=A∩O}
这样即使$A$不是$X$的开子集，$T_S$也满足拓扑的要求。$T_S$叫做$A$的、由$T$导出的诱导拓扑，$(A,T_S)$称为$(X,T)$的拓扑子空间。

诱导拓扑是一个比较抽象的概念，书上举了一个很好的例子加深理解，$R^2$上的通常拓扑是一个个开圆盘的并，在$R^2$中随便找一个圆周，它肯定不是开子集，但它上面也可以定义拓扑，就是用开圆盘和圆周相交，交的结果作为圆周的开子集。

这里我加入一些个人的理解，按开子集是开区间的抽象，是对集合的几何性质的一种描述，我们取$R^2$上通常拓扑的情况下，很显然一个个开球或开球之并是开区间之并，但二维空间中的圆周它本身也是连续的，按理说在上面定义一个和$R^2$中开区间意义接近的开区间也不难，但它不符合$R^2$上的开区间定义，所以诱导拓扑就是弱化了拓扑的定义，从而方便在这样的几何形状上复用$R^2$的拓扑结构，而无需再定义一个额外的拓扑。

同胚

在拓扑空间中重新定义连续：设$(X,T)$和$(Y,T_S)$为拓扑空间，映射$f:X\to Y$是连续的，当且仅当$f^{-1}[O]\in T,\forall O\in T_S$。

单点连续定义：设$(X,T)$和$(Y,T_S)$为拓扑空间，映射$f:X\to Y$在$x\in X$处连续，当且仅当对于$Y$中任意包含$f(x)$的开子集$G^{\prime }$，总存在$X$的一个开子集$G$，使得$x\in G$且$f[G]\subset G^{\prime }$。（原书中符号表达是这样的：$\forall$满足$f(x)\in G^{\prime }$的$G^{\prime }\in T_S$，$\exists G\in T$使得$x\in G$且 $f[G]\subset G^{\prime }$）

同胚：$(X,T_X)$和$(Y,T_Y)$称为互相同胚的（homeomorphic to each other），当且仅当存在一个映射$f:X\to Y$，满足：

• $f$是一一到上的；
• $f$和$f^{-1}$都连续。

这样，$f$称为$(X,T_X)$到$(Y,T_Y)$的同胚映射，简称同胚。

为什么同胚定义要求映射一一到上的，还要求$f$和$f^{-1}$都连续？按理说一一到上且$f$连续，那么$f^{-1}$就一定连续。实际上$R$在通常拓扑下确实是这样，但这里是任意的拓扑。只需要将$T_X$取为凝聚拓扑，$T_Y$取为离散拓扑，那么$f$连续，$f^{-1}$将大概率不连续，即使映射是一一到上的。

可微性可否推广？连续性可微性有一个通用的记法$C^n$，即$n$阶导函数存在且连续。$C^0$就对应连续性，$C^{\infty }$对应光滑。$C^0$可以推广到拓扑空间的映射，但对于更高的要求则不能。事实上，拓扑空间之间的映射最高要求就是同胚，同胚在$X$和$Y$中元素之间建立了一一对应关系，且在开子集之间也建立了一一对应关系。一切由拓扑决定的性质会全息的被$f$携带到$Y$中，互相同胚的拓扑空间就是字面意义上像得不能再像了。

其他重要定义

这些定义其实在多元函数微积分中都存在，比如边界，内部，连通性等都能在$R^2$上的二元函数上找到对应的概念，事实上这些概念可以视为在拓扑上的延伸。

• 邻域：集合$N\subset X$称为$x\in X$的邻域，当且仅当$\exists O\in T$，使得$x\in O\subset N$，自身是开集的邻域叫开邻域。简而言之，就是一个集合能视为邻域，它就必须包含一个开子集，且$x$属于这个开子集。
• 闭集：$C\subset X$叫做闭集（closed set），当且仅当$-C\in T$。形象说，就是$C$的补集一定是开子集。闭集与开集完全对应，因此也满足3条性质，即“任意交、有限并、$X$和$\varnothing$是闭集”
• 既开又闭：显然$X$和$\varnothing$既是开集有是闭集，任何拓扑空间都有这两个既开又闭的子集。
• 连通的：只存在$X$和$\varnothing$两个既开又闭的子集的拓扑空间是连通的。不连通的例子也好想，就$R$上的两个不相交的开区间$A$和$B$，视为一个集合，由R的通常拓扑在这两个线段上诱导出的拓扑，就有两个额外的既开又闭的子集$A$和$B$。恰好这两个区域确实不连通。
• 闭包：$A$的闭包$\bar{A}$是所有包含$A$的闭集的交集。
• 内部：$A$的内部$i(A)$是所有$A$包含的开集的并集。
• 边界：$A$的边界是$\stackrel{\bullet }{A}=\bar{A}-i(A)$

开覆盖

定义：$X$的开子集的集合 { O α } \{O_\alpha\} {Oα​}叫做$A\subset X$的一个开覆盖（open cover），当且仅当$A\subset \bigcup _{\alpha }{O}_{\alpha }$。也可称 { O α } \{O_\alpha\} {Oα​}覆盖$A$。

紧致性

有限开覆盖

设 { O α } \{O_\alpha\} {Oα​}是$A\subset X$的开覆盖，如果 { O α } \{O_\alpha\} {Oα​}的有限元素的子集也覆盖$A$，称 { O α } \{O_\alpha\} {Oα​}有有限开覆盖。

紧致性

$A$的任一开覆盖都有有限开覆盖，则称$A$为紧致的。

紧致性稍微难以从直观的角度理解，选用$R$的通常拓扑举例，如果$A$是单点集（只包含一个元素），那他肯定是紧致的，任一开覆盖都必定有一个元素，这个元素包含$A$中的唯一点。

但$A$只要包含开区间，哪怕是单边开区间，$A$就不会是紧致的。比如$A=(0,1]$，可以选择一个开覆盖：$\{(1/n,2)|n\in N\}$，这一段段开子集（开区间）一段逐渐逼近$0$，无限并则肯定可以覆盖$A$，但没有任何一个有限的并可以覆盖$A$。

$R$的紧致性

对于$R$，有几个紧致性的结论，$R$本身不是紧致的；$R$的任意闭区间都紧致，$R$的任一开区间或半开区间都非紧致。

$R$的紧致性和闭集有密切联系，但不等价，具体区别可以归结为一个定理：

若$(X,T)$为$T_2$空间，$A\subset X$为紧致的，则$A$为闭集。

其中，$T_2$空间又叫做豪斯多夫空间，它指的是满足以下性质的拓扑空间：$\forall x,y\in X，x\ne y,\exists O_1,O_2\in T$，使得$x\in O_1,y\in O_2$，且$O_1\cap O_2=\varnothing$。

常见的拓扑空间都是$T_2$空间，但绝非全部。

习题

1. 试证$A-B=A\cap (X-B),\forall A,B\subset X$.

只要列举出差集的定义即可看出等式两边含义相同。
A − B = { x ∣ x ∈ A , x ∉ B } A-B=\{x|x\in A, x\notin B\} A−B={x∣x∈A,x∈/B}
X − B = { x ∣ x ∈ X , x ∉ B } X-B=\{x|x\in X, x\notin B\} X−B={x∣x∈X,x∈/B}
A ∩ ( X − B ) = { x ∣ x ∈ A , x ∈ ( X − B ) } = { x ∣ x ∈ A , x ∉ B } A\cap(X-B)=\{x | x\in A, x\in (X-B)\}=\{x | x\in A, x\notin B\} A∩(X−B)={x∣x∈A,x∈(X−B)}={x∣x∈A,x∈/B}

2. 试证$X-(B-A)=(X-B)\cup A,\forall A,B\subset X$.

根据德摩根律，$X-(B-A)=X-(B\cap (X-A))=(X-B)\cup (X-(X-A))$
其中用差集定义列举即可得知$X-(X-A)=A$

3. 判断映射$f:R\to R$是否是一一的（单射）、到上的（满射）。

$f(x)=x^3$，双射
$f(x)=x^2$，非单非满
$f(x)=e^x$，单射
$f(x)=\cos x$，非单非满
$f(x)=5$，非单非满

4. 判断下面说法正确与否

• 正切函数是由$R$到$R$的映射。否，定义域并非$R$
• 对数函数是由$R$到$R$的映射。否，定义域并非$R$
• $(a,b]\subset R$用通常拓扑衡量是开集。否，无法表示为开区间之并
• $[a,b]\subset R$用通常拓扑衡量是闭集。是，它的补集可以表示为无限个开区间之并。

5. 举出一个反例证明命题“$(R,T_u)$的无限个开子集之交为开子集”是假命题。

$(R,T_u)$指的是$R$上的通常拓扑，开子集定义为能表示为开区间之并的集合。
构造一系列开子集，$(-\frac{1}{1},\frac{1}{1}),(-\frac{1}{2},\frac{1}{2}),\cdots ,(-\frac{1}{n},\frac{1}{n})$，当$n$是无穷时，这无限个开子集之交是一个闭集$[0]$。

6. 证明诱导拓扑定义满足拓扑的基本定义。

拓扑的基本定义有三个条件，逐个检验即可：

1. 证明$A$和$\varnothing$是开子集。
   $A$一定是开子集，根据诱导拓扑的定义 T S = { V ⊂ A ∣ ∃ O ∈ T , V = A ∩ O } T_S=\{V\subset A | \exist O\in T, V=A\cap O\} TS​={V⊂A∣∃O∈T,V=A∩O}
   $V$取$A$时，肯定存在$O=X$（这是由拓扑$(X,T)$基本性质决定的），使得$A=A\cap X$
   $\varnothing$同理
2. 证明有限交。
   即证明$T_S$中有限个元素之交仍然是$T_S$的元素。
   假设$V_1,V_2,\cdots ,V_n\in T_S$，必然$\exists O_1,O_2,\cdots ,O_n\in T$，使得$V_1=A\cap O_1,V_2=A\cap O_2,\cdots ,V_n=A\cap O_n$，故$V_1\cap V_2\cap \cdots \cap V_n=A\cap (O_1\cap O_2\cap \cdots \cap O_n)$，故对于有限交$V=V_1\cap V_2\cap \cdots \cap V_n\subset A$，总存在$O=O_1\cap O_2\cap \cdots \cap O_n\in T$，使得$V=A\cap O$
3. 证明无限并。
   假设有无限个$V_{\alpha }=A\cap O_{\alpha }\subset A$，对于$V=\bigcup _{\alpha }{V}_a=\bigcup _{\alpha }(A\cap O_{\alpha })=A\cap \bigcup _{\alpha }{O}_{\alpha }=A\cap O$

7. 举例证明$(R^3,T_u)$存在不开不闭的子集。

$R$上通常拓扑很容易找到一个不开不闭的子集，比如$[1,3)$，一边开一边闭。
$R^3$是$R$的乘积拓扑，而$[1,3)$的笛卡尔积，形成一个半开半闭的立方体$[1,3{)}^3$，这就是一个不开不闭的子集。因为显然点$(1,1,1)\in R^3$不能由开球之并取到。

8. 常值映射$f:(X,T_X)\to (Y,T_Y)$是否连续？说明原因。

设$y_0\in Y$，且$f(x)=y_0,\forall x\in X$，连续就意味着，对于任意包含$y_0$的开子集，其原像也是开子集。由映射关系可知，对任意包含$y_0$的集合，其原像都是$X\in T_X$，故映射连续。

9. 设$T_D$是$X$上的离散拓扑，$T_C$是$Y$上的凝聚拓扑，找出从$(X,T_D)$到$(Y,T_C)$的所有连续映射，找出从$(Y,T_C)$到$(X,T_D)$的所有连续映射。

首先找从$(X,T_D)$到$(Y,T_C)$的连续映射，连续意味着，任何$T_C$中的开子集，其逆像是$T_D$中的开子集。由于$T_C$中的开子集只有$Y$和$\varnothing$，$\varnothing$的逆像肯定仍然是$\varnothing$，因此只要要求$f^{-1}[Y]\in T_D$即可。根据映射的基本定义，$f^{-1}[Y]=X\in T_D$，因此所有映射都是连续的。
然后找从$(Y,T_C)$到$(X,T_D)$的连续映射，即要求所有$X$的子集，逆像都属于 { Y , ∅ } \{Y,\varnothing\} {Y,∅}，那么只能是常值映射满足此要求。因为如果有两个不同的像，就$X$就有两个不同的子集，都要求$Y$是子集的逆像，但根据映射的定义，这是不可能的。

10. 证明拓扑空间点连续的定义和映射连续的定义的等价性。

等价性意味着可以互相推导出，设映射为$f:(X,T_X)\to (Y,T_Y)$。

1. 逐点连续$\to$映射连续
   $\forall B\in T_Y$，总可以分为三类，$\varnothing$，与值域有交集，与值域无交集。
   其中，如果$B$是$\varnothing$或与值域无交集，那么$f^{-1}[B]=\varnothing \in T_X$;
   如果$B$与值域有交集，则可以取到像$y\in B$，其逆像$x\in X$，由于逐点连续，那么$x$处也连续，那么必然存在$x\in A\in T_X$，使得$f[A]=B$；
   即，对任意$B$，逆像都是属于$T_X$，所证成立。
2. 映射连续$\to$ 逐点连续
   思路类似，同样挑出与值域有交集的$B\in T_Y$，其逆像$A$必然属于$T_X$；
   对任意一点$x\in A\in T_X$，找到其像$y$和包含$y$的$B$，则必然存在$A\in T_X$，使得$x\in A$，且$f[A]=B$，故$x$点连续。

11. 试证任意开区间$(a,b)\subset R$与$R$同胚。

同胚就意味着存在一个逆映射和本身都连续的双射，$f:(a,b)\to R$
很容易构造出这样的一个双射：
$$f(x)=\tan (\frac{\pi }{(b-a)}(x-\frac{a+b}{2})),x\in (a,b)$$

12. 设$X_1\subset R,X_2\subset R$，其中$X_1=(1,2)\cup (2,3)$，$X_2=(1,2)\cup [2,3)$，设$T_1$和$T_2$分别是$(R,T_u)$在$X_1$和$X_2$上的诱导拓扑，拓扑空间$(X_1,T_1)$和$(X_2,T_2)$是否连通？

连通的定义是，除了$X$和$\varnothing$外，没有即开又闭的子集。
$(X_1,T_1)$显然不连通，集合$(1,2)\in T_1$就是一个即开又闭的子集；
$(X_2,T_2)$是连通的

13. 任意集合$X$配以离散拓扑，所得的拓扑空间是否连通？

离散拓扑中，所有子集都是开子集，那么所有子集（补集）也都是闭子集，所有子集都既开又闭，必然不连通。

14. 设$A\subset B$，试证：（a）$\bar{A}\subset \bar{B}$，提示$A\subset B$说明$\bar{B}$是含$A$的闭集；（b）$i(A)\subset i(B)$

先回顾一下概念：$A$的闭包$\bar{A}$是所有包含$A$的闭集的交集；$A$的内部$i(A)$是所有$A$包含的开集的并集。
(a). 根据提示可知，$\bar{B}$是包含$A$的闭集，又由于$\bar{A}$是所有包含$A$的闭集的交集，所有$\bar{A}=\bigcap _{\alpha }{C}_{\alpha }$，其中，某个$C_{\alpha }=\bar{B}$，因此，$\bar{A}\subset \bar{B}$。
(b). 和上述思路一致，$A$包含的所有开集也必然被$B$包含。

15. 试证明$x\in \bar{A}\leftrightarrow x$ 的任一邻域与$A$的交集非空。

回顾一下邻域的概念，邻域是一个集合，它能被视为邻域需要存在一个开子集被它包含，且此开子集有元素$x$。

1. 从左推右$⟹$
   反证法，设开子集$O$是$x$的邻域，且$O\cap A=\varnothing$，故$A\subset X-O$，由上一题可知，$\bar{A}\subset X-O$，因为$X-O$本身就是闭集。故$x\in X-O$，矛盾。
2. 从右推左$⟸$
   反证法，假设$x\notin \bar{A}$，且$\forall O$作为$x$的开邻域，$O\cap A\ne \varnothing$。总存在闭集$B$，使得$A\subset B$且$x\notin B$，故$x\in X-B$，那么$(X-B)\cap A=\varnothing$且$(X-B)$是开邻域，与前设矛盾。

16. 试证明$R$不是紧致的。

回顾紧致的定义，任一开覆盖都有有限开覆盖，则紧致。
很明显$R$不是紧致的，可以找到一系列开子集$(-n,-n+2),(-n+1,-n+3)\cdots (-2,0),(1,3),\cdots ,(n,n+2)$，$n$为无穷大。这一系列开子集可以覆盖$R$，但有限的子集不能覆盖$R$，所以不是紧致的。