趣学贝叶斯定理：贝叶斯定理的先验概率、似然和后验概率(1)-编程知识

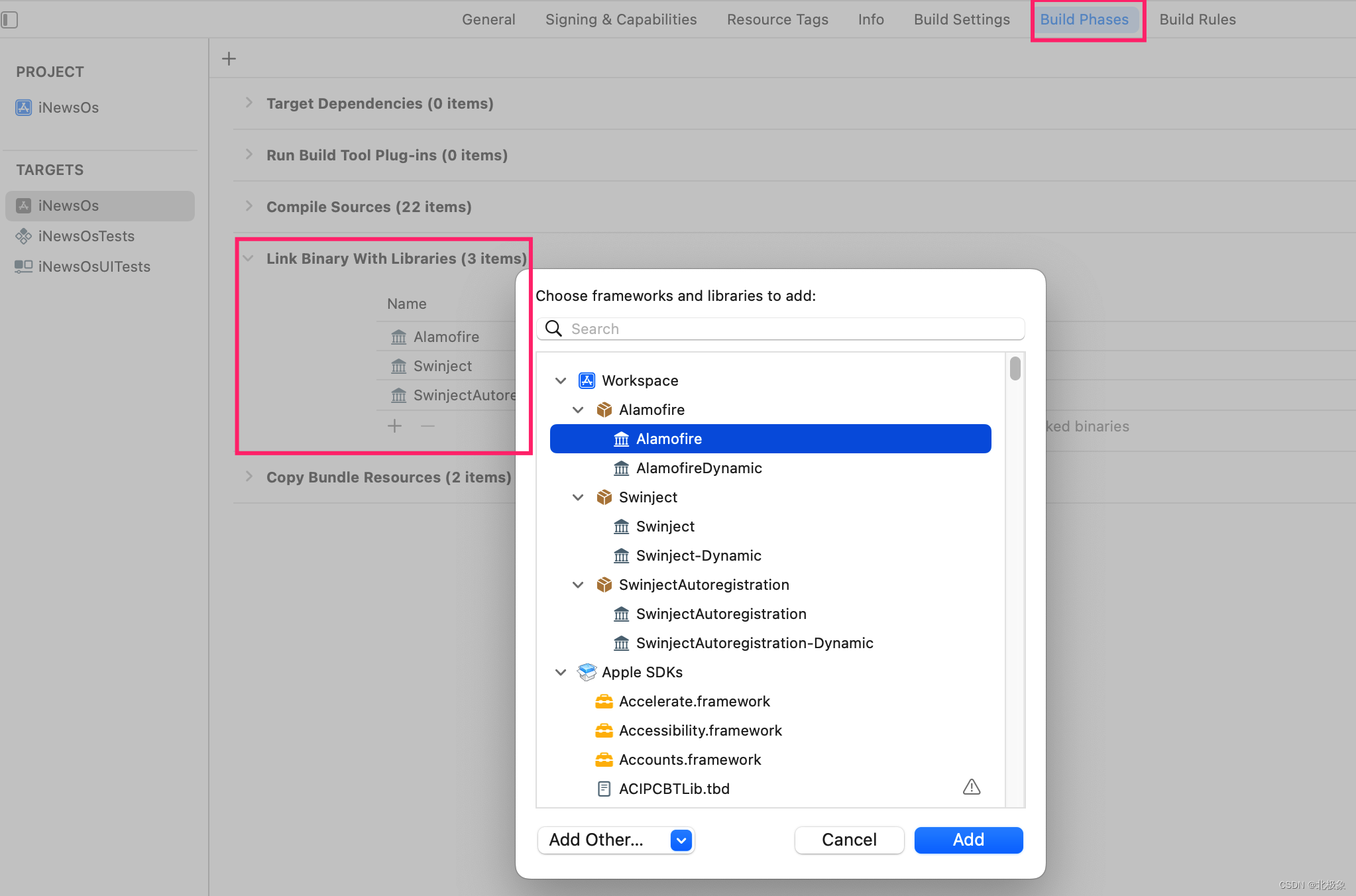
在第7章中，我们讨论了如何利用空间推理去推导贝叶斯定理。现在研究如何将贝叶斯定理当作一种概率工具，对不确定性进行逻辑推理。本章将利用贝叶斯定理来计算和量化在给定数据的情况下，信念有多大的可能性为真。为此，需要使用该定理的三要素——后验概率、似然和先验概率。这3个要素将在这场贝叶斯统计和概率探险之旅中频繁出现。

1. 贝叶斯定理三要素

我们想量化的是：在所观察到的数据下，自己对信念的坚信程度。在贝叶斯公式中，这个要素的术语是后验概率（posterior probability，简称为“后验”），也就是将通过贝叶斯定理所求出的解。
似然（likelihood）表示在给定信念的情况下，观察到某一数据的概率，也就是P(数据|信念)。
P(信念): 先验概率（priorprobability，简称为“先验”），它表示我们在看到数据之前的信念强度。似然和先验结合在一起就会形成后验。通常情况下，我们需要使用数据的概率P(数据)对后验归一化，从而使其值介于0和1之间。然而在实践中并不总是需要P(数据)，所以这个值没有特殊的名字。

2. 调查犯罪现场

假设，一天你下班回家后，发现家里的窗户玻璃碎了，前门开着，你的笔记本计算机也不见了。你的第一反应可能是：“家里被盗了！”但你是如何得出这个结论的？更重要的是，你如何量化这个信念呢？你的第一反应是家里被盗了，所以这里H=被盗。我们需要一个概率来描述家里被盗的可能性有多大，所以根据现有的数据，想要求解的后验是：P(被盗 | 窗户玻璃碎了, 前门开着, 笔记本计算机不见了)

2.1 求解似然

如果家里真的被盗了，同样的数据会被观察到的概率。换句话说，也就是数据与假设的吻合程度：P(窗户玻璃碎了, 前门开着, 笔记本计算机不见了 | 被盗)

我们可以去当地警察局询问盗窃案件犯罪现场的统计数据，或者浏览最近关于盗窃案的新闻报道。这样就可以得到更准确的似然估计：如果被盗，你看到这些数据的概率。

贝叶斯定理的不可思议之处在于，我们既可以用它来衡量信念，也可以用它来处理具有精确概率的大数据集。即使认为似然估计不是一个好的估值，你也可以随时返回去重新计算，看看在不同的假设下这个值是如何变化的。

贝叶斯统计让人们以一种可度量的方式产生不同的信念。因为是以量化的方式处理信念的，所以你可以重做本章所做的一切计算，看看不同的概率是否会对最终的结果产生实质性影响。

2.2 计算先验概率

先验概率非常重要，因为它允许我们使用背景信息对似然进行调整。假设前面描述的场景发生在一个荒岛上，而你是岛上唯一的居民，那么你家几乎不可能被盗（至少是被人类）。换一个场景，如果你家位于犯罪率很高的街区，那么盗窃事件就可能会经常发生。为简单起见，我们将被盗的先验概率设定为：1/10000
如果有不同的或额外的数据，随时可以调整这个概率。

2.3 归一化数据

P(D)：所观察到的这些数据发生的概率.
归一化的过程通常涉及到将先验概率与似然函数的乘积除以所有可能结果的概率之和（或积分），以确保后验概率的总和为1。

随着数据发生概率的减小，后验概率会增大
在这个例子中，如果我们考虑到窗户碎了、门开着、笔记本电脑不见了这些数据，如果这些事件的发生概率较小，实际上是暗示了一种情况：即这些事件同时发生的可能性较低。这种情况下，考虑到这些数据，可以得出两种可能性：

这些事件的发生是一个意外或者自然事件导致的，比如窗户可能是被风吹坏的，门可能是被人忘记关上的，笔记本电脑可能是被误放在别处。
这些事件的发生是有人为因素导致的，比如入室盗窃。

现在，这里涉及到一个问题是，如果我们假设入室盗窃这种事件的先验概率较低（即我们的先验信念是认为入室盗窃的可能性不大），那么即使考虑到这些数据，我们得到的后验概率可能也不会大到令人信服的程度。换句话说，即使考虑到这些事件，我们仍然更倾向于认为是意外事件造成的可能性更大。

所以，发生的数据概率较小不一定就意味着被盗的后验概率会高，这取决于我们对事件的先验信念以及我们考虑到的具体数据所提供的支持程度。
但有的时候P(D)很难精确计算，我们可以提出一个备择假设，计算它的后验概率，然后将其与原始假设的后验概率进行比较。

3. 考虑备择假设

现在提出另外一个假设，并将它与原来的假设进行比较。新假设包括以下3个事件。(1) 邻居家孩子把棒球打到了窗户上。(2) 你离开家时忘了锁门。(3) 你忘了自己带笔记本计算机去上班并把它落在了办公室。
我们用事件前面的编号来指代这些事件，并将它们统称为H2，所以P(H2)=P(1,2,3)。现在求解这些数据的似然和先验概率。