"The harder you work for something, the greater you'll feel when you achieve it." - Unknown

1. 题目描述
2. 题目分析与解析
2.1 思路一——暴力求解
该思路很简单,就是暴力的查找每一个元素,查看是否满足题目要求,满足就返回true,不满足就返回false。
代码思路:
-
一层for循环遍历每个
abs(i - j) <= k中的被减数 -
二层for循环遍历每个
abs(i - j) <= k中的减数 -
判定是否满足条件
效果果然如预期:
2.2 思路二——哈希表
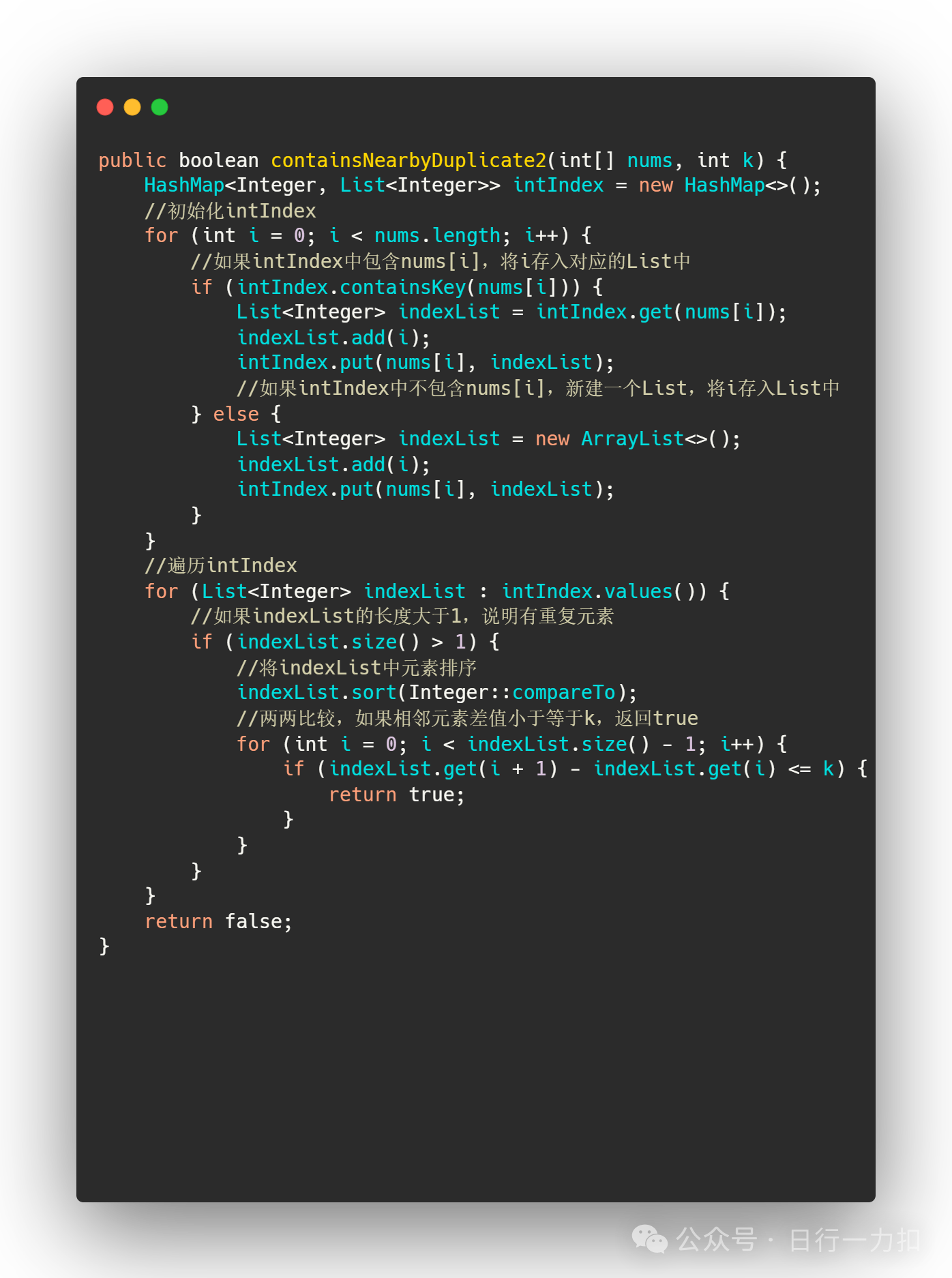
对于这种题目,因为题目要求 abs(i - j) <= k,它的前提是不同的索引 i 和 j ,满足 nums[i] == nums[j]。那么我们是不是就可以先把那些相同值的组存储起来,然后再寻找这些相同值的组中满足abs(i - j) <= k的进行计算?
如何存储相同值的组?
可以使用一个hashMap,键为每一个数组,值为其对应出现的下标的集合。
然后就可以通过遍历hashMap的每一个键,寻找其对应的值的元素个数大于等于两个的部分,然后再对这个部分排序(也就是下标进行排序),然后两两相减查看是否满足条件abs(i - j) <= k。
代码思路:
-
定义一个hashMap,键位数组所有不相同的元素,值为其出现下标的集合
-
遍历hashMap的每一个键,寻找其对应的值的元素个数大于等于两个的部分
-
对该部分先进行排序,然后两两相减查看是否满足条件
abs(i - j) <= k
之所以只需要两两相减,是因为我们需要找到的是abs(i - j)的最小值,因为如果最小值都不能满足 <= k,那么其它的肯定也不能满足。而最小值肯定就在排序后的两两之间,因为如下:
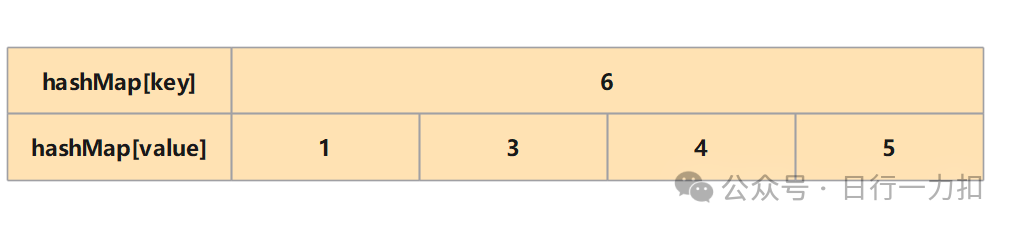
假如键位 6,对应出现的下标为 {1,3,4,5},那么肯定 abs(i - j)的最小值出现在 {3 - 1,4 - 3,5 - 4}其中。(代码见后3.2)
但是这样写出的代码发现并不是很能打,因为我们相当于遍历了两次所有元素,能否只遍历一次呢?
我们先来思考一下上面遍历两次是哪两次:
-
初始化hashMap
-
遍历hashMap
因为我们需要的是判断相同元素的下标相减的绝对值是否<=k,那么我们是不是可以在初始化hashMap的时候,就对每一个hashMap的值进行判断:
-
如果当前hashMap包含了该key,那么我们就进行判定是否满足
abs(i - j) <= k -
如果当前hashMap不包含该key,那就先把它加入hashMap
这样做的正确性是因为对于hashMap包含了该key的情况,说明该元素是第二次出现了,只需要将这两个元素的下标相减即可,并且对于hashMap的value我们也不需要存储所有相同元素的下标。这是因为记住我们创建这个hashMap的目的是什么,就是寻找最小的 abs(i - j),那么我们就可以通过定义一个变量,保存最小值,不断更新直到满足 <=k即可。
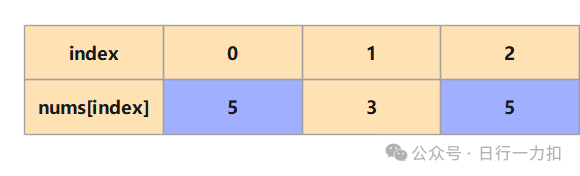
而hashMap的value,就可以存储上一次出现该元素的下标,这样在下一次遇到相同元素,离他最近的肯定是上一个相同元素的位置:

比如上图对于元素5,当遍历到下标2时,最小abs值是2,因为此时走过的元素中离下标2最近且元素值相等的 2 - 0 = 2 此时如下:
当继续遍历到下标3的时候,最小abs值就可以被更新为1:
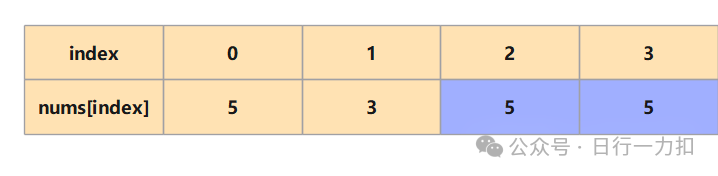
所以按照如上思路我们就可以将代码进行优化:
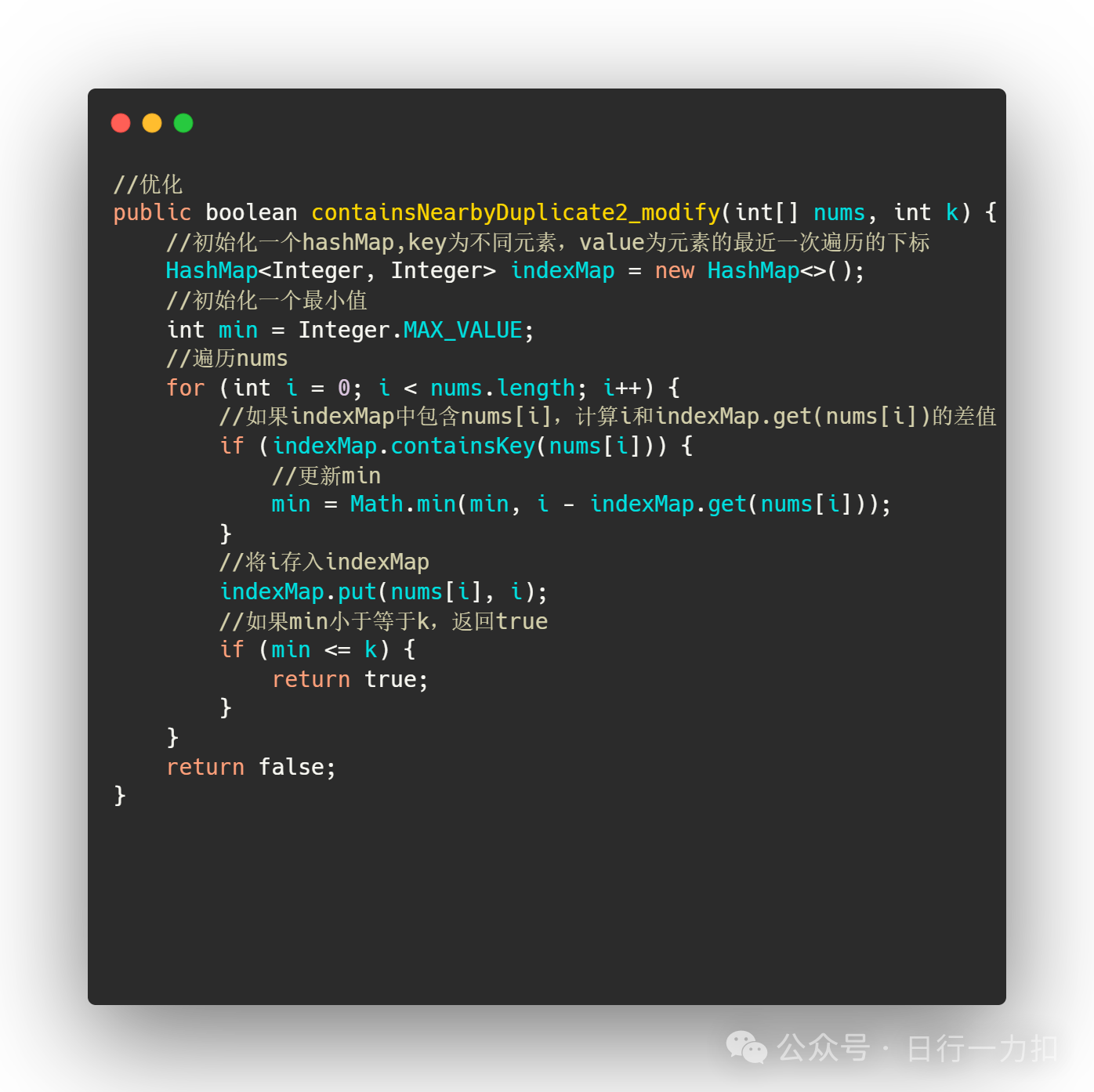
优化代码思路:
-
初始化一个hashMap,key为不同元素,value为元素的最近一次遍历的下标
-
初始化一个最小值
-
遍历nums
-
如果indexMap中包含nums[i],计算i和indexMap.get(nums[i])的差值并更新min
-
将当前值存入hashMap
-
如果min小于等于k,返回true
-
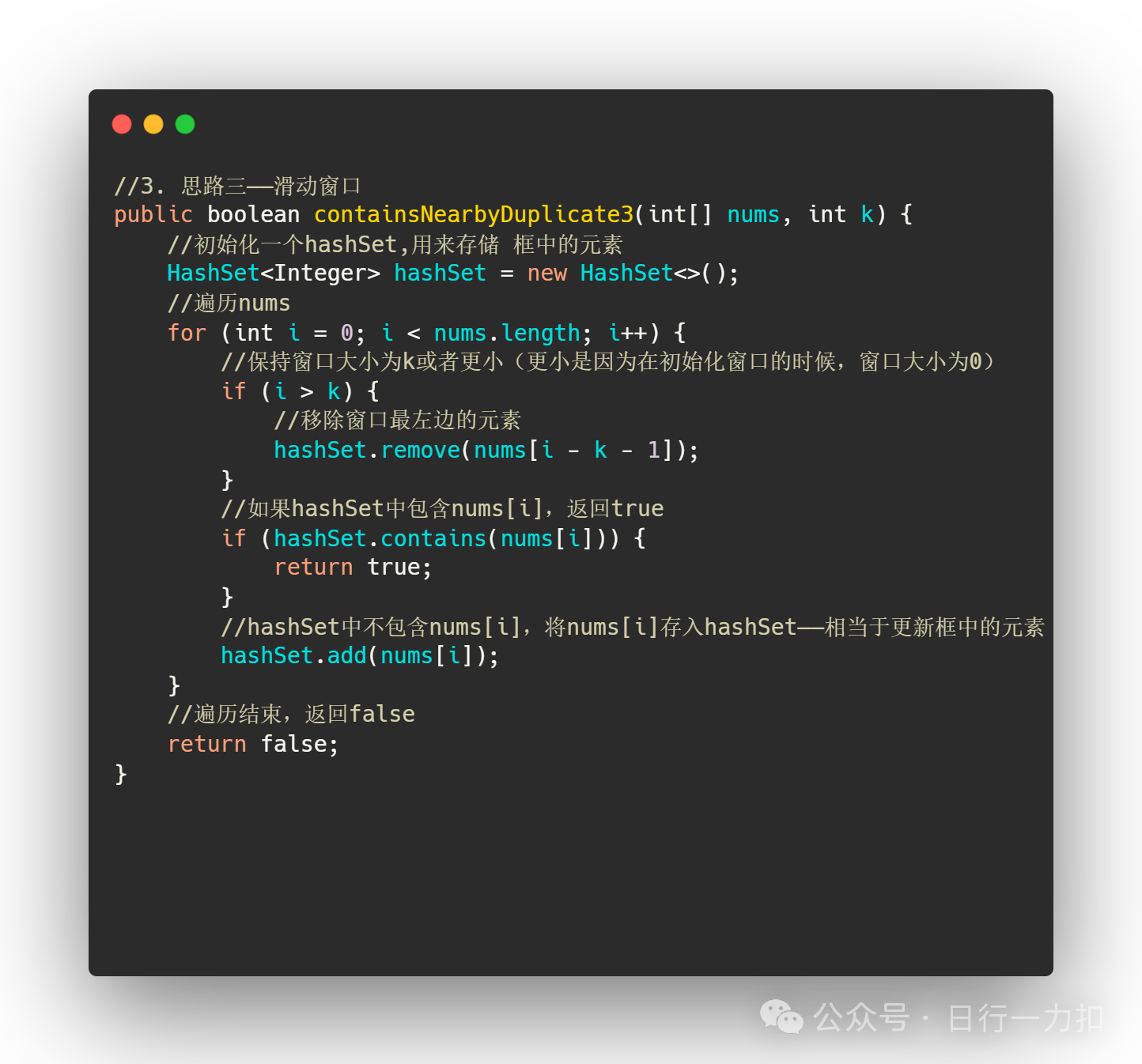
2.3 思路三——滑动窗口
因为我们要得到的结果只是一个布尔值,也就是真或者假,其它任何信息我们都不需要知道,只需要知道是否存在两个相同元素的下标之差的绝对值 <=k。
既然是下标之差的绝对值 <=k,那么是不是也就意味着在k+1(因为是小于等于,有等于情况所以需要+1)个相邻元素范围内,需要找到两个相同值的元素?只要找到了,那就说明存在可行解,就可以返回true,否则就返回false。比如如下对于:
![]()
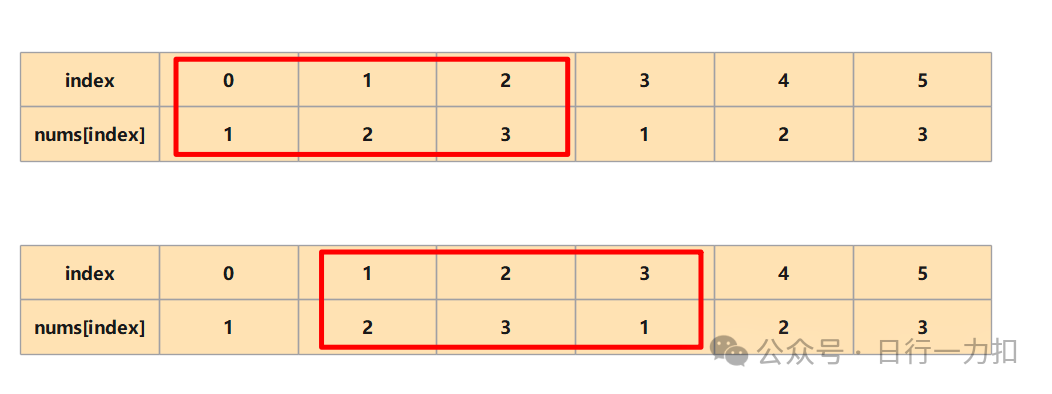
如上图所示,红色框就是一次次的判定k+1个相邻元素范围内,能否找到两个相同值的元素,这样不断判定直到结尾:
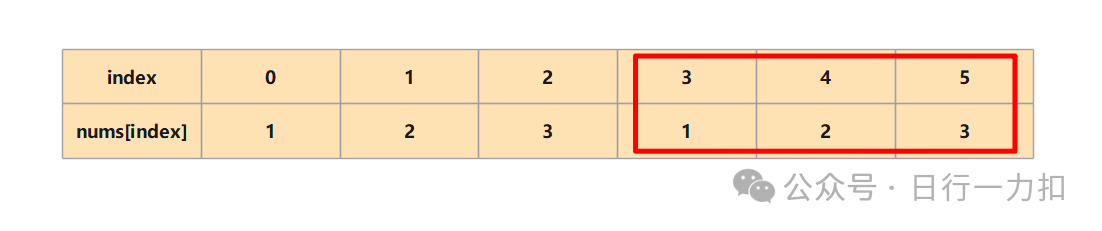
发现都没有满足那就返回false。
所以我们现在来思考如何判定k+1个相邻元素范围内,能否找到两个相同值的元素?
那我们还是可以借鉴前面的思想,就是用一个hashSet存储k+1个相邻元素的值作为键,不断去判断下一个遍历的值是否在这个红色框中,
-
如果当前元素下标小于等于k说明,判定该元素是否在框内,如果不在就向框中加入该元素,在就返回true(这是因为在初始化窗口的时候,窗口大小为0)
-
如果发现当前元素下标大于k了,也就是刚开始位k+1的时候,需要移除窗口最左边的元素,因为此时窗口大小要保持k+1
-
如果此时hashSet中包含了当前元素nums[i],返回true
-
如果遍历到了结尾还是没有返回true,就说明不存在解返回false
3. 代码实现
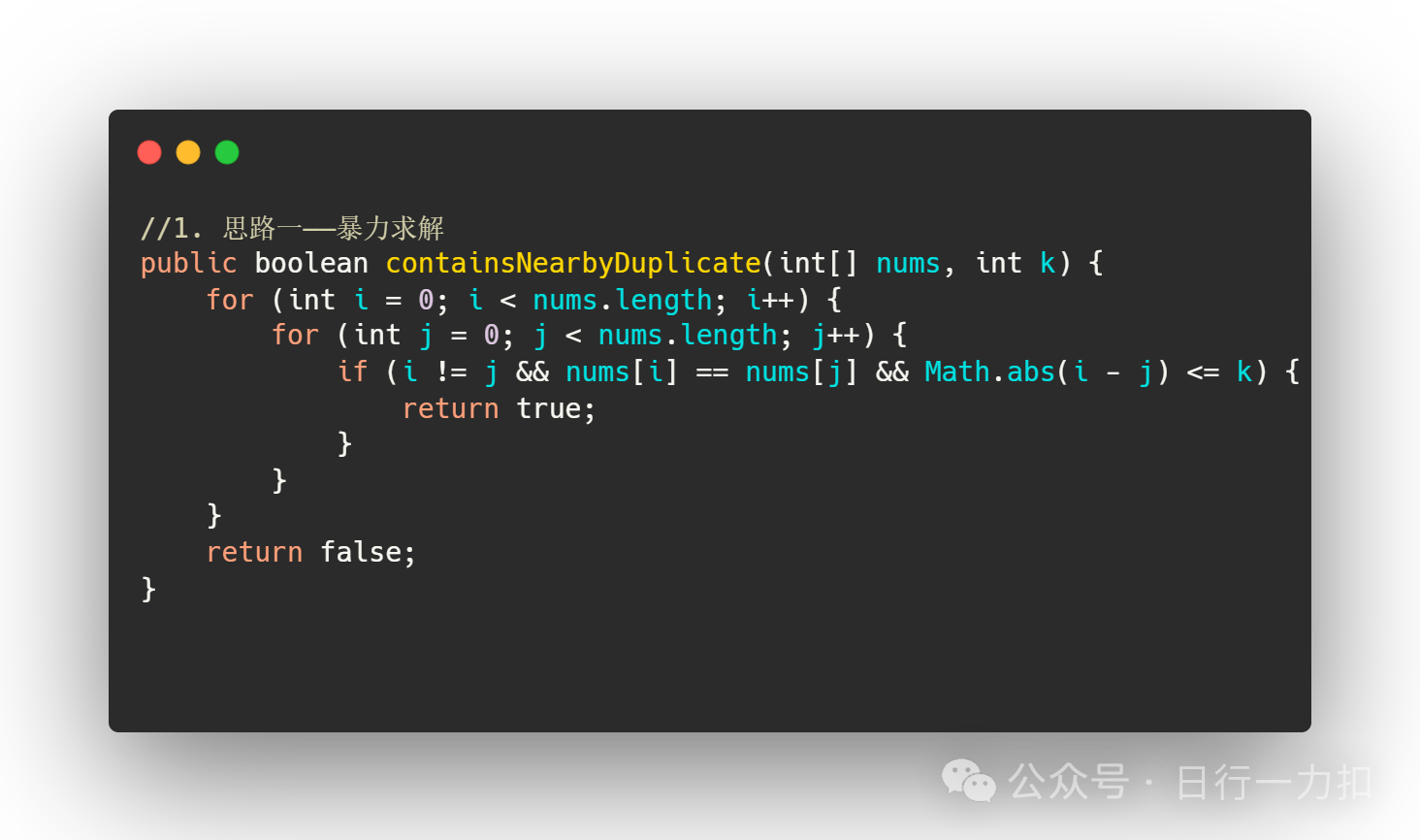
3.1 思路一——暴力求解
3.2 思路二——哈希表
经过优化以后:
3.3思路三——滑动窗口
4. 相关复杂度分析
1. 暴力求解方法 (containsNearbyDuplicate)
-
时间复杂度: O(n^2) - 这是因为对于数组中的每个元素,代码都进行了一个内部循环来比较所有其他元素。对于长度为n的数组,这就导致了n*(n-1)/2次比较。
-
空间复杂度: O(1) - 由于不需要额外存储空间,除了输入数组和几个变量外,这个方法不占用额外的空间。
2.1 哈希表方法 (containsNearbyDuplicate2)
-
时间复杂度: O(n log n) - 这个复杂度主要来自于为每个元素的索引列表进行排序的需求。在最坏的情况下,如果所有元素都相同,则每个元素都会被添加到同一个列表中,对这个列表排序的时间复杂度为O(n log n)。
-
空间复杂度: O(n) - 在最坏的情况下,如果所有的元素都不同,则
HashMap将会存储n个键值对,每个键对应一个只含有一个元素的列表。
2.2 哈希表方法优化 (containsNearbyDuplicate2_modify)
-
时间复杂度: O(n) - 对于每个元素,只需要O(1)的时间来更新哈希表,并检查当前元素与之前出现的元素之间的距离。
-
空间复杂度: O(n) - 哈希表在最坏的情况下可能需要存储n个键值对,即数组中的每个元素都不相同。
3. 滑动窗口方法 (containsNearbyDuplicate3)
-
时间复杂度: O(n) - 数组中的每个元素都被访问一次。对于每个元素的访问,检查元素是否在
HashSet中以及添加和删除操作都可以在O(1)时间内完成。 -
空间复杂度: O(min(n, k)) - 滑动窗口方法中,
HashSet的大小由窗口的最大大小k决定,但不会超过n(数组的长度)。在最坏的情况下,如果k大于或等于n,那么空间复杂度将是O(n);如果k小于n,空间复杂度是O(k)。