3046. 分割数组 简单

3046. 分割数组

分析：
查看数组内有没有重复超过2次的数即可。

代码：

class Solution {
public:bool isPossibleToSplit(vector<int>& nums) {unordered_map<int,int> m;for(int& num : nums){m[num]++;if(m[num]>2) return false;}return true;}
};

3047. 求交集区域内的最大正方形面积 中等

3047. 求交集区域内的最大正方形面积

分析：
枚举两个正方形，判断是否有交集。
下图为两个存在相交面积的正方形，其对应边的坐标如下图。

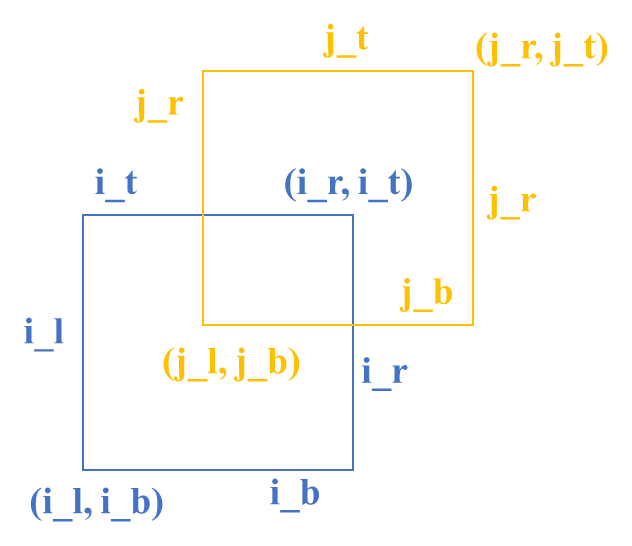
注意：

• 取得是交集区域内的正方形面积，因此只需要去最小边长即可。
• 注意没有交集时，最小边长为 0。

代码：

class Solution {
public:long long largestSquareArea(vector<vector<int>>& bottomLeft, vector<vector<int>>& topRight) {int n = bottomLeft.size(),ans=0;for(int i=0;i<n;i++){for(int j=i+1;j<n;j++){int i_b=bottomLeft[i][1],i_l=bottomLeft[i][0],i_t=topRight[i][1],i_r=topRight[i][0];int j_b=bottomLeft[j][1],j_l=bottomLeft[j][0],j_t=topRight[j][1],j_r=topRight[j][0];int b=max(i_b, j_b),l=max(i_l, j_l),t=min(i_t, j_t),r=min(i_r, j_r);ans = max(ans,min(max(t-b, 0), max(r-l, 0)));}}return 1LL*ans*ans;}
};

3048. 标记所有下标的最早秒数 I 中等

3048. 标记所有下标的最早秒数 I

分析：
若要判断 m 的时间是否能完成

• 1、判断1...m是否出现了所有的下标
• 2、根据每个下标最后出现的先后顺序进行判断，假设前面全是该下标的 nums[i] 减小1，以及先出现的下标的 nums[j] 减小1和 j 的标记，判断该情况下是否能标记。

对于m我们能判断，此时我们可以利用二分来寻找最小的能标记所有下标的秒数。

代码：

class Solution {
public:int earliestSecondToMarkIndices(vector<int>& nums, vector<int>& changeIndices) {int n=nums.size(), m=changeIndices.size();auto check = [&](int k) -> bool{int cnt = 0;vector<int> index(n,-1);for(int i=0;i<k;i++){int t = changeIndices[i];if(index[t-1]==-1) cnt++;index[t-1]=i;}if(cnt<n) return false;vector<pair<int,int>> p;for(int i=0;i<n;i++){p.push_back({index[i],i});}sort(p.begin(),p.end(),[](pair<int, int>& a, pair<int, int>& b){return a.first < b.first;});int last = -1, remain = 0;for(int i=0;i<n;i++){int id = p[i].second, cid = p[i].first, c = nums[id];if(cid - last - 1 + remain < c) return false;remain = cid - last - 1 + remain - c, last = cid;}return true;};int l=1, h=m, ans=-1, mid;while(l<=h){mid = (l+h)/2;if(check(mid)) h=mid-1, ans=mid;else l=mid+1;}return ans;}
};