LeetCode343.整数拆分
题目描述:
给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),并使这些整数的乘积最大化。
返回 你可以获得的最大乘积 。
示例 1:
输入: n = 2 输出: 1 解释: 2 = 1 + 1, 1 × 1 = 1。
示例 2:
输入: n = 10 输出: 36 解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
解题思路:
1.确定dp数组以及其下标的含义
dp[i]:拆分数字i,可以得到的最大乘积为dp[i]
2.确定递推公式
需要明确的是dp[i]的最大乘积是如何得到的,从1开始遍历,有两个方法可以得到dp[i]
一个是j*(i-j),也就是将数拆成两个数
一个是j*dp[i-1],也就是将数拆成两个以上的数,如果不能理解,可以看看我们队dp[i]的定义
所以递推公式就得到了dp[i] = max(dp[i],max((i-j)*j,dp[i-j]*j))
3.dp数组如何初始化
依旧从定义出发,我们就可以知道,dp[i]初始化最小要从2开始,因为按照我们的定义,如果i等于0或者1,那么就没有任何意义(因为dp[i]是可以拆分的数的乘积)
那么我就将dp[2]赋值为1
4.确定遍历顺序
根据递推公式,我们可以知道,dp[i]的结果需要知道dp[i-j],所以我们的结果是需要从前向后推导的
5.举例推导dp数组
因为这道题的计算量比较大,所以,我们只能以示例为例子,观察是否可以得到正确的答案
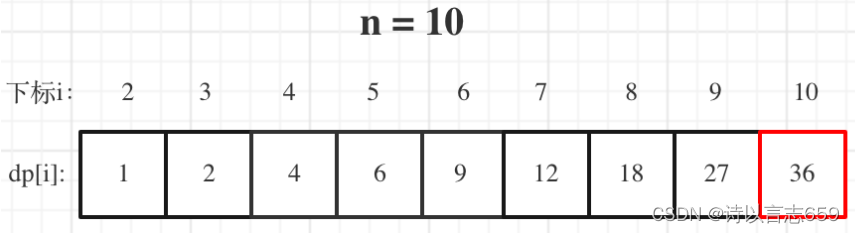
以上分析完毕,代码如下:
class Solution {
public:int integerBreak(int n) {vector<int> dp(n+1);dp[2] = 1;for(int i = 3;i <= n;i++){for(int j = 1;j <= i/2;j++){dp[i] = max(dp[i],max((i-j)*j,dp[i-j]*j));}}return dp[n];}
};·时间复杂度:O(n^2)
·空间复杂度:O(n)
难点:
·递推公式的推导
·dp[i]初始值的确定
总结
这道题的递推公式并不好想,而且初始化的时候,也有很多细节的地方,而且一切都需要围绕着dp[i]的定义推导,否则就会出现自相矛盾的地方
LeetCode96.不同的二叉搜索树
题目描述:
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:
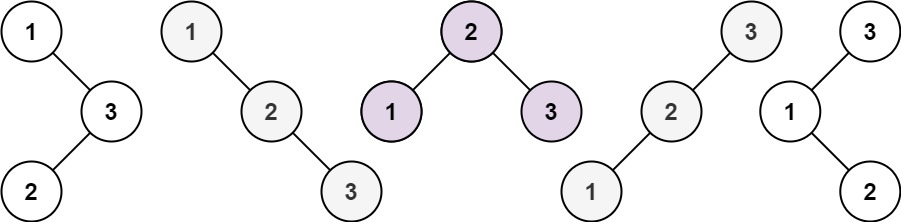
输入:n = 3 输出:5
示例 2:
输入:n = 1 输出:1
解题思路:
1.确定dp数组以及其下标的含义
dp[i]:1到i为节点组成的二叉搜索树的个数为dp[i]
也可以理解为i个不同元素节点组成的二叉搜索树的个数为dp[i]
2.确定递推公式
这题的递推公式比较复杂,需要从例题中一点一点分析出来
当n为1的时候,只有一颗搜索树
当n为2的时候,有两颗搜索树
当n为3的时候,其左子树有两个节点并且这两个节点的布局,与n为2时的情况一致
当n为1的时候,其右子树的两个节点也与n为2时的情况一致
当n为2时,其左右子树都只有一个节点,可以看作是与n为1时的情况一致
分析到此,我们就找到了重叠子问题,并且可以发现,dp[3]是由dp[1]和dp[2]推导而来
dp[3]= 以元素1为根节点搜索树的数量+以元素2为根节点搜索树的数量+以元素3为根节点搜索树的数量
以元素1为根节点搜索树的数量 = 右子树2个元素的搜索树数量*左子树有0个元素的搜索树的数量
以元素2为根节点搜索树的数量 = 右子树1个元素的搜索树数量*左子树有1个元素的搜索树数量
以元素3为根节点搜索树的数量 = 右子树0个元素的搜索树数量*左子树有2个元素的搜索树数量
所以dp[3] = dp[2]*dp[0] + dp[1]*dp[1] + dp[0]*dp[2]
所以从以上分析可知,dp[i] += dp[以j为根结点左子树节点数量]*dp[以j为根结点右子树节点数量]
j相当于是根节点的元素,遍历从1到i为止
所以递推公式为 dp[i] += dp[j-1]*dp[i-j];j-1为根结点左子树数量,i-j为以j为根节点右子树数量
3.dp数组如何初始化
只需要初始化dp[0]即可,因为空结点也算是一棵二叉树,并且属于n为1的左右子树,可以推导出dp[1],但是千万不能赋值为0,否则无法得到数值
4.确定遍历顺序
从递推公式就可以看出,节点数为i的状态是依靠之前节点数的状态
那么遍历中i需要从头遍历,再使用j遍历到i,剩下的则作为其右子树
5.举例推导dp数组
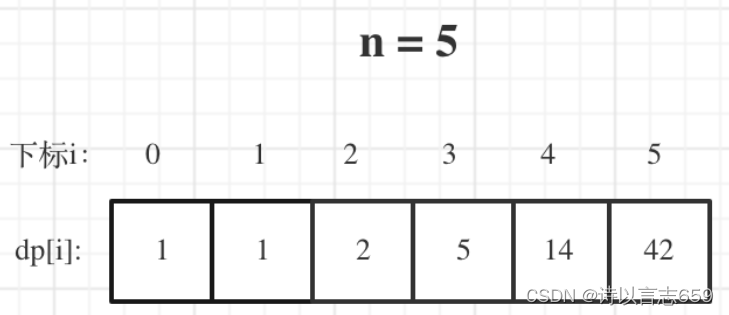
递推到3或者4就足够了,n为5的时候数量已经很大了
综上分析,代码如下:
class Solution {
public:int numTrees(int n) {vector<int> dp(n+1);dp[0] = 1;for(int i = 1;i <= n;i++){for(int j = 1;j <= i;j++){dp[i] += dp[j-1]*dp[i-j];}}return dp[n];}
};·时间复杂度:O(n^2)
·空间复杂度:O(n)
难点:
·递推公式的确定
·初始值的赋予
·遍历顺序,尤其是j的遍历
总结
这道题使用动态规划是比较复杂的,因为需要举例,分析,才能找到递推关系
然后就是递推公式,如果把递推公式想明白了,那么遍历顺序和初始化,就是顺其自然的可以得出
所以按照递归五部曲可以准确的解决动态规划的题目,大家可能已经初步感受到了五部曲带来的好处