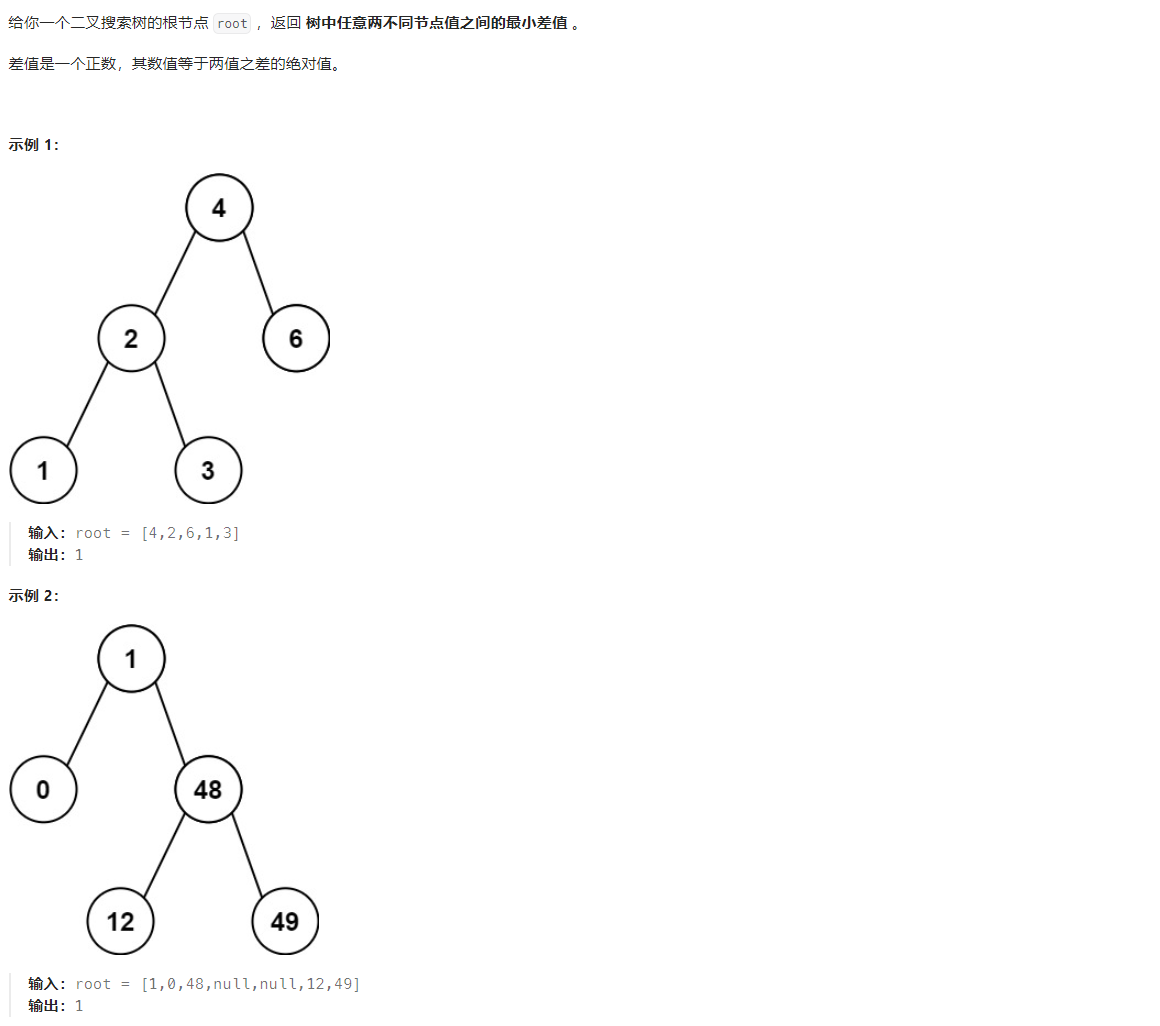
因为二叉搜索树的中序遍历是有序的，所以在中序递归遍历的基础上，记录前一个节点的指针，递归的过程中用后一个节点减去前一个，就可以得到差值，保存最小差值并返回。
代码如下：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
private: vector<int> vec;int result = INT_MAX;TreeNode* pre = nullptr;void traversal(TreeNode* node) {if(node == nullptr) return;traversal(node->left);if(pre != nullptr) {result = min(result, node->val - pre->val);}pre = node;traversal(node->right);}
public:int getMinimumDifference(TreeNode* root) {traversal(root);return result;}
};

还是根据二叉搜索树的中序遍历是有序的，所以在递归中序遍历中记录重复出现次数，下面我们主要探究如何记录。
先定义一个前指针，判断前指针和当前指针相同则count++。
这时有一个问题，众数不止一个，所以我们还需要记录 当前众数的最大次数maxCount，当出现第二个元素等于maxCount，将此元素也放入众数集合，如果出现一个元素大于当前maxCount，还需要清空众数集合，并且更新最大次数。
代码如下：

class Solution {
private:int maxCount = 0; // 最大频率int count = 0; // 统计频率TreeNode* pre = NULL;vector<int> result;void searchBST(TreeNode* cur) {if (cur == NULL) return ;searchBST(cur->left);       // 左// 中if (pre == NULL) { // 第一个节点count = 1;} else if (pre->val == cur->val) { // 与前一个节点数值相同count++;} else { // 与前一个节点数值不同count = 1;}pre = cur; // 更新上一个节点if (count == maxCount) { // 如果和最大值相同，放进result中result.push_back(cur->val);}if (count > maxCount) { // 如果计数大于最大值频率maxCount = count;   // 更新最大频率result.clear();     // 很关键的一步，不要忘记清空result，之前result里的元素都失效了result.push_back(cur->val);}searchBST(cur->right);      // 右return ;}public:vector<int> findMode(TreeNode* root) {count = 0;maxCount = 0;pre = NULL; // 记录前一个节点result.clear();searchBST(root);return result;}
};

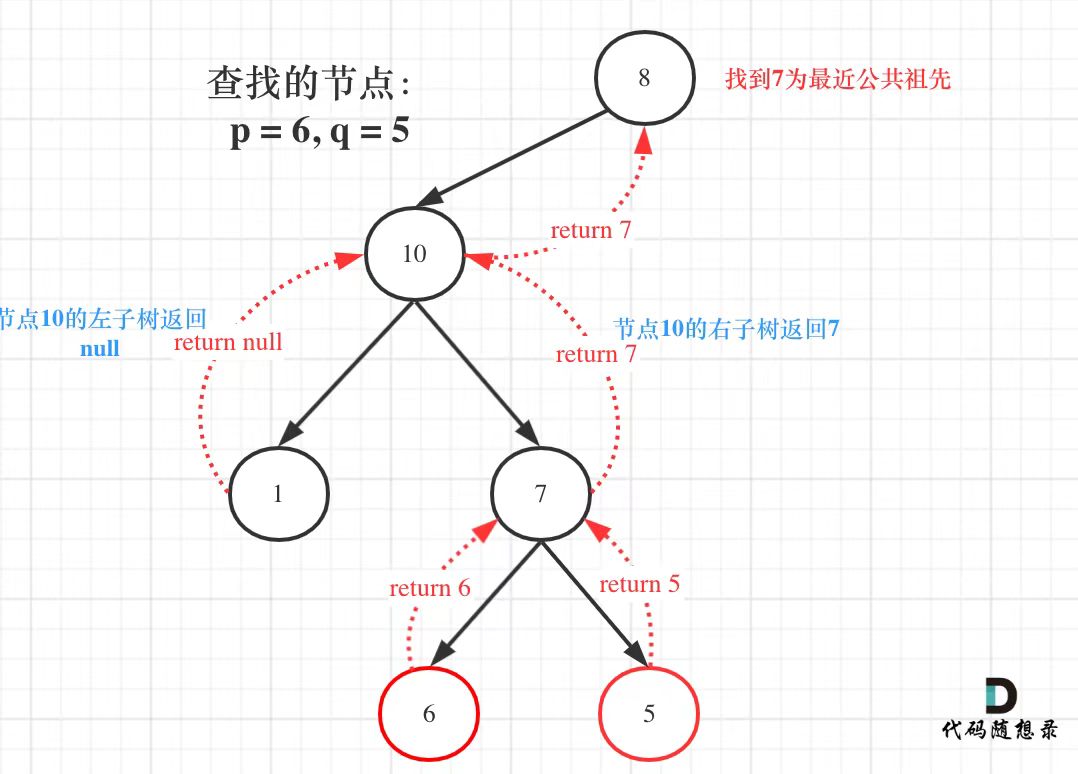
二叉树回溯的过程就是从低到上（后序遍历），刚好契合本题从下往上找最近公共祖先节点。
1.参数和返回值：TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q)
2.终止条件：找到q或者p或者遇到空节点返回。
3.单层递归逻辑：我们要遍历整个树，所以不能立刻返回。

class Solution {
public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {if (root == q || root == p || root == NULL) return root;//终止条件TreeNode* left = lowestCommonAncestor(root->left, p, q);//单层递归逻辑TreeNode* right = lowestCommonAncestor(root->right, p, q);if (left != NULL && right != NULL) return root;if (left == NULL && right != NULL) return right;else if (left != NULL && right == NULL) return left;else  { //  (left == NULL && right == NULL)return NULL;}}
};