文章目录
- 1. 136. 只出现一次的数字
- 题目详情
- 代码(直接来异或)
- 思路
- 2. 118. 杨辉三角
- 题目详情
- 代码1
- 思路
- 代码2
- 思路2
- 3. 26. 删除有序数组中的重复项
- 题目详情
- 代码
- 思路
- 4. JZ39 数组中出现次数超过一半的数字
- 题目详情
- 代码1(暴力)
- 思路1
- 代码2(Boyer-Moore 投票算法)
- 思路2
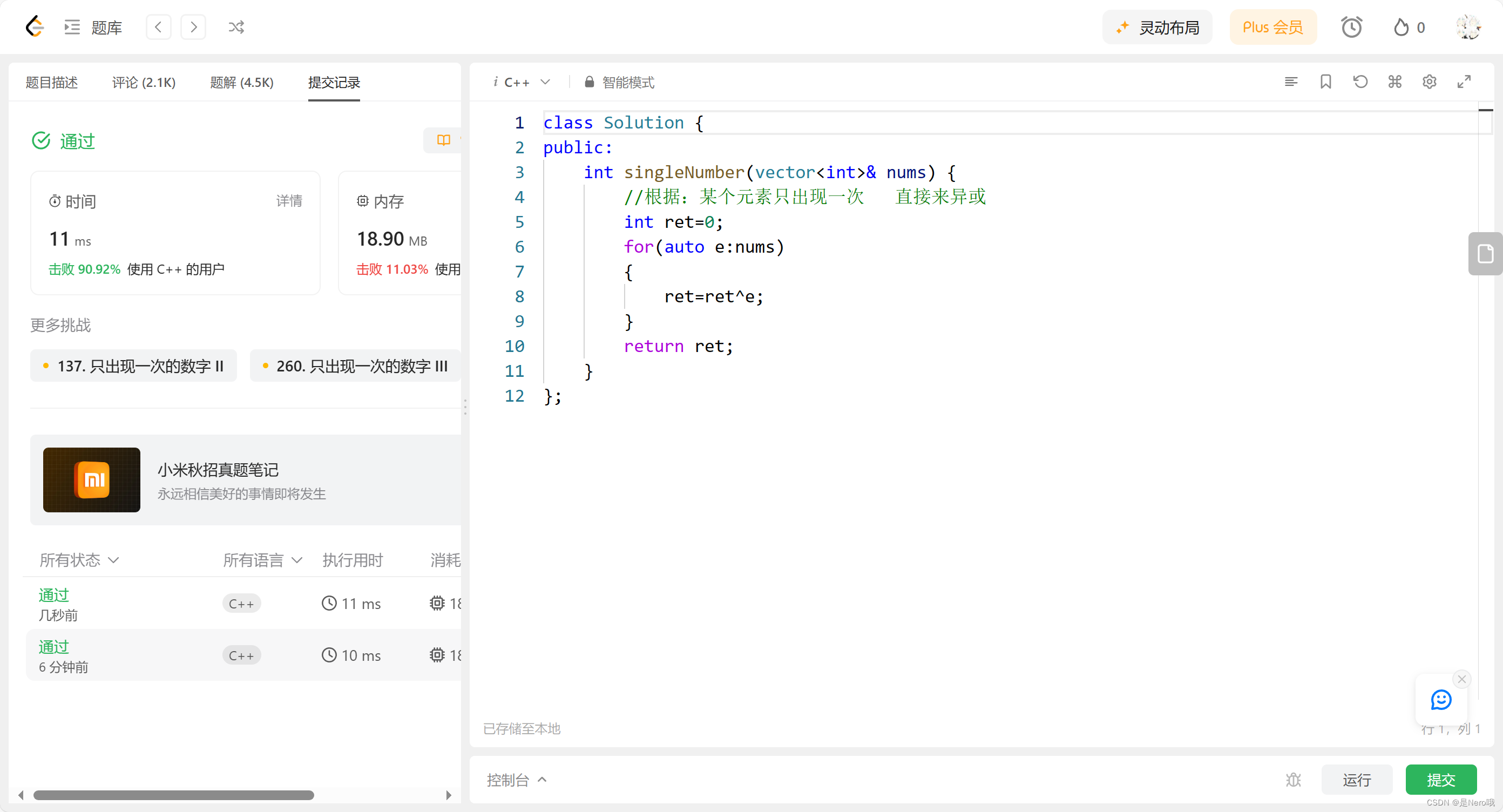
1. 136. 只出现一次的数字
传送门
题目详情

代码(直接来异或)
class Solution {
public:int singleNumber(vector<int>& nums) {//根据:某个元素只出现一次 直接来异或int ret=0;for(auto e:nums){ret=ret^e;}return ret;}
};
思路
- 异或运算的性质:异或运算(^)具有以下性质**(相同为0,相异为1)**
- 任何数和0做异或运算,结果仍然是原来的数:a ^ 0 = a
- 任何数和自身做异或运算,结果为0:a ^ a = 0
- 异或运算满足交换律和结合律:a ^ b ^ a = (a ^ a) ^ b = 0 ^ b = b
- 利用异或运算的性质:如果一个数出现两次,那么两次出现的数异或后结果为0;如果一个数只出现一次,那么异或后结果为该数本身。
- 利用上述性质,遍历
nums中的所有元素,并进行异或运算,最终得到的结果就是只出现一次的元素。
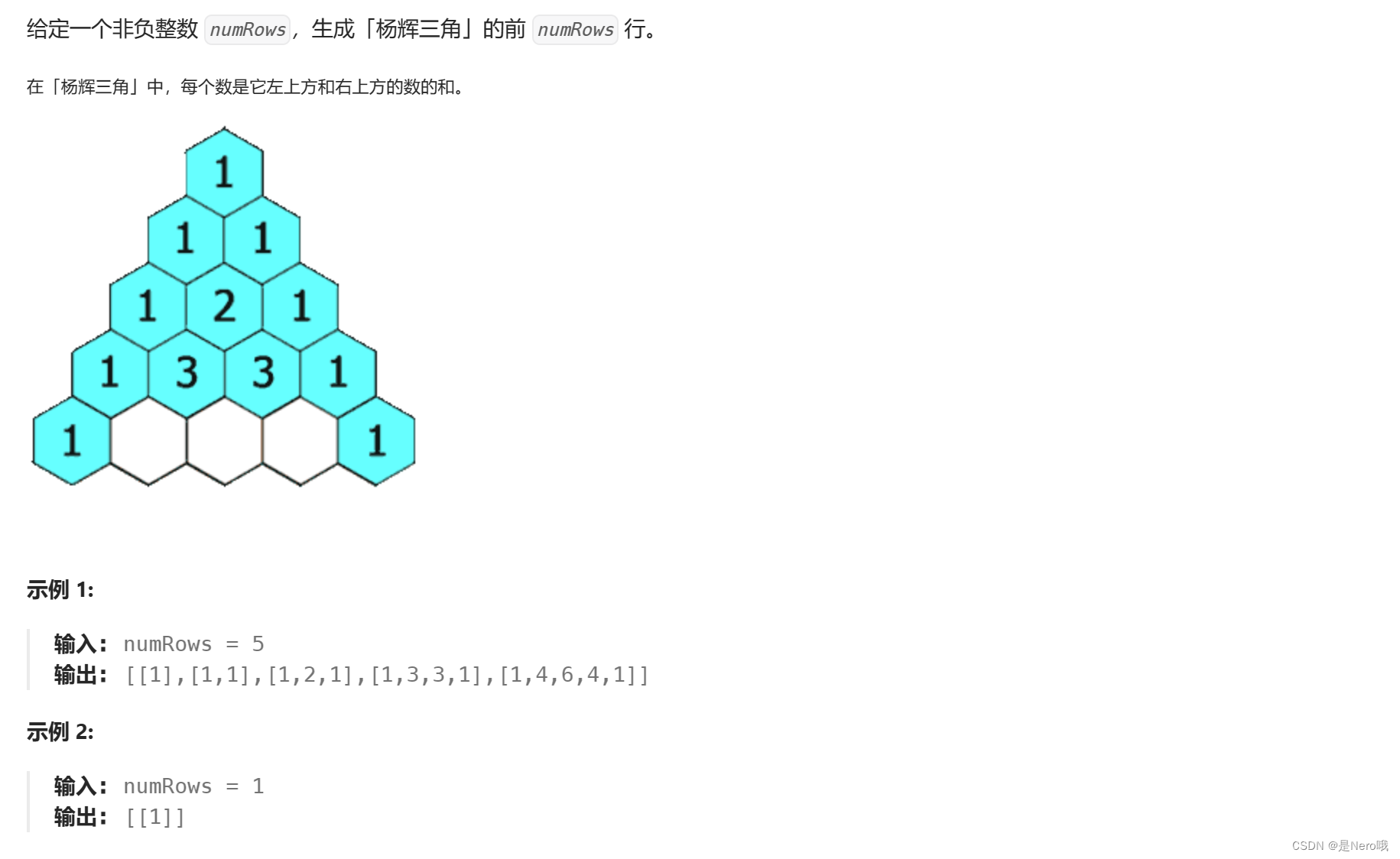
2. 118. 杨辉三角
传送门
题目详情
代码1
class Solution {
public:vector<vector<int>> generate(int numRows) {vector<vector<int>> vv;vv.resize(numRows);//先给好numRows个元素,即vv里能存vector<int>for(int i=0;i<numRows;i++)//对一行进行处理{vv[i].resize(i+1);//每一行里再开好对应的大小vv[i].front()=vv[i].back()=1;//最左最右都是1}for(int i=2;i<numRows;i++){for(int j=1;j<i;j++){vv[i][j]=vv[i-1][j-1]+vv[i-1][j];}}return vv;}
};
思路
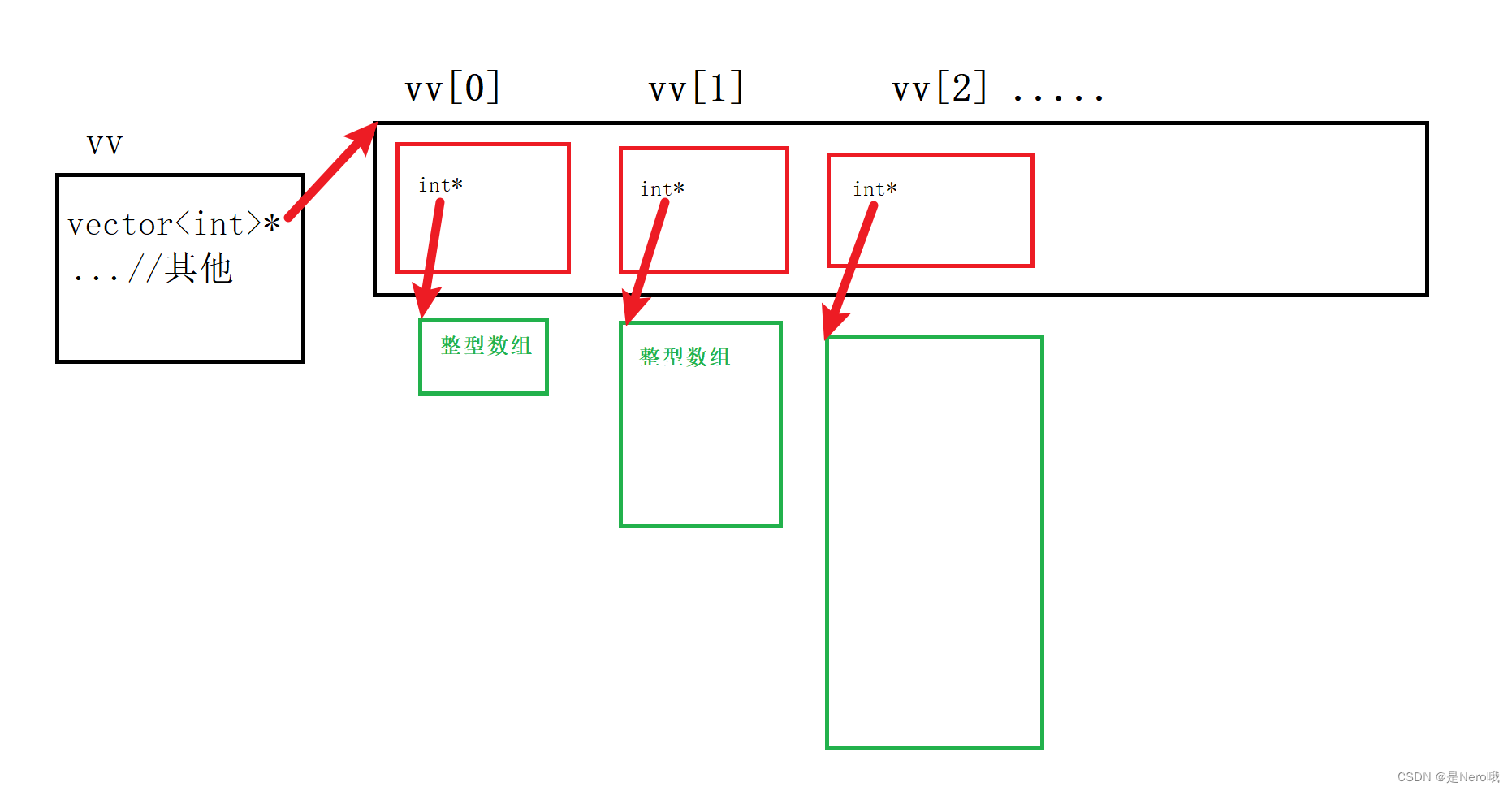
-
创建一个二维vector
vv,用于存储杨辉三角的数据。vv的第i行第j列的元素表示杨辉三角中第i行第j列的数值。 -
首先,通过
vv.resize(numRows)为vv分配了numRows个元素,即vv中可以存储numRows行的vector(即numRows个vector) -
对于每一行,通过
vv[i].resize(i+1)为其分配了合适的大小,即第i行有i+1个元素。(从0开始) -
对于每一行的第一个和最后一个元素,将其赋值为1,因为杨辉三角的每一行的两端都是1。
-
最后,对于第三行及以上的每一行,利用杨辉三角的性质,即第i行第j列的数值等于第i-1行第j-1列和第j列的数值之和,来计算每一行的中间元素的值。
例如,第i行第j列的元素等于第i-1行第j-1列和第i-1行第j列的元素之和,即
vv[i][j] = vv[i-1][j-1] + vv[i-1][j]。通过以上步骤,最终得到了杨辉三角的前
numRows行。
举个例子:
如果numRows为5,那么vv的内容将会是:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
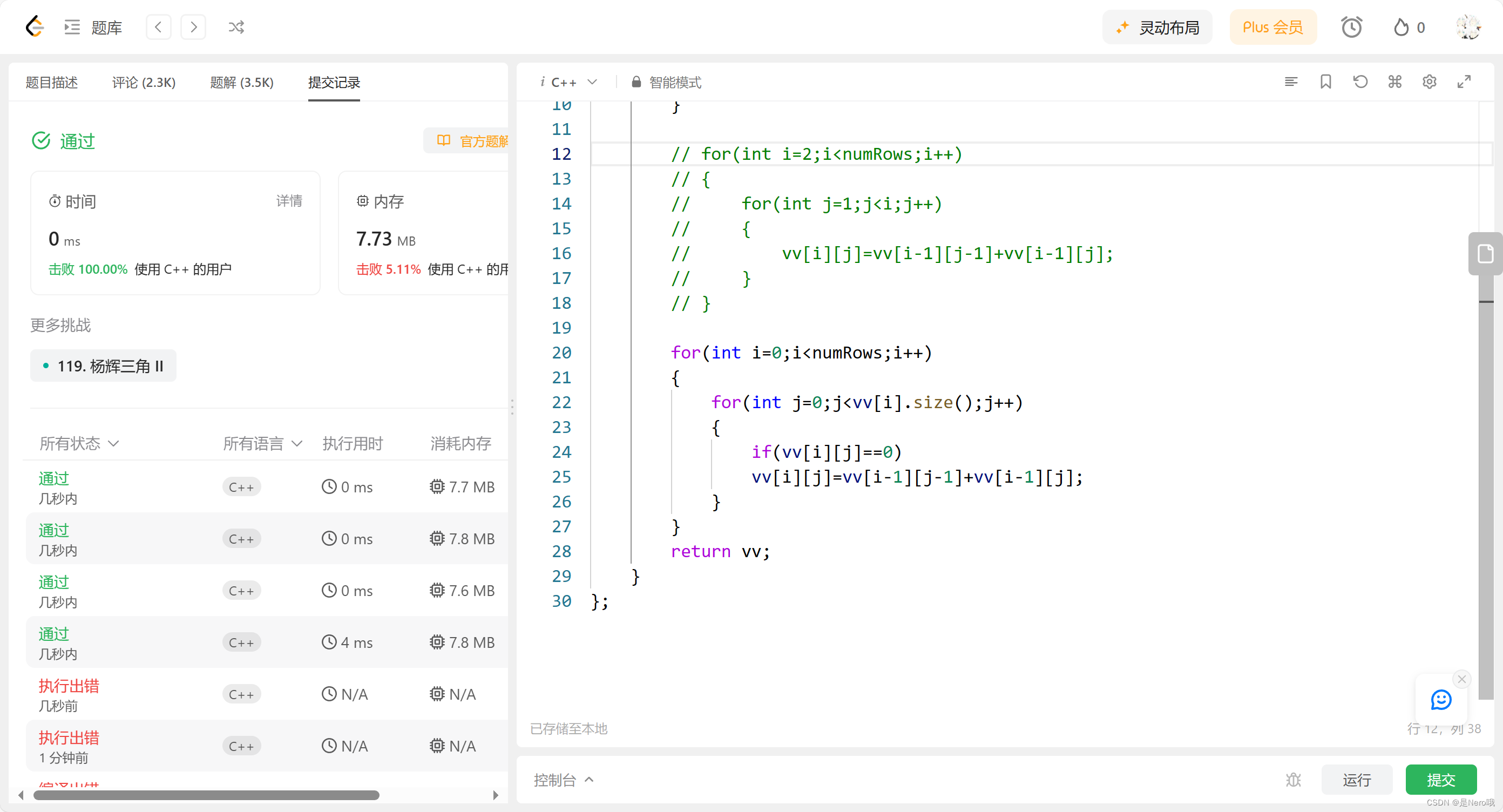
代码2
class Solution {
public:vector<vector<int>> generate(int numRows) {vector<vector<int>> vv;vv.resize(numRows);//先给好numRows个元素,即vv里能存vector<int>for(int i=0;i<numRows;i++)//对一行进行处理{vv[i].resize(i+1,0);//每一行里再开好对应的大小vv[i].front()=vv[i].back()=1;//最左最右都是1}for(int i=0;i<numRows;i++){for(int j=0;j<vv[i].size();j++){if(vv[i][j]==0)vv[i][j]=vv[i-1][j-1]+vv[i-1][j];}}return vv;}
};
思路2
大致都一样,不过在进行相加这里头和尾也都算上,因为在一开始开空间,全都给0了。
能多加一个条件判断,不怕越界
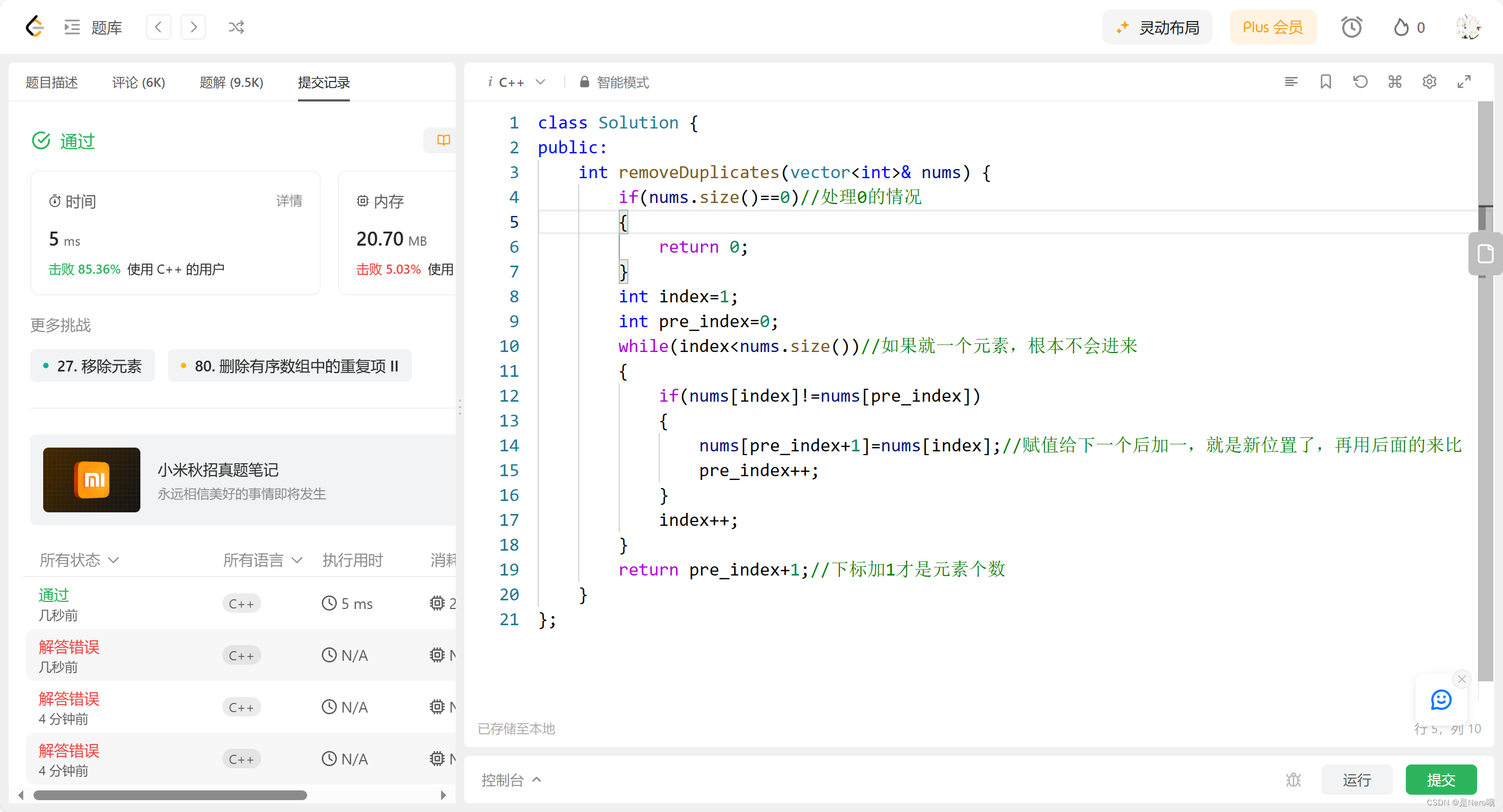
3. 26. 删除有序数组中的重复项
传送门
题目详情

代码
class Solution {
public:int removeDuplicates(vector<int>& nums) {if(nums.size()==0)//处理0的情况{return 0;}int index=1;int pre_index=0;while(index<nums.size())//如果就一个元素,根本不会进来{if(nums[index]!=nums[pre_index]){nums[pre_index+1]=nums[index];//赋值给下一个后加一,就是新位置了,再用后面的来比pre_index++;}index++;}return pre_index+1;//下标加1才是元素个数}
};
思路
这里需要注意,给出的数组是总体上是升序的
-
首先检查数组是否为空,如果是空数组则直接返回0,因为没有重复元素。
-
定义两个指针
index和pre_index,分别代表当前遍历的元素和上一个不重复元素的位置。index初始值为1,因为我们从第二个元素开始遍历;pre_index初始值为0,因为第一个元素肯定是不重复的 -
循环遍历数组,从第二个元素开始。如果当前元素与上一个不重复元素不相同,就将当前元素放在上一个不重复元素的下一个位置,并将
pre_index更新为当前的位置(新的不重复元素的位置) -
最后返回 pre_index+1,即为不重复元素的数量
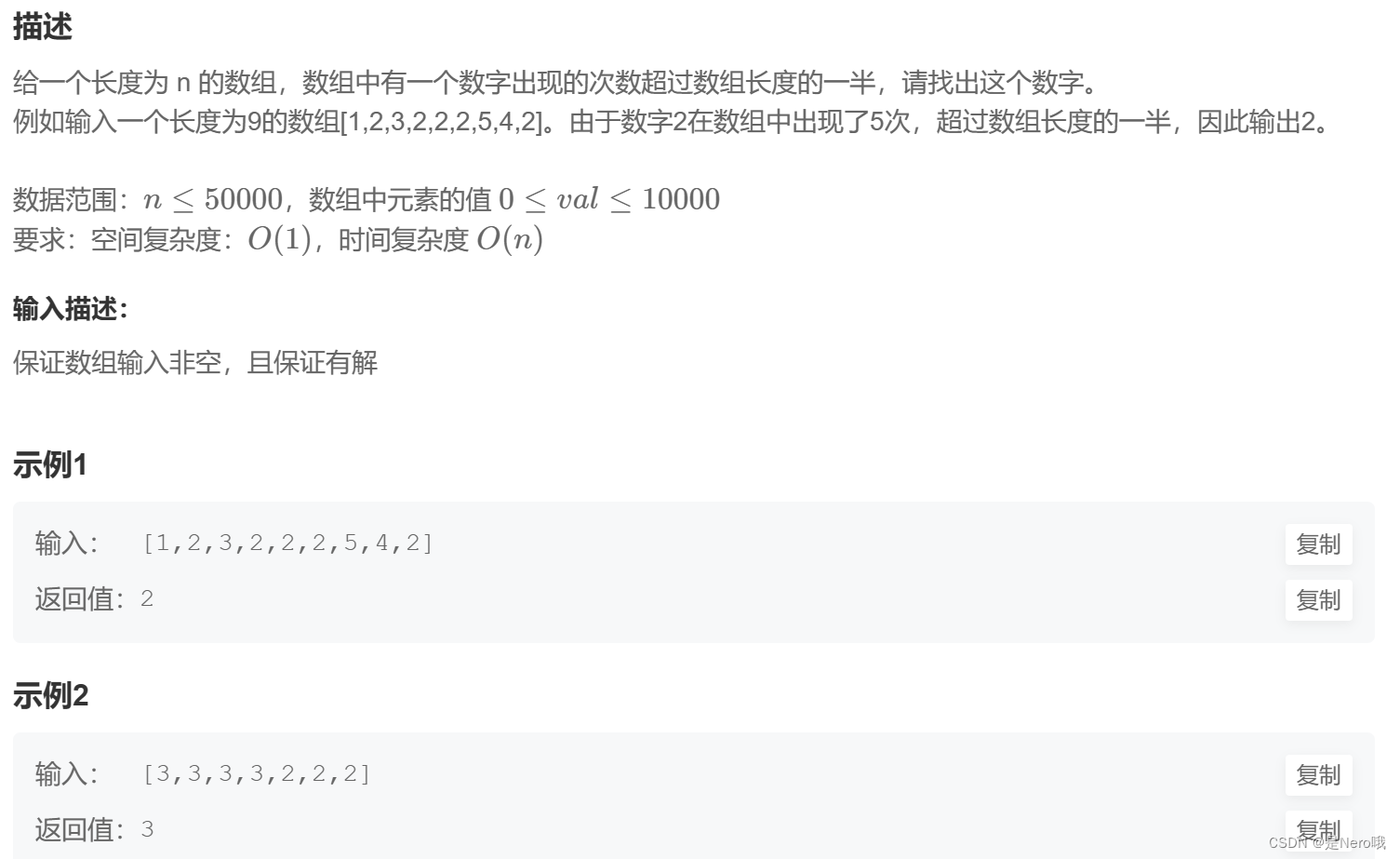
4. JZ39 数组中出现次数超过一半的数字
传送门
题目详情
代码1(暴力)
int MoreThanHalfNum_Solution(vector<int>& numbers) {// write code hereint half=numbers.size()/2;for(int i=0;i<numbers.size();i++){int count=0;for(int j=i+1;j<numbers.size();j++){if(numbers[i]==numbers[j]){count++;}if(count>=half){return numbers[i];}}}return numbers[0];}
};
思路1
暴力运用两次循环,对每个元素进行统计,大家都知道效率肯定很差。
下面看第二个
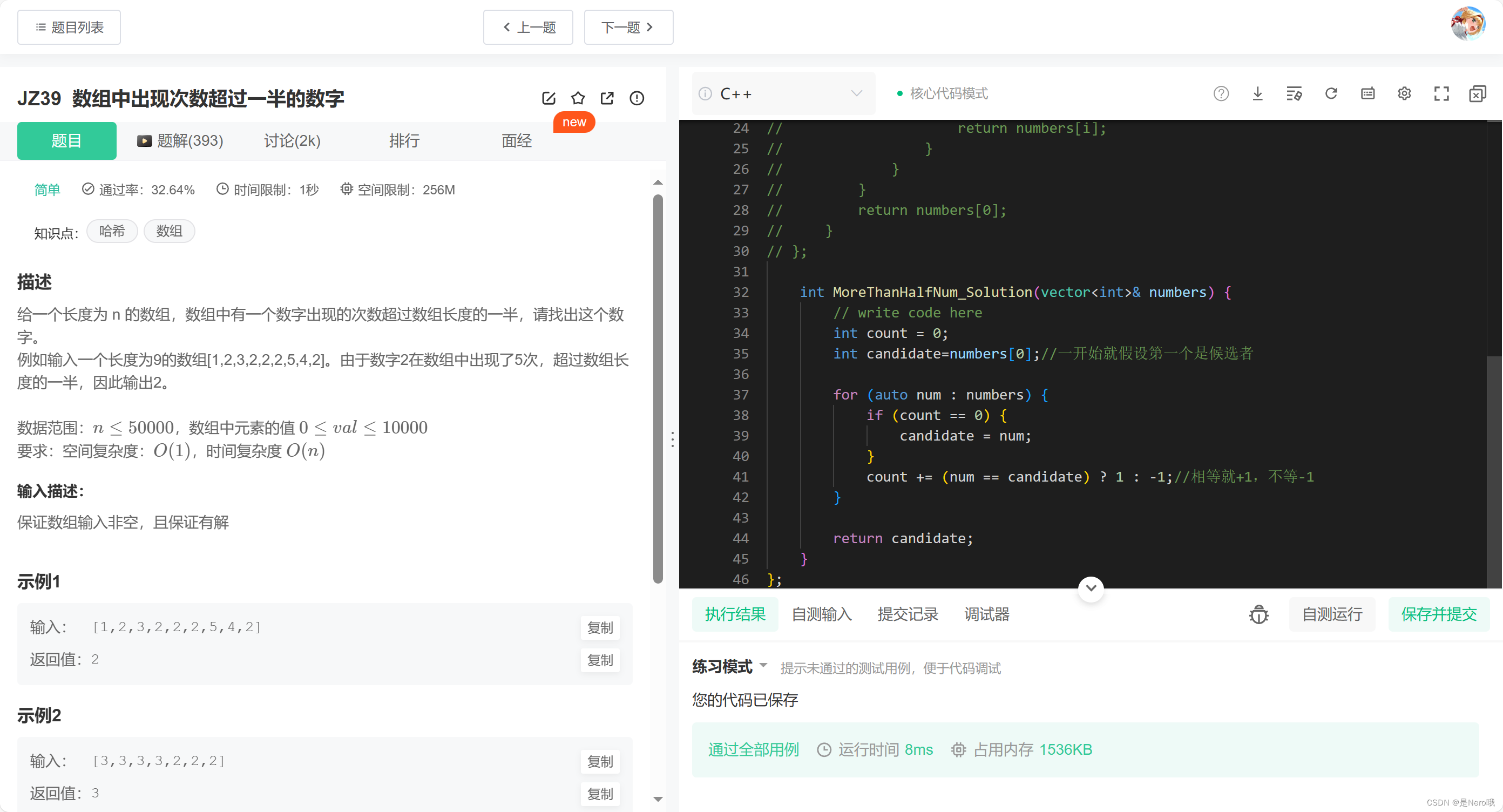
代码2(Boyer-Moore 投票算法)
int MoreThanHalfNum_Solution(vector<int>& numbers) {// write code hereint count = 0;int candidate=numbers[0];//一开始就假设第一个是候选者for (auto num : numbers) {if (count == 0) {candidate = num;}count += (num == candidate) ? 1 : -1;//相等就+1,不等-1}return candidate;}
};
思路2
摩尔投票法的核心思想是抵消。在遍历数组时,我们维护一个候选元素和一个计数器。遍历过程中,如果计数器为0,就将当前元素设为候选元素;如果遇到与候选元素相同的元素,则计数器加1,否则计数器减1。这样做的原因是,如果某个元素出现的次数超过数组长度的一半,那么它与其他元素出现次数的抵消会导致最终留下的候选元素就是出现次数超过一半的元素。
让我们通过一个例子来说明这个过程:
假设数组为:[3, 3, 4, 2, 4, 4, 2, 4, 4]。
我们用变量candidate来存储候选元素,用变量count来存储候选元素的计数器。
- 我们从数组的第一个元素开始,即3。此时候选元素为3,计数器为1。
- 继续遍历数组,遇到的下一个元素还是3。此时计数器变为2。
- 继续遍历数组,遇到的下一个元素是4。此时计数器变为1。
- 继续遍历数组,遇到的下一个元素是2。此时计数器变为0。
- 继续遍历数组,遇到的下一个元素是4。此时候选元素变为4,计数器变为1。
- 继续遍历数组,遇到的下一个元素是4。此时计数器变为2。
- 继续遍历数组,遇到的下一个元素是2。此时计数器变为1。
- 继续遍历数组,遇到的下一个元素是4。此时计数器变为2。
- 继续遍历数组,遇到的下一个元素是4。此时计数器变为3。
最终留下的候选元素是4,它出现的次数超过了数组长度的一半。
这就是摩尔投票法的原理:通过抵消的过程,最终留下的候选元素就是出现次数超过一半的元素。
今天就到这里啦!