文章目录
- 前言
- 参考目录
- 学习笔记
- 0:概述
- 1:一维范围搜索(1d range search)
- 1.1:一维范围搜索实现
- 1.2:一维范围计数:BST 实现
- 1.3:一维范围查找:BST 实现
- 2:线段交点查询(line segment intersection)
- 2.1:线段相交检测:扫描线算法
- 2.2:扫描线算法分析
- 3:Kd树(k-d trees)
- 3.1:二维相交范围查找
- 3.2:二维相交范围查找:网格化实现
- 3.3:网格化实现分析
- 3.4:聚类
- 3.5:空间划分树
- 3.5.1:2d 树构造
- 3.5.2:2d 树实现
- 3.5.3:2d 树 demo:范围搜索
- 3.5.4:2d 树范围搜索分析
- 3.5.5:2d 树 demo:最近邻搜索
- 3.5.6:2d 树最近邻搜索分析
- 3.6:群集行为模拟(Boids)
- 3.7:Kd 树
- 3.8:N体模拟(物理学经典问题)
前言
本篇内容属于《算法》视频的番外篇,是关于前面几篇所学内容 BST 的扩展应用,因此在学习本篇之前,请先学习或回顾一下前面几篇的内容:《3.1 符号表》、《3.2 二叉查找树》、《3.3 平衡查找树》。
温馨提示:如果不知道 BST 是什么的朋友强烈建议先看看前面几个章节的内容。: )
由于本章节的内容很多,所以分成了上下两篇,本篇主要内容包括:一维范围搜索、线段交点查询、Kd树。
参考目录
- B站 普林斯顿大学《Algorithms》视频课
(请自行搜索。主要以该视频课顺序来进行笔记整理,课程讲述的教授本人是该书原版作者之一 Robert Sedgewick。) - 微信读书《算法(第4版)》
- 官方网站
学习笔记
注1:所有 demo 演示均为视频 PPT demo 截图。
注2:如果 PPT 截图中没有翻译,会在下面进行汉化翻译,因为内容比较多,本文不再一一说明。
0:概述
本章节主要介绍以下内容:
- 一维范围搜索(
1d range search):在一维空间中查找给定范围内符合条件的元素。 - 线段交点查询(
line segment intersection):确定一组线段之间是否存在相交情况,并找出所有交点。 - Kd树(
k-d trees,d代表维度):一种用于高效检索多维数据(如二维、三维空间中的点或更高维度)的数据结构,常用于诸如最近邻搜索、空间分割等几何应用。 - 区间搜索树(
interval search trees):一种特殊的数据结构,用来存储和快速查询区间信息,比如找到与给定区间有重叠的所有区间。 - 矩形交集问题(
rectangle intersection):处理多个矩形区域之间的交集检测,在图形学、GIS等领域广泛应用。
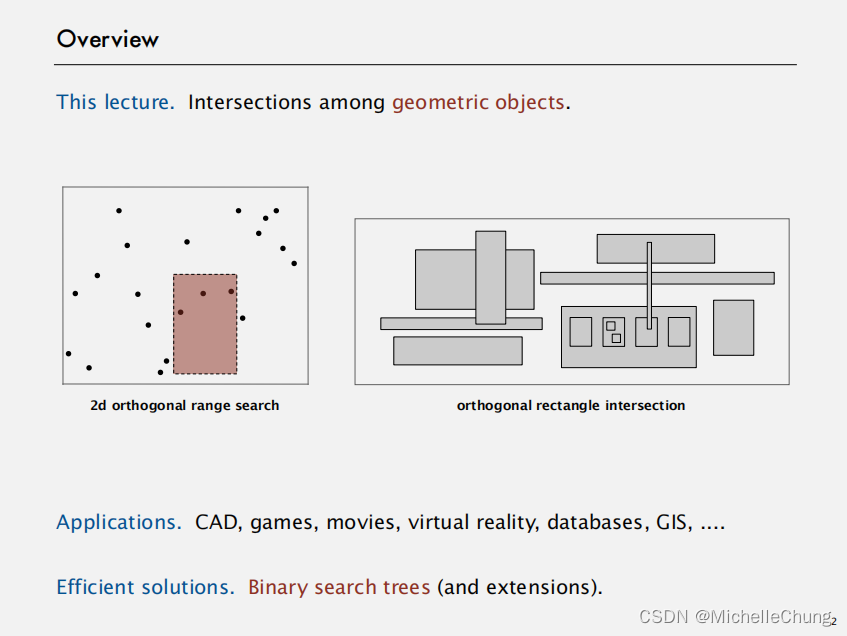
本课程:几何对象间的交集运算。
应用:CAD(计算机辅助设计)、游戏开发、电影制作、虚拟现实技术(VR)以及数据库管理等领域……
有效解决方案:BST(及其扩展)。
1:一维范围搜索(1d range search)
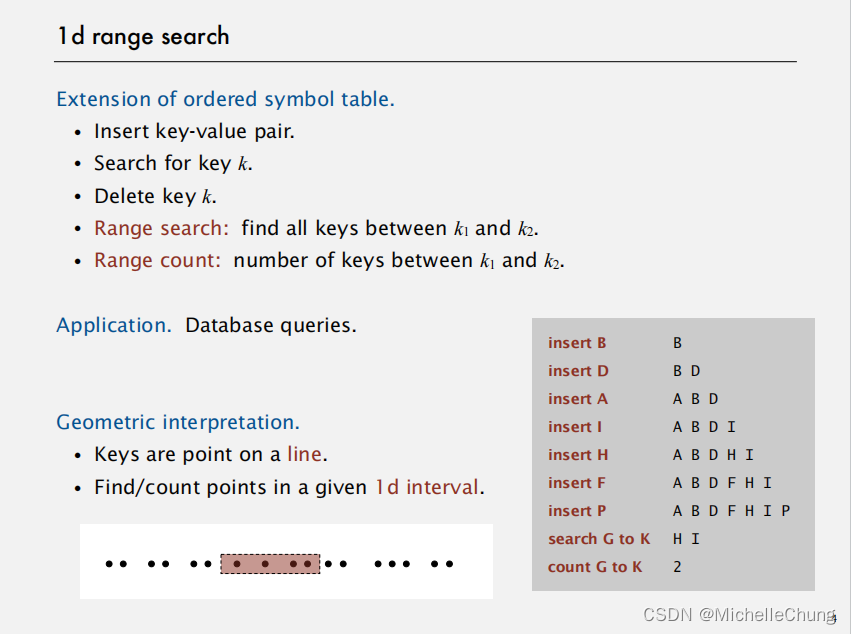
有序符号表的扩展功能:
- 插入键值对。
- 搜索给定键 k。
- 删除键 k。
- 范围搜索:找出所有介于 k1 和 k2 之间的键。
- 范围计数:统计在 k1 和 k2 之间键的数量。
应用场景:数据库查询操作。
进一步具体解释:
一维范围搜索是一种针对一维数据结构(例如有序数组或增强型二叉搜索树)的操作,它允许不仅查找单个键值,还能高效地找出特定范围内所有符合条件的键。此类功能广泛应用于数据库查询领域,例如快速检索满足特定条件的一系列记录。
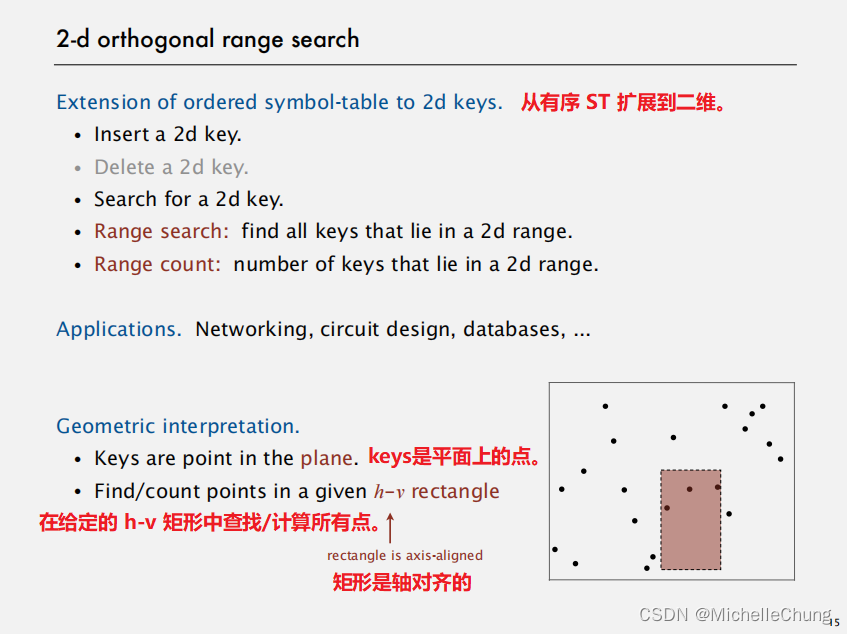
几何解释:
- 键是直线上的点。
- 在给定的一维区间内查找/计算点的数量。
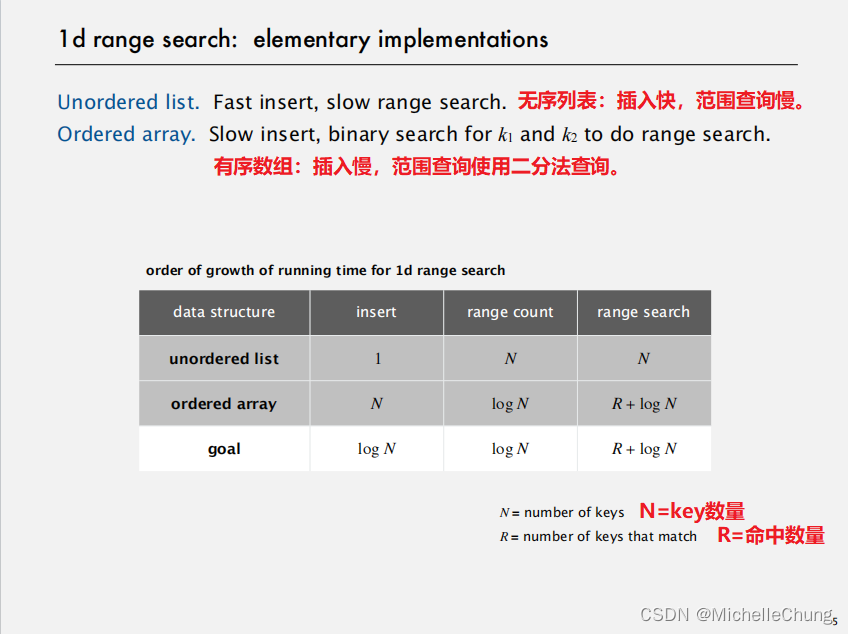
1.1:一维范围搜索实现
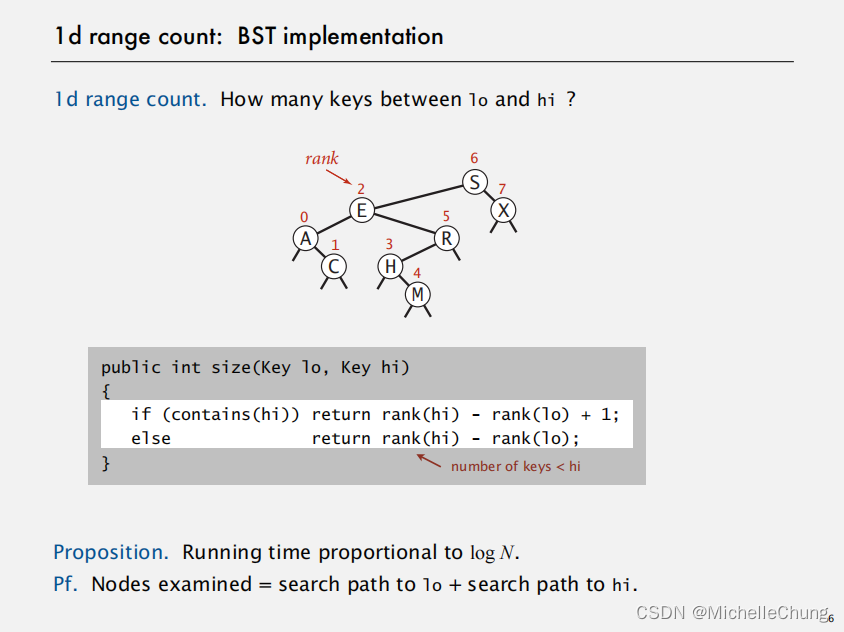
1.2:一维范围计数:BST 实现
命题:运行时间与 log N 成正比。
证明:搜索过程中检查的节点数量等于从根节点到 lo 节点的搜索路径长度加上从根节点到 hi 节点的搜索路径长度。
edu.princeton.cs.algs4.BST#size
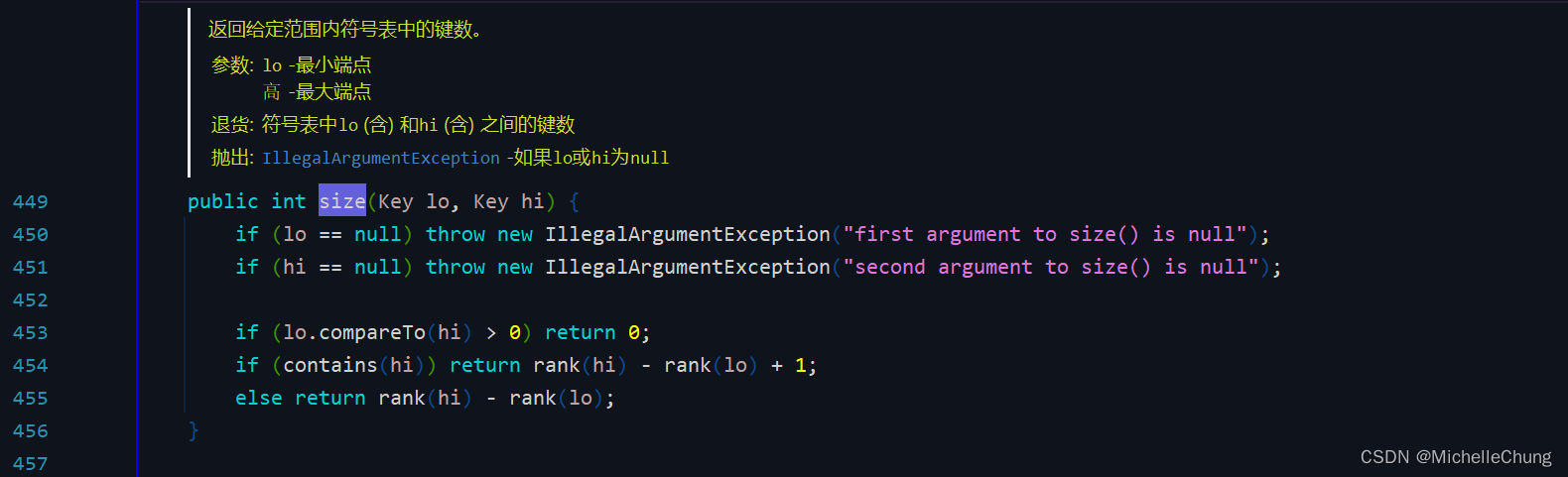
1.3:一维范围查找:BST 实现
一维范围搜索:寻找所有在 lo 和 hi 之间的键值。
(递归步骤如下:)
- 在左子树(如果有可能落入指定范围内的键值)中查找所有键值。
- 检查当前节点中的键值是否位于指定范围内。
- 若右子树中可能存在落在指定范围内的键值,则继续递归地在右子树中查找所有键值。
命题:运行时间与 R + log N 成正比。
证明:搜索过程中检查的节点数量等于,从根节点到 lo 节点的搜索路径长度,加上从根节点到 hi 节点的搜索路径长度,再加上在指定范围(lo 和 hi 之间)内匹配到的键值个数(即 R)。
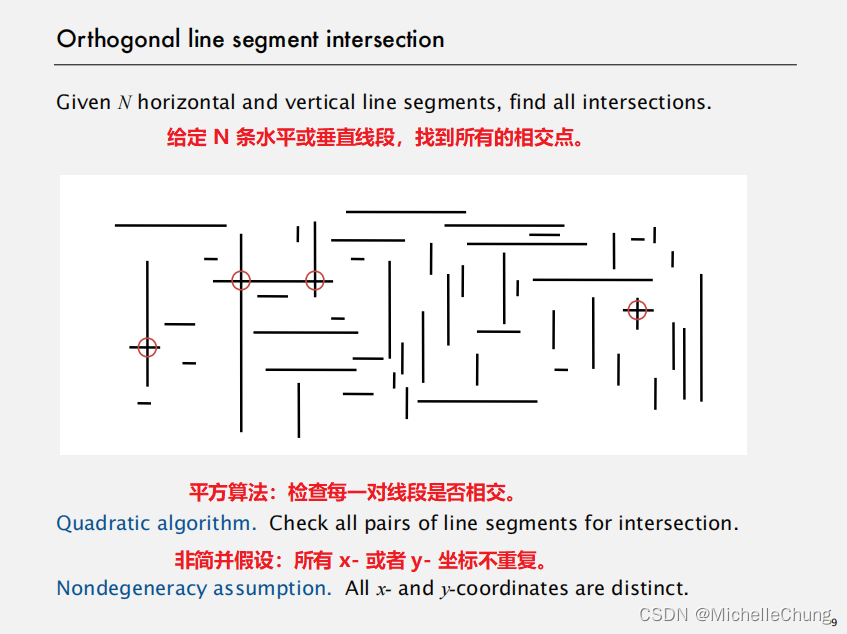
2:线段交点查询(line segment intersection)
注:平方算法,指的是平方时间复杂度,在这里也是指最简单的暴力算法(自然算法)。
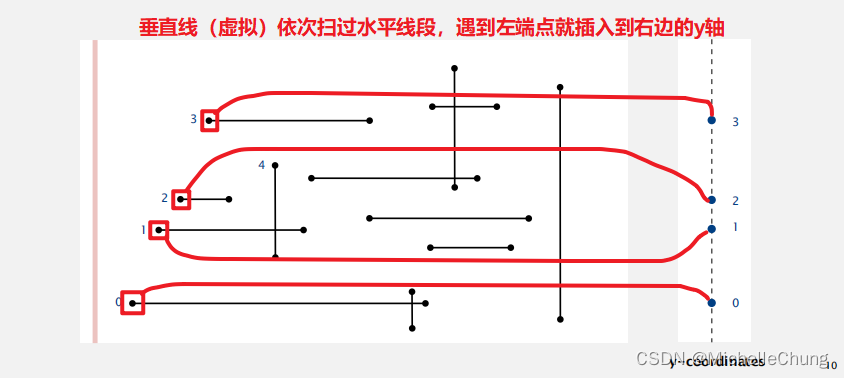
2.1:线段相交检测:扫描线算法
从左到右扫过一条垂直线。
- x 坐标定义事件。
- 对于水平线段(左端点):将 y 坐标插入到 BST 中。
该算法步骤解释如下:
- 使用一种从左至右的扫描线方法,在水平方向上移动一条虚拟的垂直线。
- 当垂直扫描线与每个线段的左端点相交时,这个相交位置对应的 x 坐标被视为一个“事件”。
- 对于每一个 h 纵向线段(即沿 y 轴方向延伸的线段),当其左端点与扫描线相交时,将该线段左端点的 y 坐标作为一个关键值插入到二叉搜索树(BST)中。通过 BST 可以方便地管理和查询与当前扫描线相交的所有线段信息,进而判断是否存在线段间的交叉情况。
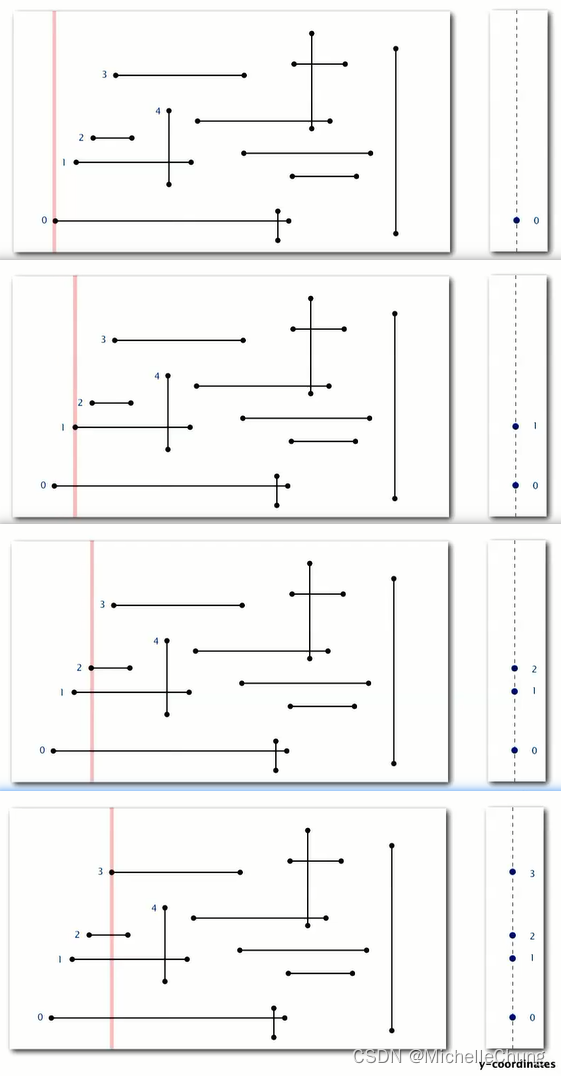
移动过程:
从左到右扫过一条垂直线。
- x 坐标定义事件。
- 对于水平线段(左端点):将 y 坐标插入到 BST 中。
- 对于水平线段(右端点):将 y 坐标从 BST 中移除。
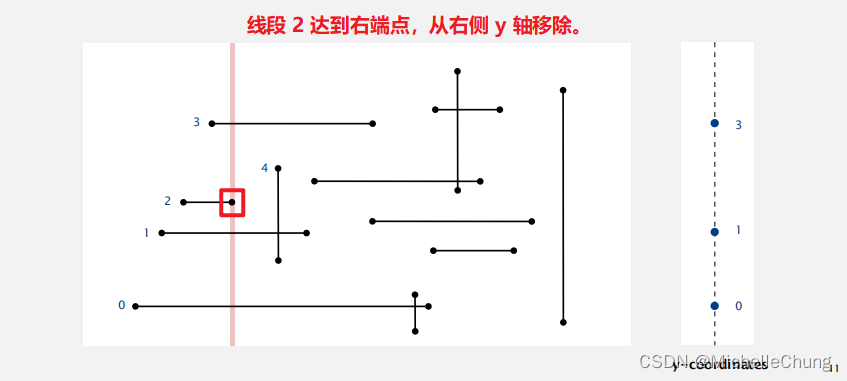
整个线段 2 已经扫描处理完毕,没有相交点。
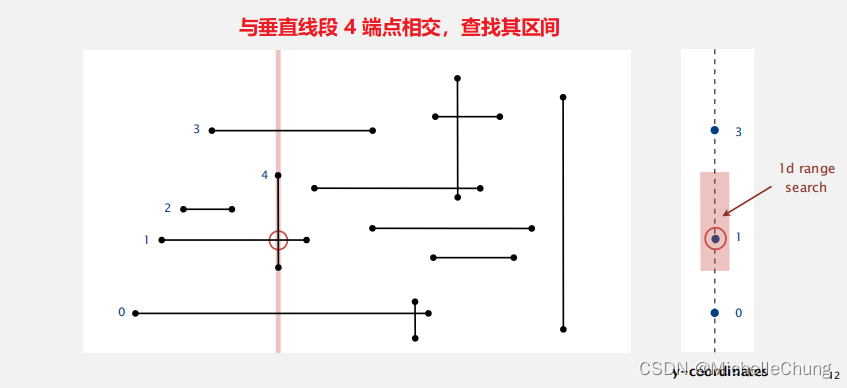
从左到右扫过一条垂直线。
- x 坐标定义事件。
- 对于水平线段(左端点):将 y 坐标插入到 BST 中。
- 对于水平线段(右端点):将 y 坐标从 BST 中移除。
- 对于垂直线段:对y-端点区间进行范围搜索。
2.2:扫描线算法分析
命题:使用扫描线算法在 N 条正交线段中找出所有 R 个相交点所需的时间与 N log N + R 成正比。
证明:
- 首先,将所有 x 坐标放入一个优先队列(或进行排序)。(N log N)
- 当遇到 h 纵向线段时,将其 y 坐标插入到二叉搜索树(BST)中。(N log N)
- 遇到 h 纵向线段的右端点时,从 BST 中删除对应的 y 坐标。(N log N)
- 对于 v 横向线段,利用 BST 进行范围搜索以查找可能存在的相交情况。(N log N + R)
总结:扫描线算法能够将二维正交线段相交搜索问题转换为一维范围搜索问题,从而有效地降低问题复杂度。
3:Kd树(k-d trees)
Now we’re going to look at k-d trees, which is an extension of BSTs that allow us to do efficient processing of sets of points in space. And it’s very flexible and very useful in lots of applications.
Kd树,它是 BST 的扩展,使我们能够有效地处理空间中的点集。它非常灵活,在许多应用中非常有用。
3.1:二维相交范围查找
3.2:二维相交范围查找:网格化实现
网格化实现方法:
- 将空间划分为 M x M 的网格,每个单元格是一个正方形区域。
- 对于每个网格正方形,构建一个存储其内部点坐标的列表数据结构。
- 利用一个二维数组(矩阵)来快速定位到相应正方形及其包含的点集合。
- 插入操作:将坐标 (x, y) 添加到对应正方形的点列表中。
- 范围搜索:仅遍历并检查与指定二维查询范围相交的那些网格正方形,然后在其包含的点列表中查找符合条件的点。
3.3:网格化实现分析
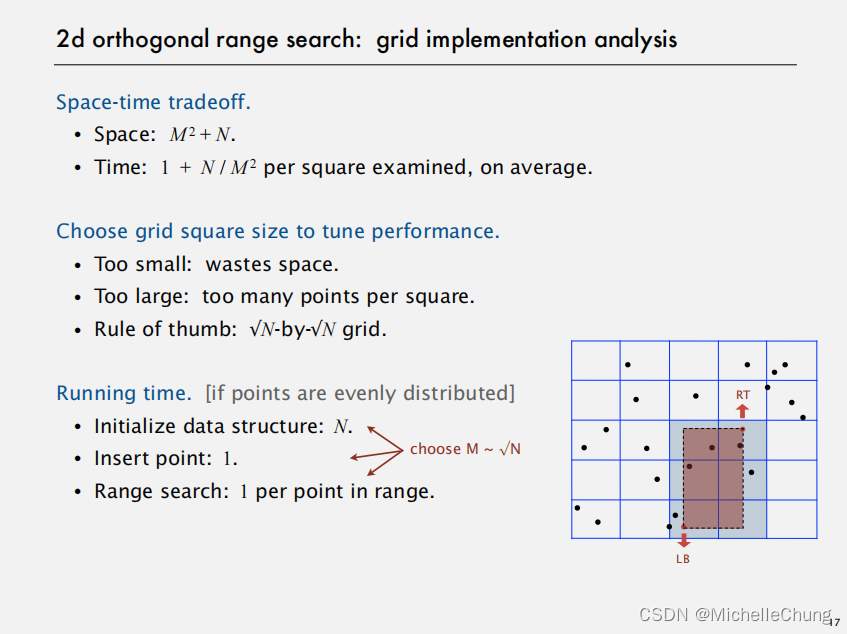
空间-时间权衡:
- 空间:M^2 + N。
- 时间:对于每个被检查的正方形,平均时间为 1 + N/M^2。
为了调整性能,选择合适的网格正方形尺寸:
- 太小:则会浪费存储空间。
- 太大:则每个正方形内包含的点数过多(影响搜索效率)。
- 经验法则:通常选择一个约 √N-by-√N 的网格大小。
运行时间(假设点均匀分布):
- 初始化数据结构:O(N)
- 插入一个点:O(1)
- 范围搜索:对于范围内的每个点,平均需要 O(1)。因此,若范围内的点数量为 K,则范围搜索总时间为 O(K)。
(建议选取 M 的值大约为 √N,以优化空间和时间之间的平衡。)
3.4:聚类
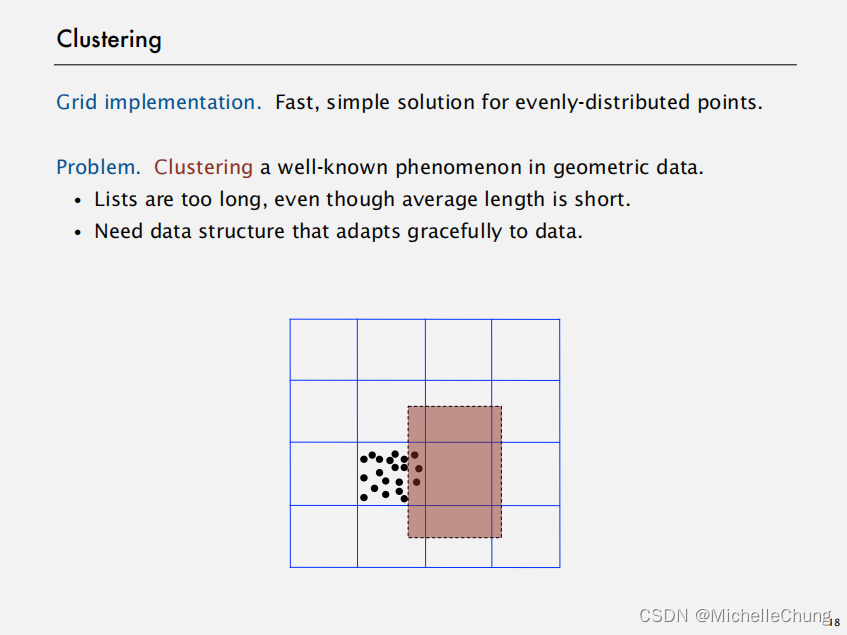
网格化实现:对于均匀分布的点提供快速、简单的解决方案。
问题描述:在处理几何数据时,聚类是一种普遍存在的现象。
- 即使平均长度较短,列表也可能过长。
- 需要一种能够平滑适应实际数据分布特点的数据结构。
3.5:空间划分树
使用树递归划分二维空间。
- Grid(网格): 将二维空间均匀地划分为多个正方形区域。
使用网格将2D空间均匀分割成多个正方形分区。 - 2d tree(二叉空间划分树的简化形式): 递归地将二维空间分割成两个半平面。
通过递归方法将2D空间划分为两个互斥的半空间子区域。 - Quadtree(四叉树): 递归地将空间分割成四个象限。
采用递归方式将二维空间分割成四个相等或大致相等的区域,每个区域代表原来空间的一个象限。 - BSP tree(二叉空间分割树,Binary Space Partitioning Tree): 递归地将空间分割为两个不相交的区域。
通过递归算法将2D空间不断分割成两个非重叠的部分,并构建二叉树结构来表示这一过程。在BSP树中,每次分割都是通过一个分割面(通常是一个直线或者超平面)来实现的,这个面将整个空间一分为二。
3.5.1:2d 树构造
递归地将二维空间分割成两个(半平面)。
利用点以及点所在的水平线或是垂直线分割。
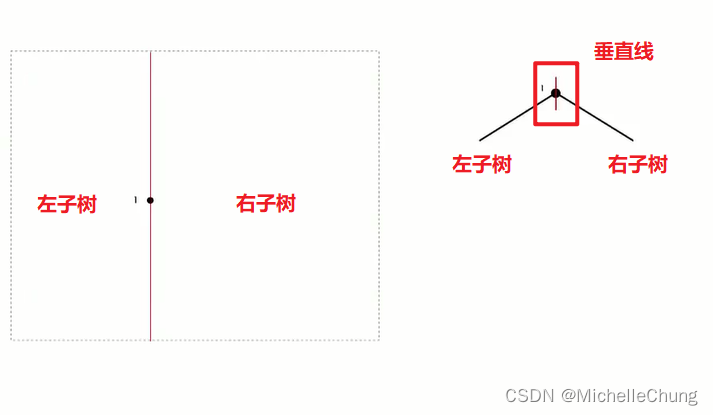
第一个点(任意点,垂直线分割):
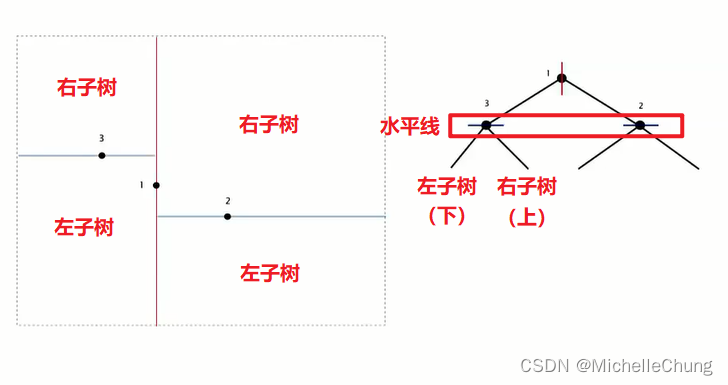
第二个点、第三个点(水平线分割):
- 垂直线与水平线交替分割
- 垂直线左右分别代表左子树、右子树
- 水平线下上分别代表左子树、右子树
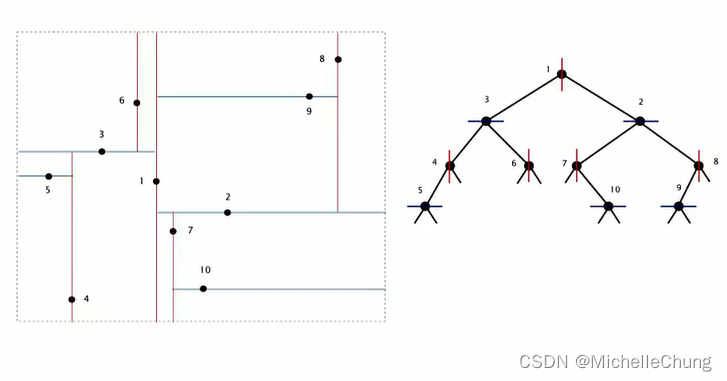
最终得到的树:
(建议按照节点顺序捋一遍划分结果)
3.5.2:2d 树实现
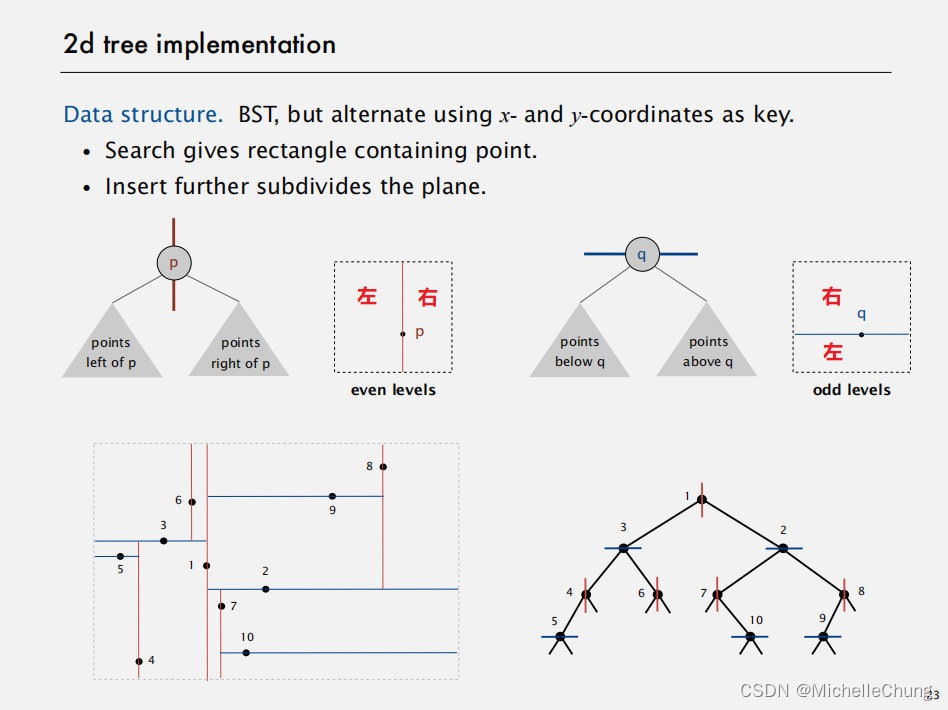
数据结构:基于 BST 的一种变体,但交替使用x坐标和y坐标作为键值。
-
搜索操作:能够找到包含指定点的矩形区域。
即,给定一个二维空间中的点,该数据结构能够快速找到包含这个点的最小或特定大小的矩形区域。 -
插入操作:进一步细分平面。
这意味着每当你向这个数据结构中插入一个新的点时,会根据点的坐标自动进行空间划分,可能需要对现有的树结构进行调整以适应新的分割需求。
3.5.3:2d 树 demo:范围搜索
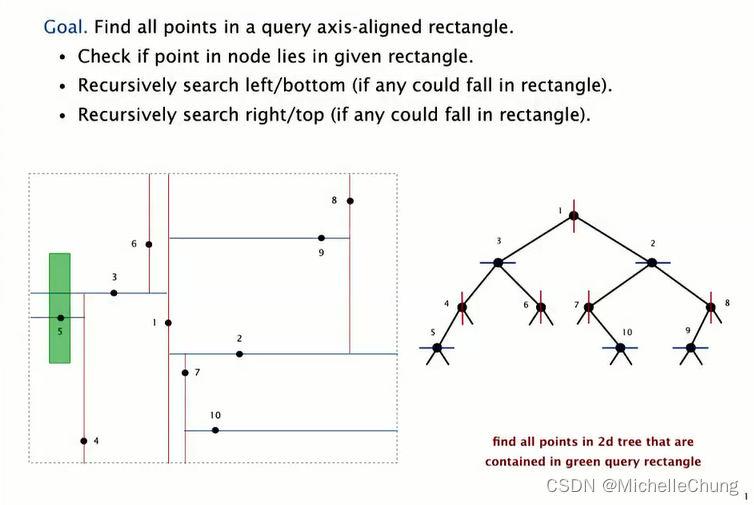
目标:在查询指定的轴对齐矩形内查找所有点。(绿色矩形内的所有点)
步骤:
- 检查节点中的点是否位于给定的矩形内。
(首先,判断当前数据结构节点中存储的点是否落在所查询的轴对齐矩形区域内。) - 递归搜索左/下子树(如果有任何点可能落入矩形内)。
(若当前节点的左子树或下子树(在某些空间划分树如四叉树中为下子树,在二叉空间分割树中可能理解为y坐标较小的子树)所代表的空间区域与查询矩形有交集,则进一步深入这些子树进行递归搜索。) - 递归搜索右/上子树(如果有任何点可能落入矩形内)。
(同样地,若当前节点的右子树或上子树(在某些空间划分树中为上子树,在二叉空间分割树中可能理解为y坐标较大的子树)所代表的空间区域与查询矩形有交集,则继续深入这些子树进行递归搜索。)
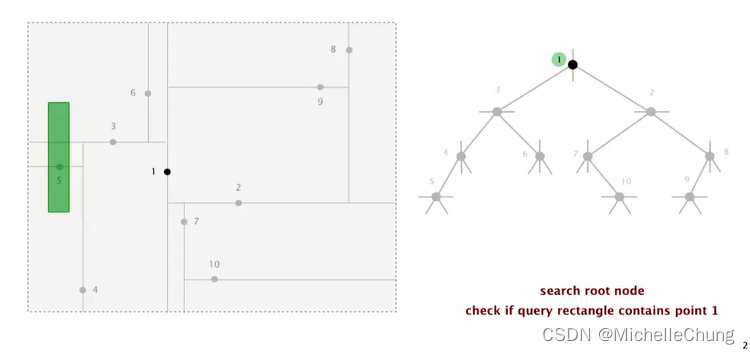
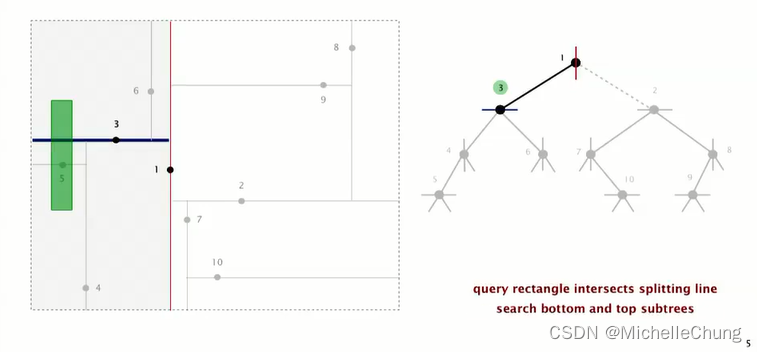
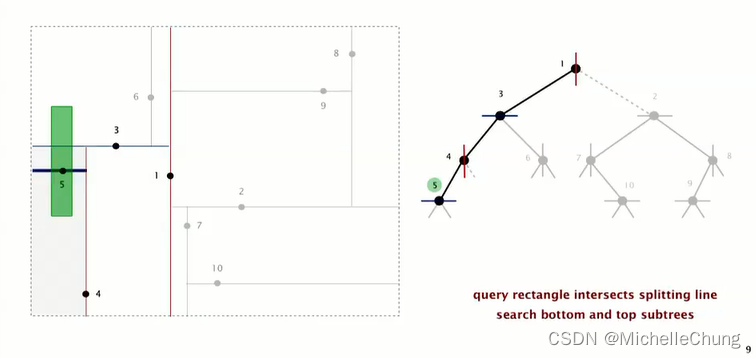
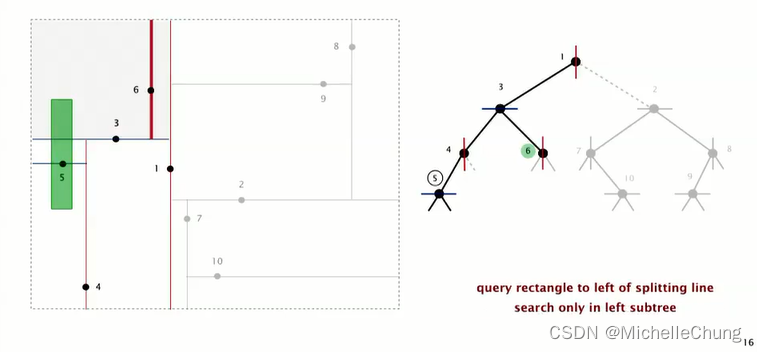
检查矩形是否包含根节点 1:
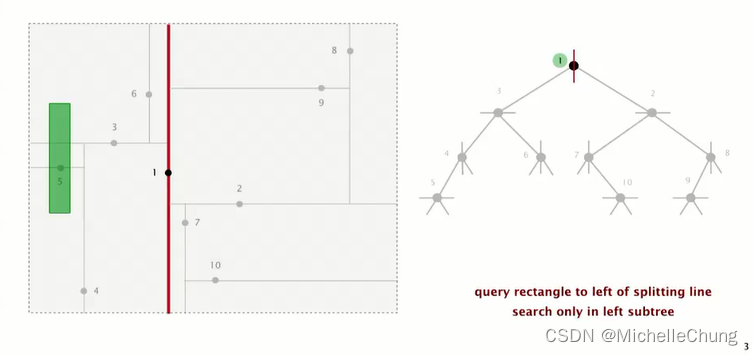
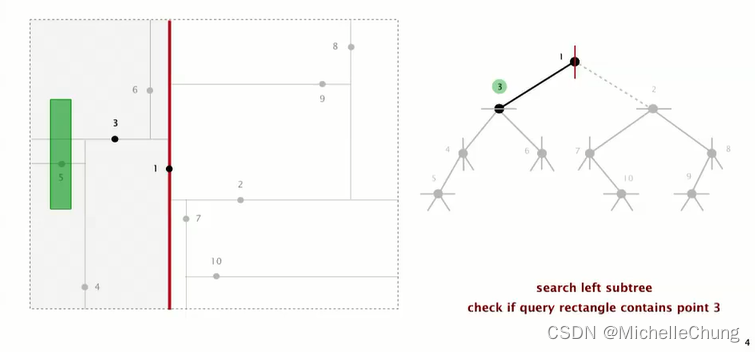
没有包含根节点 1,在根节点 1 左侧,继续搜索根节点 1 左子树节点 3:
没有包含节点 3,但 矩形与节点 3 所在的水平线相交,因此节点 3 左右子树都需要进行搜索:
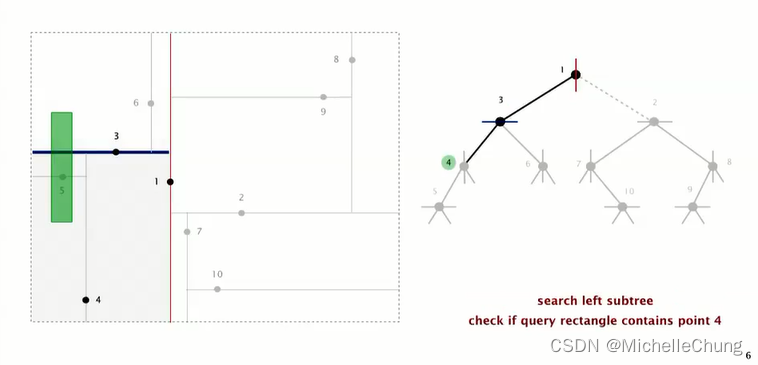
搜索节点 3 左子树节点 4:
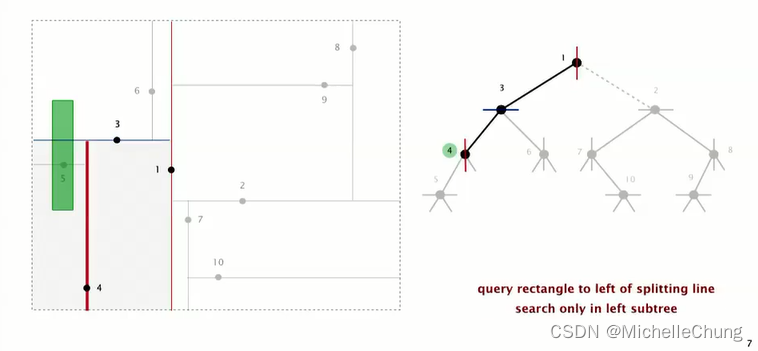
矩形没有包含节点 4,在节点 4 左侧,需要搜索节点 4 左子树节点 5:
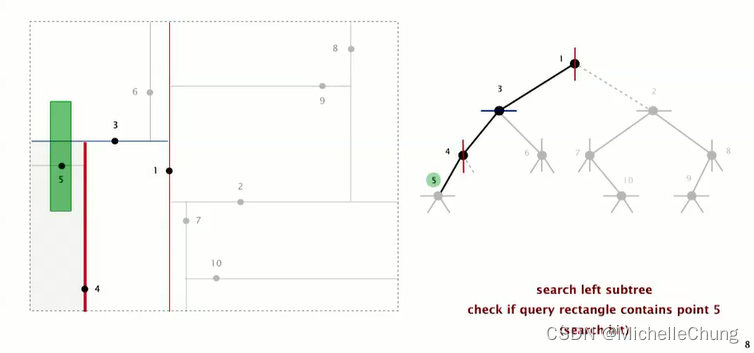
矩形包含节点 4 左子树节点 5,搜索命中:
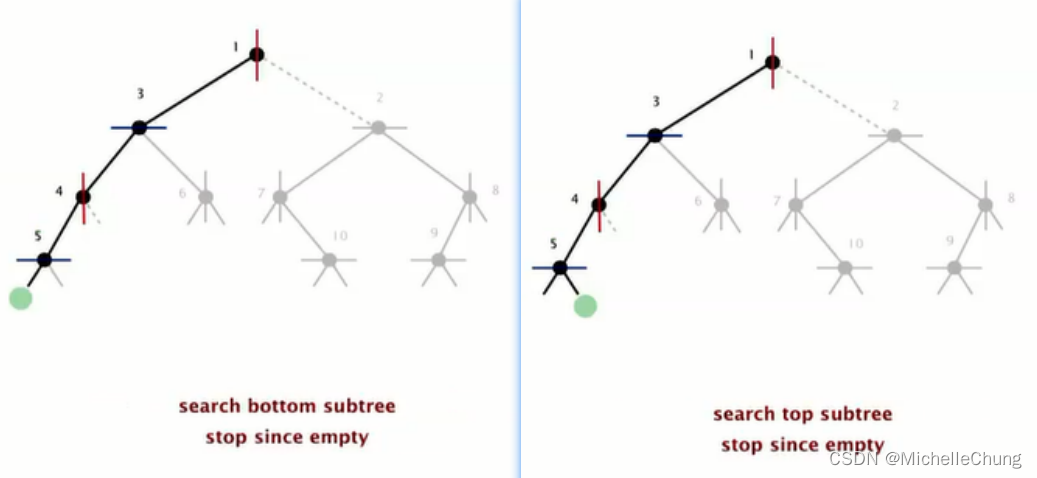
矩形与节点 5 所在的水平线相交,因此也要搜索节点 5 左右子树:
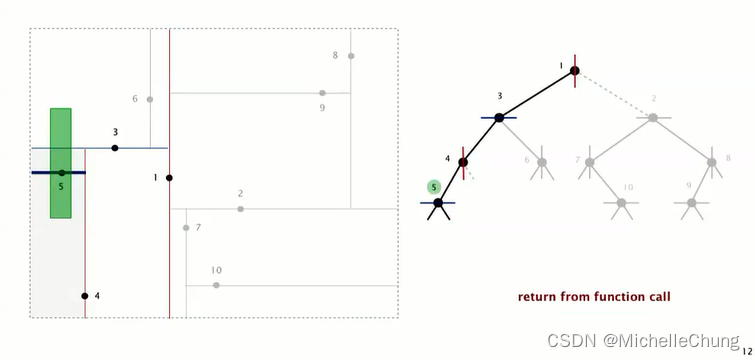
节点 5 左右子树(水平线上下两侧)都为空,完成节点 3 左子树搜索:
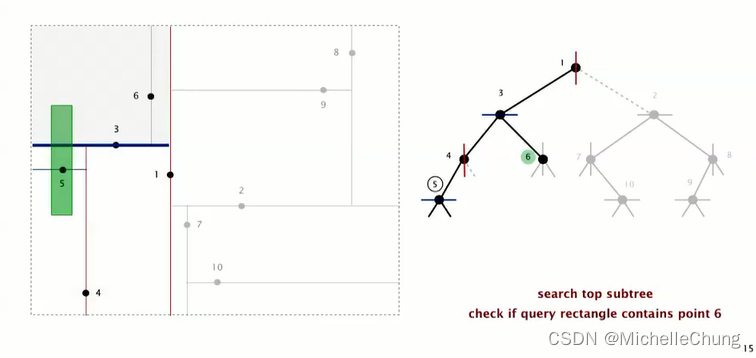
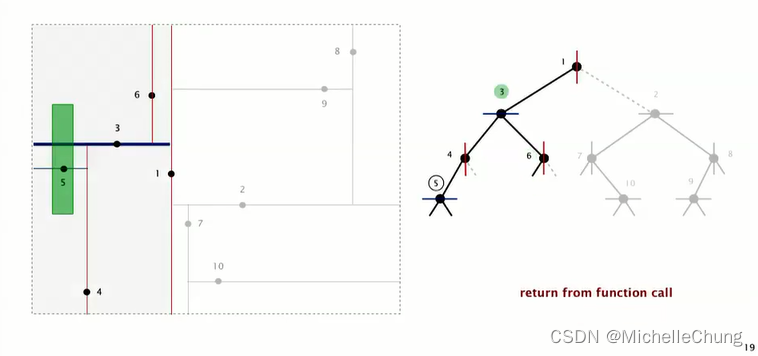
继续搜索节点 3 右子树节点 6:
矩形没有包含节点 6,在节点 6 左侧,需要搜索节点 6 左子树:
节点 6 左子树为空,完成节点 3 右子树搜索:
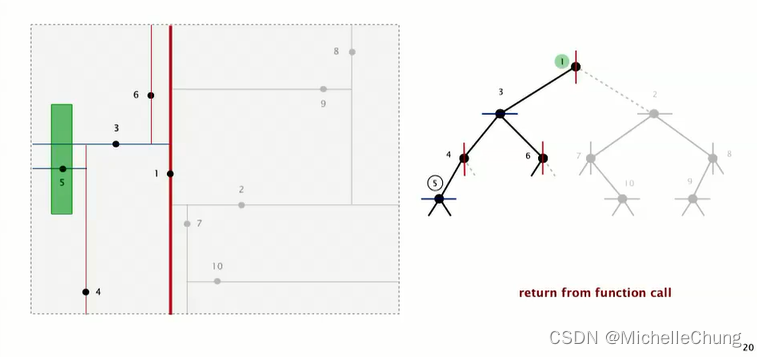
完成根节点 1 左子树搜索:
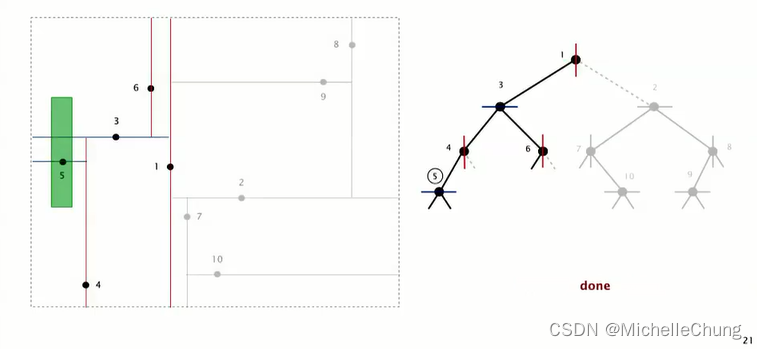
完成所有搜索:
3.5.4:2d 树范围搜索分析
典型案例:R + log N
最坏的情况(假设树是平衡的):R + √N
Prof. Sedgewick:2D 树分析有点超出我们的范围,但对于很多实际应用来说,它易于实现且值得使用。
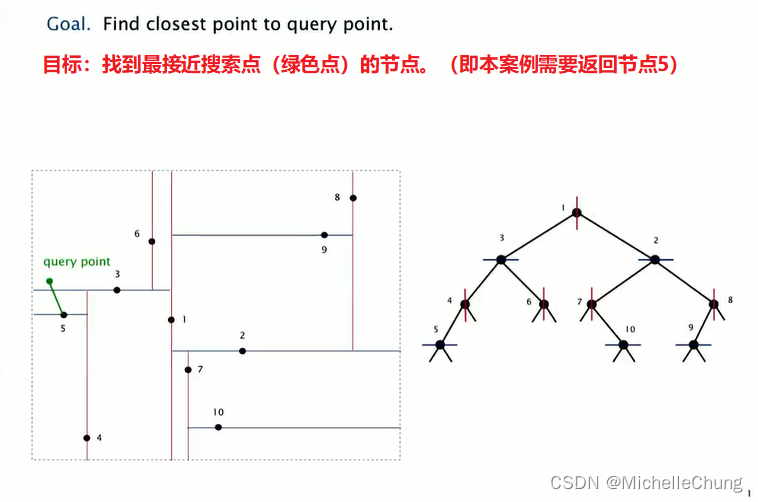
3.5.5:2d 树 demo:最近邻搜索
步骤:
- 检查节点中的点到查询点的距离。
(首先计算当前数据结构节点中存储的点到待查询点之间的距离。) - 递归搜索左/下子树(如果可能包含更近的点)。
(若当前节点的左子树或下子树所代表的空间区域有可能包含离查询点更近的点,则进一步深入这些子树进行递归搜索。) - 递归搜索右/上子树(如果可能包含更近的点)。
(同样地,若当前节点的右子树或上子树所代表的空间区域有可能包含离查询点更近的点,则继续深入这些子树进行递归搜索。) - 组织方法以便从查找查询点开始。
(设计算法时确保优先从最可能包含查询点或离查询点最近的区域开始搜索,以提高搜索效率。)
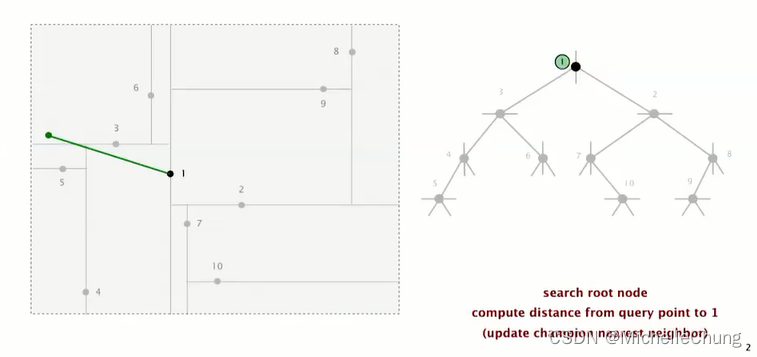
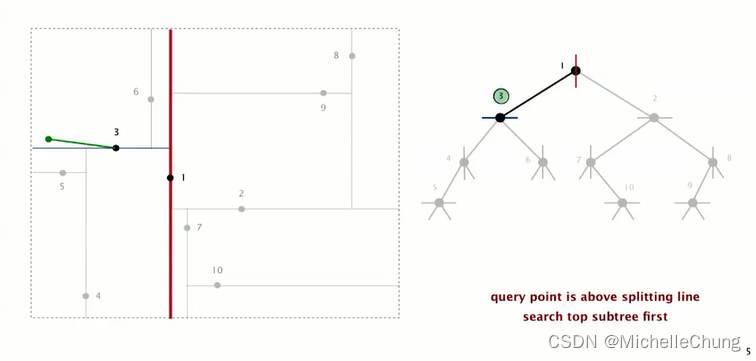
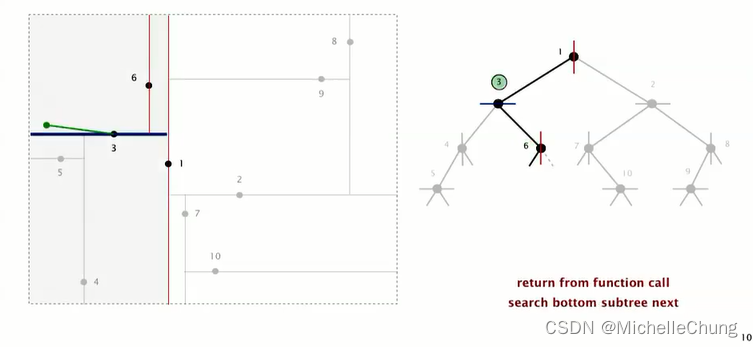
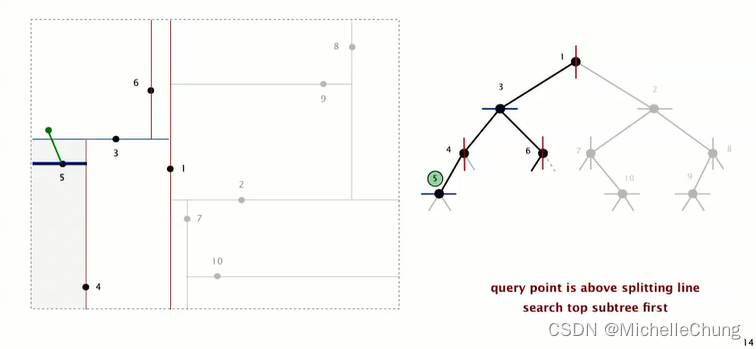
检查根节点 1,计算与查询点的距离,更新最邻近点为 1:
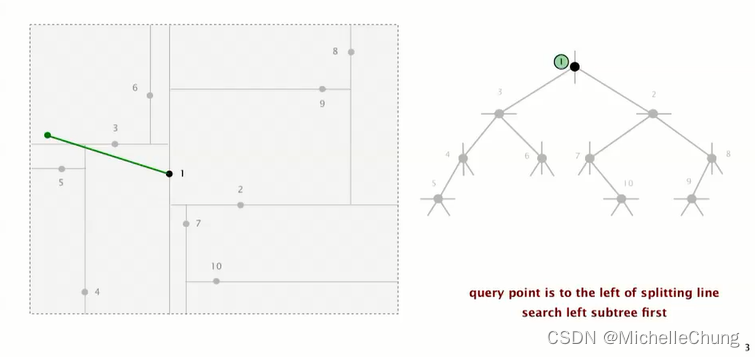
查询点位于根节点 1 分割线左侧,搜索根节点 1 左子树节点 3:
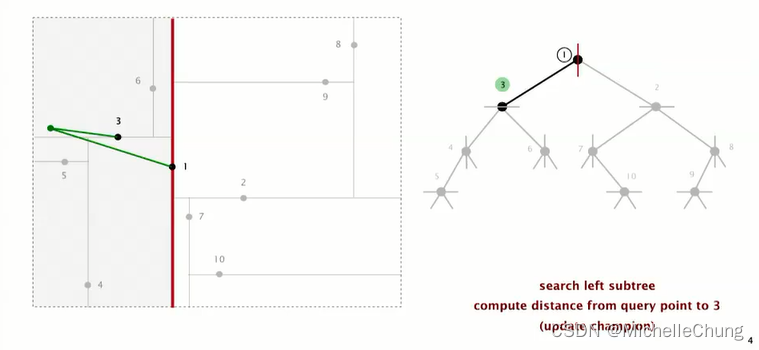
计算节点 3 与查询点距离,两者距离更近,更新最邻近点为 3:
由于节点 3 更接近查询点,因此后续不需要再搜索根节点 1 右子树,因为此时根节点 1 右子树不会有比 3 更接近的点。(注,如果根节点 1 距离更近,则需要继续搜索右子树。)
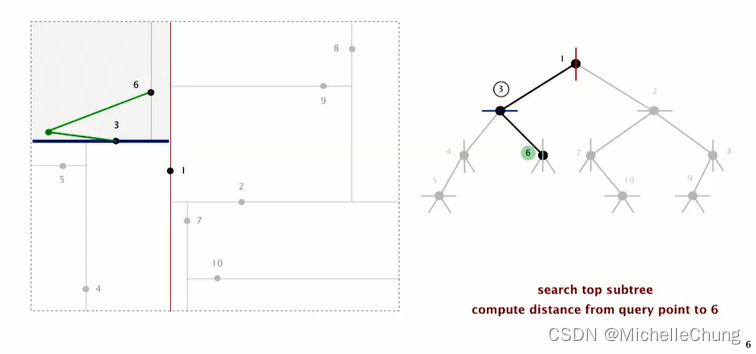
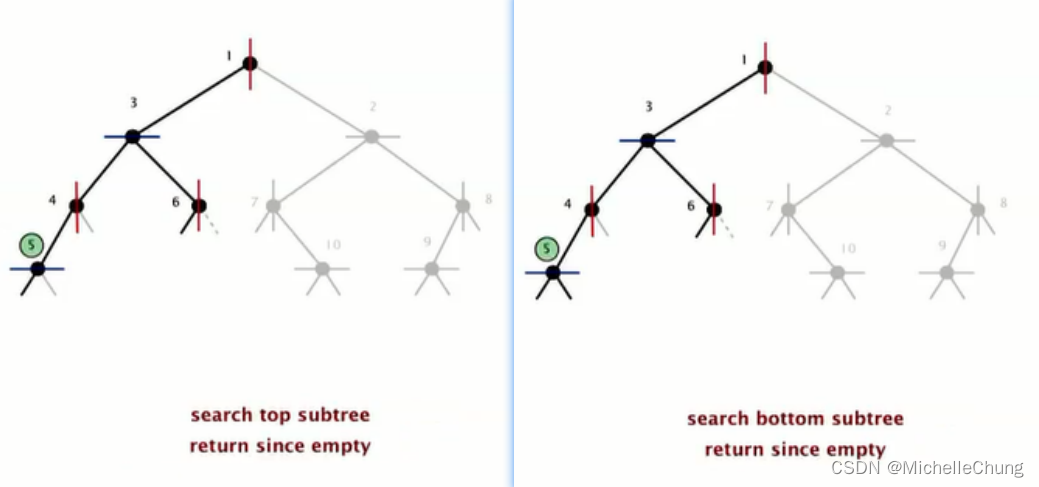
查询点在节点 3 上侧,先搜索节点 3 右子树节点 6:
节点 6 与查询点距离比较大,因此不需要更新最邻近点:
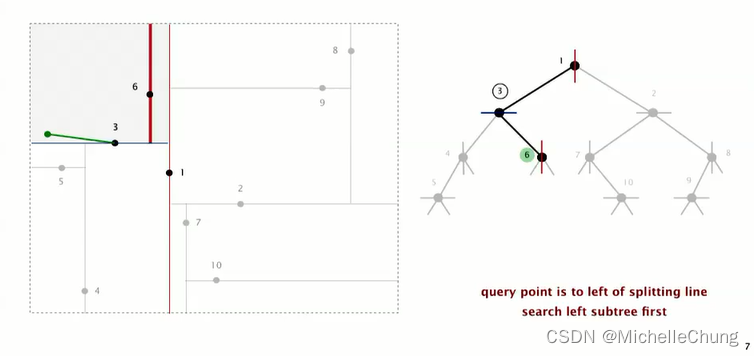
继续搜索节点 6 左子树:
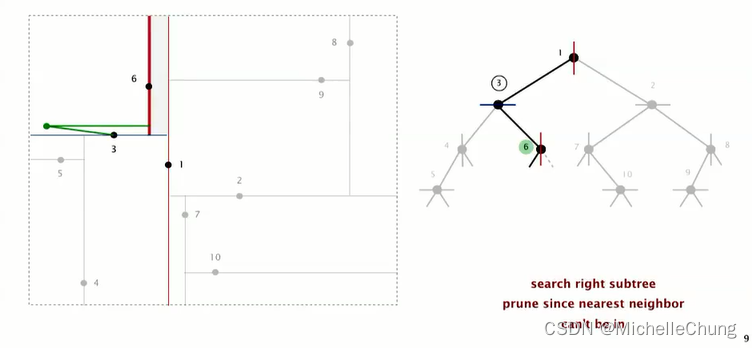
节点 6 左子树为空,不比搜索节点 6 右子树,因为不会有比节点 3 距离更近的点:
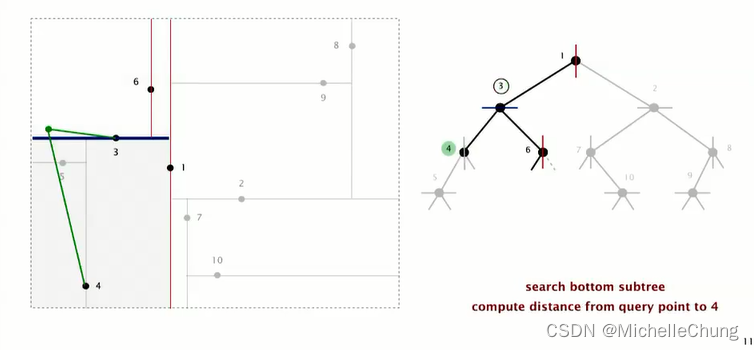
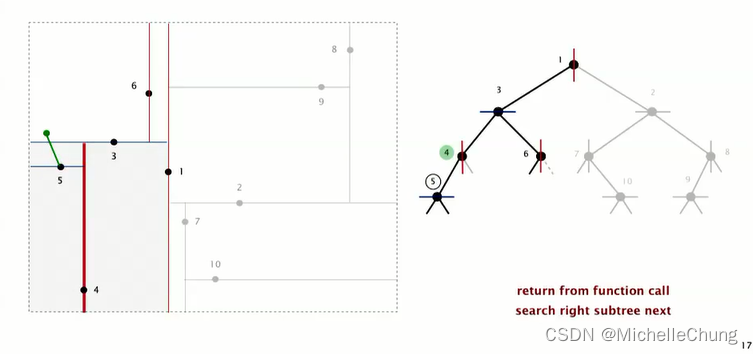
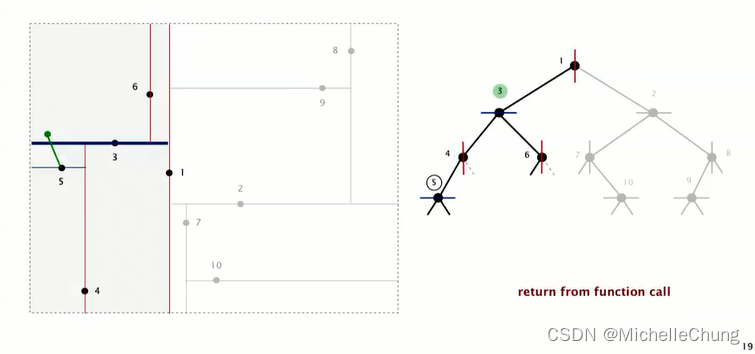
回到节点 3,继续搜索节点 3 下侧(即左子树)节点 4:
节点 4 与查询点距离比较大,因此不需要更新最邻近点:
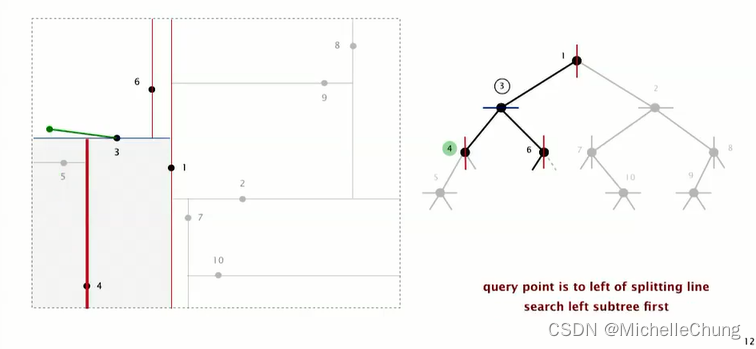
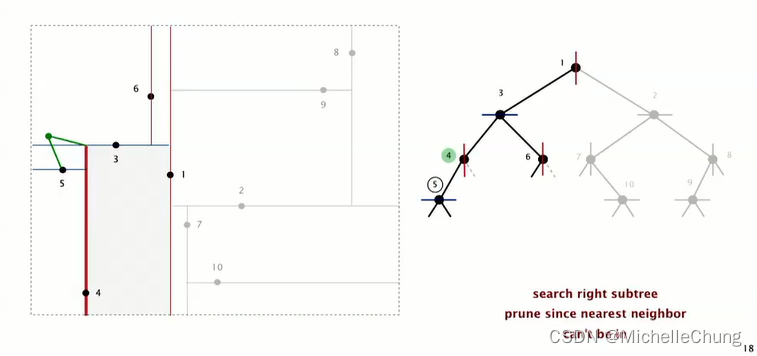
继续搜索节点 4 左子树(查询点在分割线左侧)节点 5:
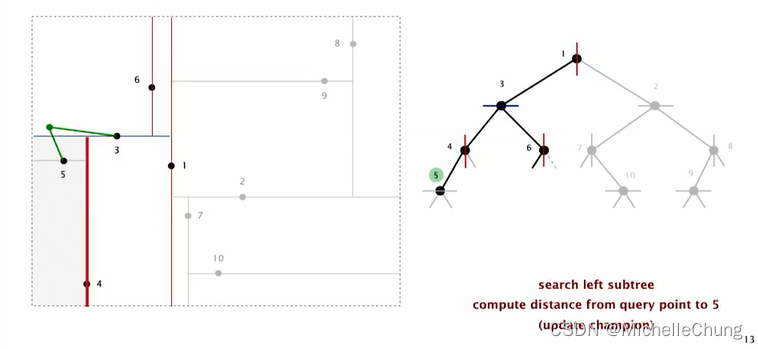
节点 5 与查询点两者距离更近,更新最邻近点为 5:
查询节点 5 左右子树是否有更邻近的点:
节点 5 左右子树(水平线上下两侧)都为空,完成节点 4 左子树搜索:
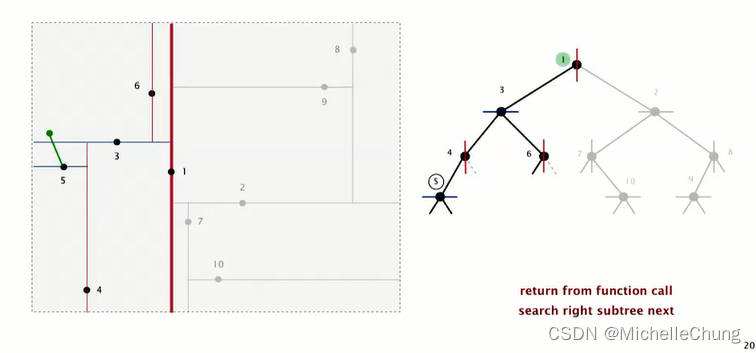
不需要继续搜索节点 4 右子树,因为不会有比节点 5 距离更近的点:
完成节点 3 左子树搜索:
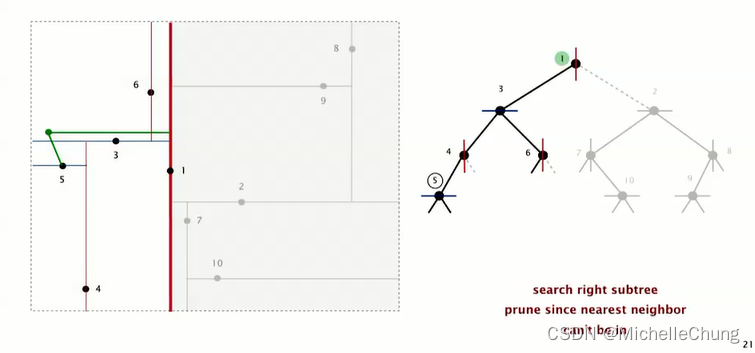
完成根节点 1 左子树搜索:
前面说过,根节点 1 右子树不需要再次搜索:
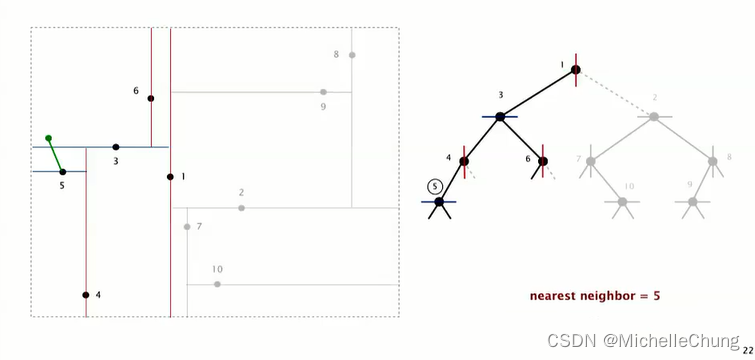
最终结果,最邻近点为节点 5:
3.5.6:2d 树最近邻搜索分析
典型案例:log N
最坏的情况(即使树是平衡的):N
3.6:群集行为模拟(Boids)
Boids(群集行为模拟)。三个简单规则形成的复杂的群体行为:
- 避碰规则(Collision Avoidance):计算当前个体与最近的k个邻近个体之间的距离和方向,并根据这些信息调整自身运动以远离最近的k个boid。
- 群体中心趋向规则(Flock Centering):将运动方向调整至最近的k个boid质心的方向。
- 速度匹配规则(Velocity Matching):将当前个体的速度调整为最近的k个boid速度的平均值。
看不懂的话没关系,我又去找了一下 关于这个算法的介绍:
Boid:
三个基本原则:
3.7:Kd 树
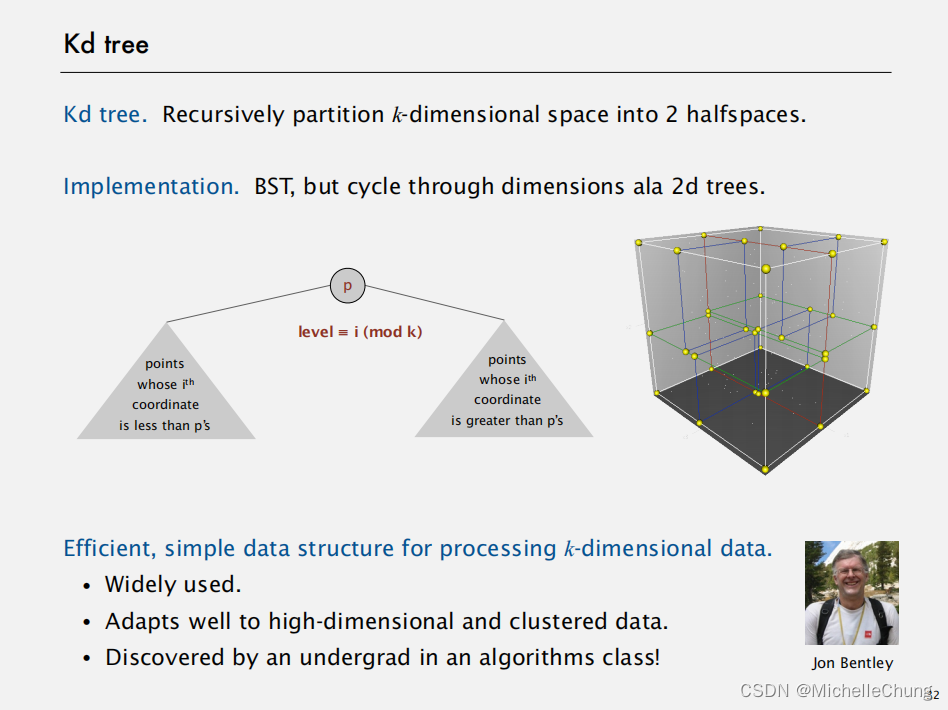
Kd树:递归地将 k 维空间划分为两个(半空间)。
实现方式:BST,使用类似于2d树的维度循环方法。
具体解释:
这里的实现是指,在设计数据结构时,虽然基础结构是BST,但在处理多维数据(如2D空间中的点)时,不是单纯按照一个维度(如x坐标或y坐标)进行排序和分割,而是采用类似2d树(例如四叉树或八叉树)的方式来循环遍历不同维度。这意味着在插入、查找和更新节点的过程中,会依次根据每个维度的值来进行比较和操作,从而适应多维数据的特性,实现高效的搜索和维护。
高效且简单的用于处理k维数据的数据结构。
- 广泛应用。
该数据结构在众多领域和场景中得到广泛应用。 - 对高维度及聚类数据具有良好适应性。
这种数据结构尤其擅长处理高维度数据,并且对于具有聚类特性的数据集也能展现出很好的适应性能。 - 由一名本科算法课程学生发现!(Jon Bentley 在斯坦福大学读本科时)
这个高效的、简洁的数据结构的诞生源于一位在算法课程学习期间有所创新与发现的本科生。
3.8:N体模拟(物理学经典问题)
Appel算法:
关键思想:假定一个粒子远离一群粒子簇。
- 将粒子簇视为单一的集合体粒子。
当某个粒子距离其他大量粒子组成的集群非常远时,我们可以将这一整个粒子簇当作是一个单一的、具有代表性的大粒子来处理。 - 计算该粒子与集合体质心之间的力。
在这种简化情况下,仅计算这个孤立粒子与被看作单一粒子的粒子簇质心之间的相互作用力,而非分别计算它与簇内每一个粒子的力。
- 构建一个以N个粒子作为节点的3D树。
首先创建一个三维空间分割数据结构(3D树),并将所有N个粒子作为这个树的不同节点。 - 在每个节点存储其子树的质心信息。
对于树中的每一个节点,计算并储存该节点所代表的粒子子集的质心坐标。 - 计算单个粒子受到的总力时,遍历这棵树,但当粒子与当前子区域之间的距离足够大时停止搜索。
在求解某个特定粒子受到的所有其他粒子作用力之和时,通过遍历3D树进行搜索。然而,在遍历过程中,一旦检测到粒子与当前正在检查的子树区域间的距离超过了预先设定的阈值(即距离足够远以至于可忽略其余部分对目标粒子的影响),则提前终止对该子树剩余部分的遍历。
影响:每步的运行时间为 N log N ⇒ 可以进行新的研究。
(未完待续)