题目描述

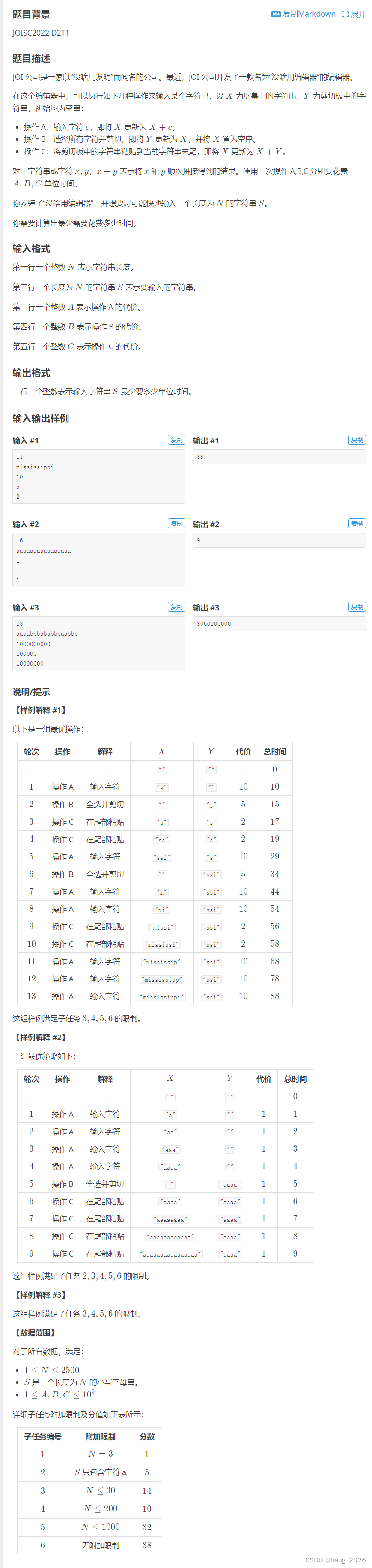
题面

分析

       这道题考场没有任何头绪，赛后也是看了许多题解才明白状态设计和转移的一步步思考过程。

       首先我们需要想到 无论是屏幕上的字符串，还是剪切板上的字符串，在任何时候都必须是目标串的子串。这个非常好像，如果不是目标串的子串，那么后期一定要再花费代价将它们改回来，这样一定不是最优的。因此，基于这个性质，我们可以设出一个四维状态： $d{p}_{l_x,r_x,l_y,r_y}$ 表示当前屏幕上的串是目标串的 $[l_x,r_x]$ 区间，剪切板上的串是目标串的 $[l_y,r_y]$ 区间的最小代价。

       那么显然有转移：

• $d{p}_{l_x,r_x,l_y,r_y}+A\to d{p}_{l_x-1,r_x,l_y,r_y}$ ，$d{p}_{l_x,r_x,l_y,r_y}+A\to d{p}_{l_x,r_x+1,l_y,r_y}$ ①
• $d{p}_{lx,rx,ly,ry}+B\to d{p}_{l_x,r_x+(r_y-l_y+1)}$ (当且仅当$[S_{rx+1},S_{rx+(ry-ly+1)}]=[S_{ly},S_{ry}]$， $S$ 为目标串)。②
• $d{p}_{lx,rx,ly,ry}+C\to d{p}_{0,0,lx,rx}$③

       这样的四维状态复杂度过高，$l_x$ 与 $r_x$ 显然去不掉，我们考虑怎样去掉 $l_y$ 和 $r_y$ 这两维。我们尝试 合并 第一个转移和第二个转移。也就是说，我们将转移修改为 对于一个串，先进行一次③操作，然后进行若干次①操作②操作，顺序随意得到一个新串。那么我们就得到了一个新的状态设计和转移：

       设 $d{p}_{l,r}$ 表示得到屏幕上的串为 $[S_l,S_r]$ 的最小代价。并且规定下一步转移要先剪切，再通过若干次添加和复制得到新串。 那么答案就是 $d{p}_{1,n}$。

       接着，我们考虑转移：

• $d{p}_{l,r}+A\to d{p}_{l-1,r}$， $d{p}_{l,r}+A\to d{p}_{l,r+1}$。①
• $d{p}_{l,r}+B+C\times k+A\times (r-p+1-k\times (r-l+1))\to d{p}_{p,r}$（需要满足 $[S_p,S_r]$ 中最多有 $k$ 个不想交$[S_l,S_r]$，$p$ 是满足这个条件最靠右的位置）。②

       这里解释一下几个问题：

       $Q_1:$ 第一个转移的含义不是在 $[l,r]$ 上直接添加字符得到新串吗？这样不是跟状态的定义不相符吗？

       $A_1:$ 这个转移是必要的，它虽然与我们的定义稍有不符，但这个转移一定没有错的。我们加上它可以覆盖到所有情况，不加的话会有情况取不到最优值。

       $Q_2:$ 为什么转移的时候右端点不用变？$d{p}_{l,r}$ 不是也能够往 右端点向右移的区间转移吗？

       $A_2：$ 我们考虑如果右端点右移得到新区间的右端点为 $q$，那么如果 $[S_r,S_q]$ 不包含 $[S_l,S_r]$，那么它一定可以由 $d{p}_{l,r}$ 通过若干步①转移过来。这也说明了①转移的必要性。如果 $[S_r,S_q]$ 包含 $[S_l,S_r]$ 那么它一定可以有更靠右的和$[S_l,S_r]$ 相等的字符串区间由②转移的到。因此只用改变左端点就好了。

       我们还需要解决一个问题，就是转移时如何求出下一个 $p$。我们可以预处理一个 $pr{e}_{l,r}$ 数组，表示 与$[l,r]$字符串相等，并且与$[l,r]$不交的最靠右的区间 $[p,q]$ 的右端点，也就是 $pre[l,r]$ 的值为 $q$。我们首先进行 字符串hash，那么 hash 值的种类最多 $n^2$ 个，我们对每一种 $hash$ 值开一个 $vector$ 存 对应区间的右端点。那么 $pre$ 数组就可以在 $vector$ 里面二分求解。

       时间复杂度 $O(n^2\ln n)$。

CODE：

#include<bits/stdc++.h>
#define pb push_back
using namespace std;
typedef unsigned long long ull;
typedef long long LL;
const int N = 2550;
const int M = N * N;
map< ull, int > mp;
vector< int > pos[M];
char str[N];
struct Hash {ull val; int rk, last;
}h[M];
int n, rk, pre[N][N], head[M], tot; // pre[l][r] 表示 l 前面第一个与 [Sl, Sr] 相等的字符串的右端点，并且没有交集
ull base = 1331, S[N], b[N], p = 1000037;
LL A, B, C, dp[N][N]; // dp[l][r]表示生成 [l, r] 的最小值 
ull calc(int l, int r) {return S[r] - S[l - 1] * b[r - l + 1];
}
int Find(int idx, int c) {int l = 0, r = pos[idx].size() - 1, mid, res = 0;while(l <= r) {mid = (l + r >> 1);if(pos[idx][mid] <= c) res = pos[idx][mid], l = mid + 1;else r = mid - 1;}return res;
}
void ins(ull val, int rk) {ull k = val % p;h[++ tot].last = head[k];h[tot].val = val;h[tot].rk = rk;head[k] = tot;
}
int GET(ull val) {ull k = val % p;for(int i = head[k]; i; i = h[i].last) {if(h[i].val == val) return h[i].rk;}return 0;
}
void get_pre() {for(int r = 1; r <= n; r ++ ) for(int l = 1; l <= r; l ++ ) if(!GET(calc(l, r))) ins(calc(l, r), ++rk);for(int r = 1; r <= n; r ++ ) {for(int l = 1; l <= r; l ++ ) {ull val = calc(l, r);pre[l][r] = Find(GET(val), l - 1);pos[GET(val)].pb(r);}}
}
void DP() {memset(dp, 0x3f, sizeof dp);for(int i = 1; i <= n; i ++ ) dp[i][i] = A;for(int len = 1; len < n; len ++ ) {for(int L = 1; L + len - 1 <= n; L ++ ) {int R = L + len - 1; // dp[L][R]dp[L][R + 1] = min(dp[L][R + 1], dp[L][R] + A);dp[L - 1][R] = min(dp[L - 1][R], dp[L][R] + A);int p = pre[L][R];LL cnt = 1;while(p) {int lp = p - len + 1;cnt ++;dp[lp][R] = min(dp[lp][R], dp[L][R] + B + cnt * C + (1LL * R - lp + 1 - cnt * len) * A);p = pre[lp][p];}}}printf("%lld\n", dp[1][n]);
}
int main() {scanf("%d", &n);scanf("%s", str + 1);scanf("%lld%lld%lld", &A, &B, &C);b[0] = 1;for(int i = 1; i <= n; i ++ ) b[i] = b[i - 1] * base;for(int i = 1; i <= n; i ++ ) {S[i] = S[i - 1] * base + (ull)(str[i]);}get_pre();DP();return 0;
}