曾梦想执剑走天涯,我是程序猿【AK】
目录
- 简述概要
- 知识图谱
- 1. K-Means聚类
- 2. 层次聚类(Hierarchical Clustering)
- 3. DBSCAN(Density-Based Spatial Clustering of Applications with Noise)
- 4. 谱聚类(Spectral Clustering)
- 评估聚类效果
简述概要
了解无监督学习之聚类
知识图谱
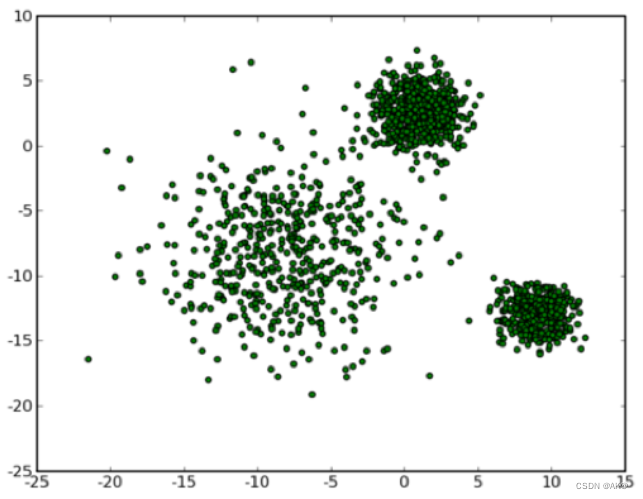
无监督学习中的聚类是一种将数据集中的对象分组的算法,使得同一组(簇)内的对象比其他组的对象更相似。聚类的目标是发现数据中的内在结构,而不是基于预先定义的标签。以下是几种常见的聚类算法及其原理:
1. K-Means聚类
K-Means是最常用的聚类算法之一。它的目标是将数据点划分为K个簇,使得每个簇内的点之间的距离尽可能小,而簇间的距离尽可能大。
-
算法步骤:
- 随机选择K个数据点作为初始的簇中心(质心)。
- 将每个数据点分配给最近的簇中心,形成K个簇。
- 重新计算每个簇的质心,即簇内所有点的均值。
- 重复步骤2和3,直到簇中心不再发生变化或达到预定的迭代次数。
-
优点:简单、易于实现,计算效率相对较高。
-
缺点:需要预先指定K值,对初始质心选择敏感,可能收敛到局部最优解。
2. 层次聚类(Hierarchical Clustering)
层次聚类通过构建一个层次结构来组织数据点,可以生成树状图(树状图)来表示数据点之间的层次关系。
-
算法步骤:
- 将每个数据点视为一个单独的簇。
- 计算所有簇之间的距离,合并距离最近的两个簇。
- 更新簇的距离矩阵。
- 重复步骤2和3,直到所有数据点合并为一个簇。
-
优点:不需要预先指定簇的数量,可以生成树状图来展示数据结构。
-
缺点:计算复杂度较高,不适合大规模数据集。
3. DBSCAN(Density-Based Spatial Clustering of Applications with Noise)
DBSCAN是一种基于密度的聚类算法,它可以发现任意形状的簇,并且能够识别噪声点。
-
算法步骤:
- 对于每个数据点,计算其邻域(在给定半径ε内)内的点数。
- 如果一个点的邻域内点数超过某个阈值minPts,则将其标记为核心点。
- 将所有直接密度可达的核心点归为一个簇,并递归地将所有从核心点可达的点加入该簇。
- 重复步骤3,直到没有新的点可以加入任何簇。
-
优点:能够处理噪声和异常值,发现任意形状的簇。
-
缺点:对参数ε和minPts的选择敏感,可能难以确定最佳参数。
4. 谱聚类(Spectral Clustering)
谱聚类是一种基于图论的聚类方法,它通过分析数据的相似性矩阵的特征来发现簇。
-
算法步骤:
- 构建数据的相似性矩阵,通常使用高斯相似性函数。
- 对相似性矩阵进行归一化处理,得到邻接矩阵。
- 计算邻接矩阵的特征值和特征向量,选择前K个最大的特征值对应的特征向量。
- 在这些特征向量上应用K-Means或其他聚类算法。
-
优点:能够发现任意形状的簇,对噪声不敏感。
-
缺点:计算复杂度较高,需要选择合适的相似性函数和邻接矩阵的构建方法。
评估聚类效果
聚类效果的评估通常依赖于一些指标,如轮廓系数(Silhouette Coefficient)、戴维斯-邦丁指数(Davies-Bouldin Index)和Calinski-Harabasz指数等。这些指标可以帮助我们理解簇的紧密程度和分离程度。
在实际应用中,选择合适的聚类算法和参数需要根据数据的特性和具体问题来决定。此外,聚类结果的解释和验证也是聚类分析中的重要步骤。在Java中,可以使用如Weka、Apache Mahout等库来实现上述聚类算法。
---- 永不磨灭的番号:我是AK