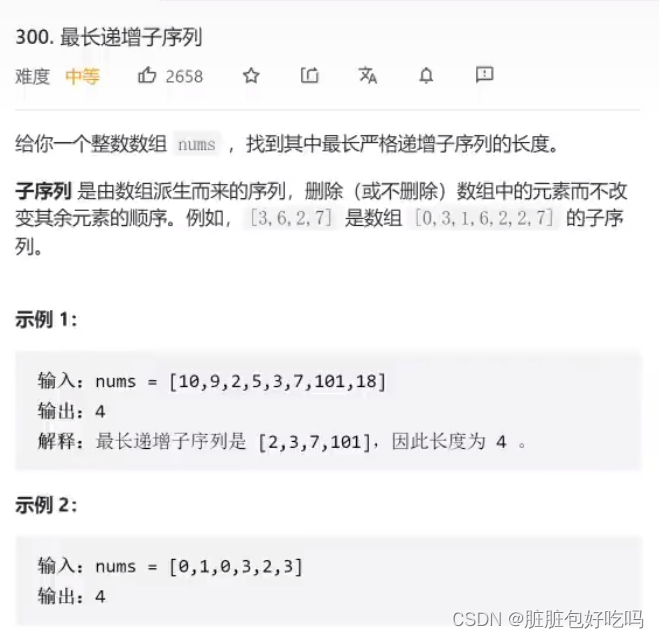
最长递增子序列
思路
- 定义状态:
- 我们定义一个数组
dp,其中dp[i]表示以nums[i]结尾的最长递增子序列的长度。
- 我们定义一个数组
- 初始化状态:
- 对于数组中的每个元素
nums[i],初始时都可以被视为一个长度为1的递增子序列,因此dp[i]的初始值都设为1。
- 对于数组中的每个元素
- 状态转移方程:
- 对于数组中的每个位置
i,我们遍历它之前的所有位置j(j < i)。 - 如果
nums[i]大于nums[j],说明nums[i]可以接在以nums[j]结尾的递增子序列后面,形成一个更长的递增子序列。 - 在这种情况下,我们可以更新
dp[i]为dp[j] + 1,表示以nums[i]结尾的递增子序列长度是以nums[j]结尾的子序列长度加1。 - 我们需要遍历所有
j < i的情况,并取dp[j] + 1中的最大值来更新dp[i]。
- 对于数组中的每个位置
- 求解结果:
- 在完成所有状态转移后,
dp数组中的最大值就是最长递增子序列的长度。 - 因为
dp[i]存储的是以nums[i]结尾的最长递增子序列的长度,所以最长递增子序列的实际长度可能不在数组末尾,而是在数组中的某个位置。 - 因此,我们需要遍历整个
dp数组来找到最大值,这个最大值就是最长递增子序列的长度。
- 在完成所有状态转移后,
- 优化空间复杂度:
- 上述方法的空间复杂度是 O(n),因为我们需要一个大小为 n 的
dp数组来存储状态。 - 但实际上,我们只需要知道前一个状态
dp[j]的值来更新当前状态dp[i],因此可以使用一个变量来替代整个数组,从而将空间复杂度优化到 O(1)。
- 上述方法的空间复杂度是 O(n),因为我们需要一个大小为 n 的
- 实现细节:
- 在实际编码时,我们需要处理边界情况,比如输入数组为空或只有一个元素的情况。
- 在
main方法中,我们需要创建LongestIncreasingSubsequence类的实例,并调用其lengthOfLIS方法来获取结果。
代码
import java.util.Scanner;
//给你一个整数数组nums,
//找到其中最长严格递增子序列的长度
public class 最长递增子序列 {//写一个方法public int lengthOfLIS(int [] nums) {//在方法的开始,我们首先处理边界情况if(nums==null || nums.length==0) {return 0;}//dp[i]将存储以nums[i]结尾的最长递增子序列的长度。int[] dp=new int[nums.length];//初始化一个变量maxLength,用于跟踪目前为止找到的最长递增子序列的长度int maxLength=1;for(int i=0;i<nums.length;i++) {dp[i]=1;//将dp[i]初始化为1,因为任何元素都可以作为一个长度为1的递增子序列。for(int j=0;j<i;j++) {//再用一个内层for循环遍历当前元素之前的所有元素。//在内层循环中,我们检查当前元素nums[i]是否大于前面的元素nums[j]if(nums[i]>nums[j]) {dp[i] = Math.max(dp[i], dp[j]+1);}}maxLength=Math.max(maxLength, dp[i]);}return maxLength;}public static void main(String[] args) {Scanner scan = new Scanner(System.in);最长递增子序列 ss =new 最长递增子序列();int [] nums= {10,9,2,5,3,7,101,18};int result = ss.lengthOfLIS(nums);System.out.println(result); }
}
最长递增子序列的个数

代码
import java.util.Arrays;public class 最长递增子序列的个数 {public int findNumberOfLIS(int[] nums) {if(nums==null || nums.length==0) {return 0;}int n=nums.length;int[] dp=new int[n];//dp[i] 存储以 nums[i] 结尾的最长递增子序列的长度int[] count = new int[n];//count[i] 存储以 nums[i] 结尾的最长递增子序列的个数Arrays.fill(count, 1);//初始化count数组,每个元素的最长递增子序列至少包含一个元素int maxLength = 1;//最长递增子序列的长度for(int i=0;i<n;i++) {dp[i]=1;for(int j=0;j<i;j++) {if(nums[i]>nums[j]) {if(dp[j]+1>dp[i]) {//如果发现一个更长的递增子序列,更新 dp[i] 并重置 count[i] dp[i]=dp[j]+1;count[i]=count[j];}else if(dp[j]+1==dp[i]){count[i] += count[j];}}}maxLength = Math.max(maxLength, dp[i]);}int result=0;for(int i=0;i<n;i++) {if(dp[i]==maxLength) {result+=count[i];}}return result;}public static void main(String[] args) {最长递增子序列的个数 solution=new 最长递增子序列的个数();int [] nums= {1,3,5,4,7};int count=solution.findNumberOfLIS(nums);System.out.println(count);}}知识点
Arrays.fill(count, 1);
是 Java 中的一个方法调用,用于将数组 count 的所有元素设置为指定的值,即 1。这个方法来自于 java.util.Arrays 类,是一个静态工具类,提供了很多用于操作数组(例如排序、搜索、填充等)的静态方法。
在这个特定的情境下,Arrays.fill(count, 1); 被用来初始化 count 数组。由于我们正在计算最长递增子序列的个数,每个元素至少可以作为一个长度为 1 的递增子序列的结束元素。因此,count 数组的每一个位置都被设置为 1,意味着每个元素开始时都被视为一个独立的递增子序列。