YOLOv9详细解读，改进提升全面分析（附YOLOv9结构图）-编程知识

🥑 Welcome to Aedream同学 's blog! 🥑

文章目录

- 1. 概要
- - 1.1 模型结构上的改动:
  - 1.2 训练脚本上的改动：
- 2. 介绍
- - 2.1 背景
  - 2.2 主要贡献
- 3. 总体框架
- - 3.1 可编程梯度信息（PGI）
  - - 3.1.1 辅助可逆分支
    - 3.1.2 多级辅助信息
  - 3.2 Generalized ELAN
- 参考

✨✨✨✨立志真正解决大家问题，只写精品博客文章，感谢关注，共同进步✨✨✨✨

1. 概要

论文链接：👿 YOLOv9: Learning What You Want to Learn Using Programmable Gradient Information
代码链接：👿 https://github.com/WongKinYiu/yolov9/tree/main

YOLOv9与v4、v7为同作者，所以按照继承性来说，与YOLOv7的联系最紧密，而不是v8。

1.1 模型结构上的改动:

详细介绍PGI与GELAN

YOLOv7的辅助训练头Aux->PGI(CBLinear,CBFuse)
ELAN->GELAN
downsample

class ADown(nn.Module):def __init__(self, c1, c2):  # ch_in, ch_out, shortcut, kernels, groups, expandsuper().__init__()self.c = c2 // 2self.cv1 = Conv(c1 // 2, self.c, 3, 2, 1)self.cv2 = Conv(c1 // 2, self.c, 1, 1, 0)def forward(self, x):x = torch.nn.functional.avg_pool2d(x, 2, 1, 0, False, True)x1,x2 = x.chunk(2, 1)x1 = self.cv1(x1)x2 = torch.nn.functional.max_pool2d(x2, 3, 2, 1)x2 = self.cv2(x2)return torch.cat((x1, x2), 1)

锚框：Anchor Free
标签分配策略：TaskAilgnAssigner
损失函数：Loss:Ciou+dfl+bce

1.2 训练脚本上的改动：

Flat Cosine Lr 和 Cos Lr
Fixed Lr
EarlyStopping
close-mosaic
min-items
LION Optimizer

2. 介绍

2.1 背景

如今的深度学习方法重点关注如何设计最合适的目标函数，从而使得模型的预测结果能够最接近真实情况。同时，必须设计一个适当的架构，可以帮助获取足够的信息进行预测。然而，现有方法忽略了一个事实，即当输入数据经过逐层特征提取和空间变换时，大量信息将会丢失。

本文将深入研究数据通过深度网络传输时数据丢失的重要问题，即信息瓶颈和可逆函数。我们提出了 可编程梯度信息（PGI） 的概念，以应对深度网络实现多个目标所需的各种变化。PGI可以为目标任务提供完整的输入信息来计算目标函数，从而获得可靠的梯度信息来更新网络权重。此外，还设计了一种新的基于梯度路径规划的轻量级网络架构——广义高效层聚合网络（GELAN）。GELAN的架构证实了PGI在轻量级模型上取得了卓越的成果。

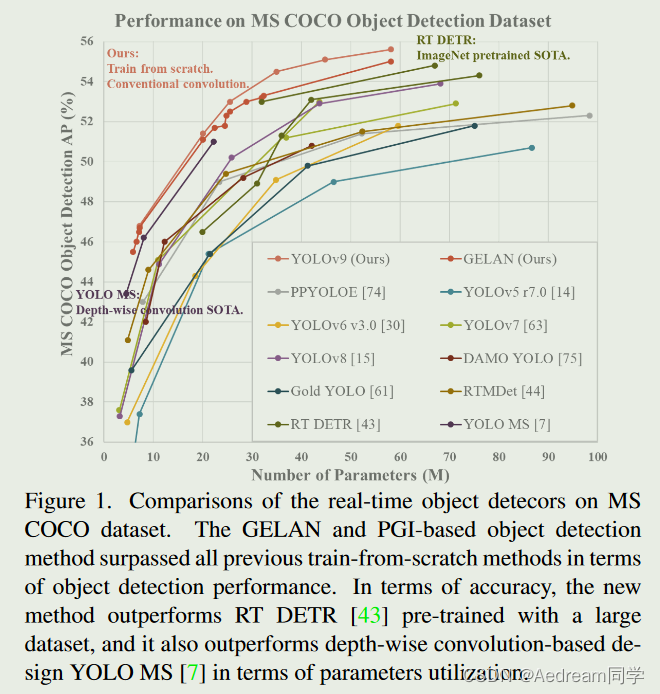
与基于深度卷积开发的最先进方法相比，GELAN仅使用传统的卷积算子来实现更好的参数利用率。PGI可以用于从轻量级到大型的各种模型。它可以用于获得完整的信息，因此从头开始训练的模型可以获得比使用大型数据集预先训练的现有模型更好的结果。

在这里插入图片描述

2.2 主要贡献

从可逆函数的角度对现有的深度神经网络架构进行了理论分析，并通过这个过程成功地解释了许多过去难以解释的现象。在此基础上，我们还设计了PGI和辅助可逆分支，并取得了良好的效果。
设计的PGI解决了深度监控只能用于极深度神经网络架构的问题，从而使新的轻量级架构能够真正应用于日常生活。
设计的GELAN仅使用传统卷积，比基于最先进技术的深度卷积设计实现了更高的参数使用率，同时显示出轻、快、准确的巨大优势。
将所提出的PGI和GELAN相结合，YOLOv9在MS COCO数据集上的目标检测性能在各个方面都大大超过了现有的实时目标检测器。

3. 总体框架

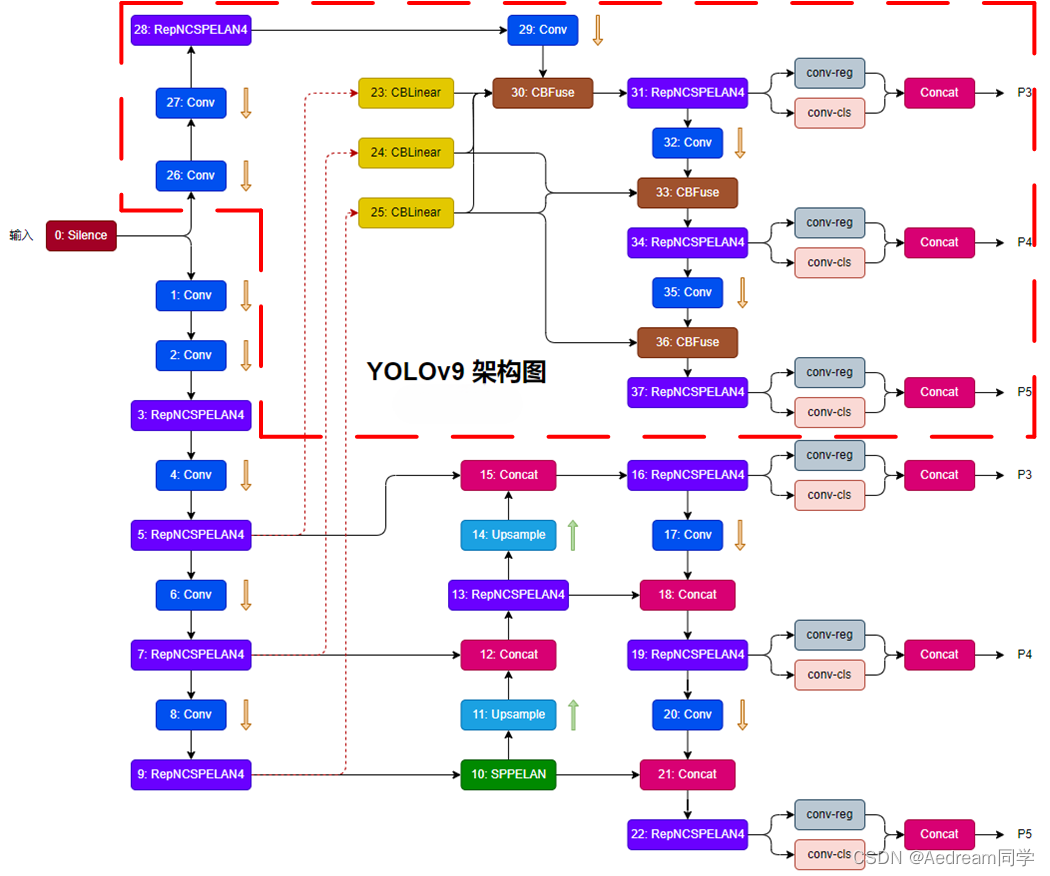
请添加图片描述

训练阶段：全部对应代码中models/detect/yolov9.yaml
推理阶段：下半部分对应代码中models/detect/gelan.yaml

3.1 可编程梯度信息（PGI）

Programmable Gradient Information
为了解决上述问题，我们提出了一种新的辅助监督框架，称为可编程梯度信息（PGI），如图3（d）所示。PGI主要包括三个部分，即（1）主分支、（2）辅助可逆分支和（3）多级辅助信息

PGI 的推理过程仅使用了主分支，因此不需要额外的推理成本；
辅助可逆分支是为了处理神经网络加深带来的问题，网络加深会造成信息瓶颈，导致损失函数无法生成可靠的梯度；
多级辅助信息旨在处理深度监督带来的误差累积问题，特别是多个预测分支的架构和轻量级模型。

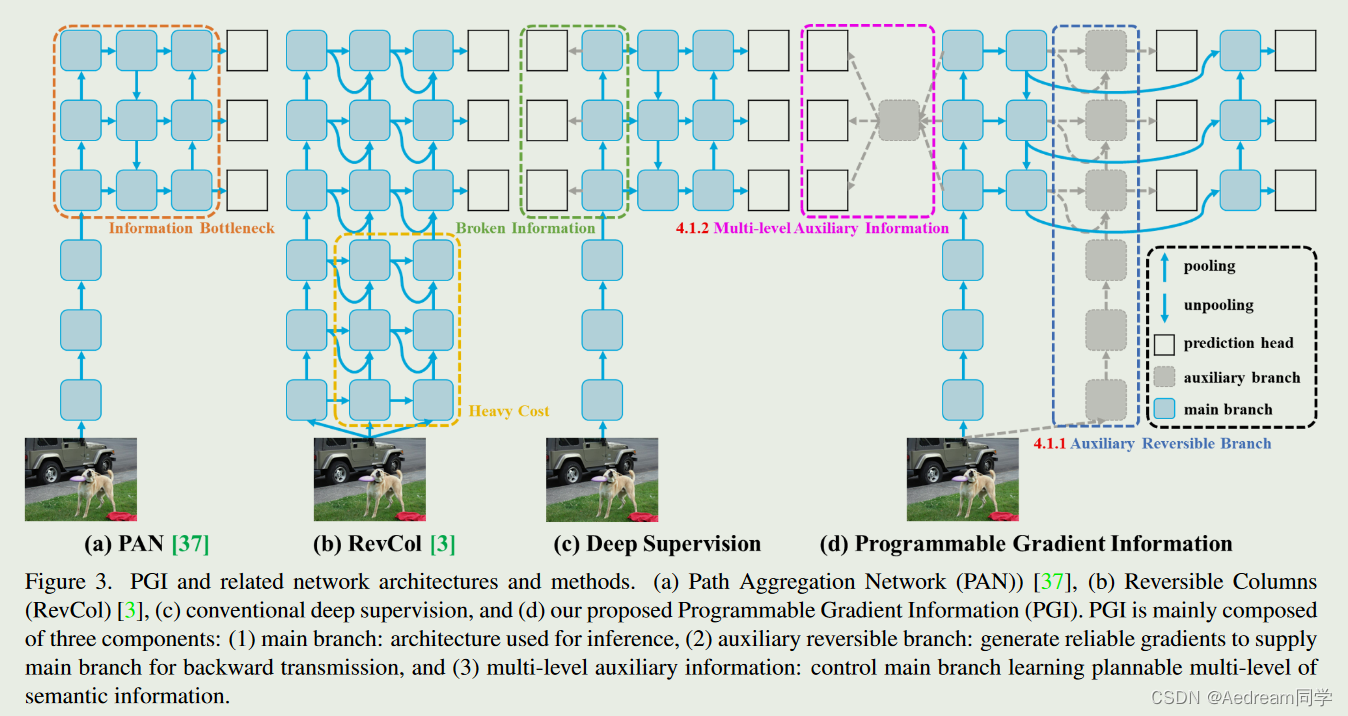
在这里插入图片描述

3.1.1 辅助可逆分支

Auxiliary Reversible Branch
在PGI中，我们提出了辅助可逆分支来生成可靠的梯度并更新网络参数。通过提供从数据映射到目标的信息，损失函数可以提供指导，并避免从与目标不太相关的不完整前馈特征中发现虚假相关性的可能性。我们提出通过引入可逆结构来维护完整信息，但在可逆结构中添加主分支将消耗大量的推理成本。我们分析了图3（b）的架构，发现当添加从深层到浅层的额外连接时，推理时间将增加20%。当我们反复将输入数据添加到网络的高分辨率计算层（黄色框）时，推理时间甚至超过了时间的两倍。

由于我们的目标是使用可逆结构来获得可靠的梯度，因此“可逆”并不是推理阶段的唯一必要条件。有鉴于此，我们将可逆分支视为深度监管分支的扩展，然后设计辅助可逆分支，如图3（d）所示。至于由于信息瓶颈而丢失重要信息的主要分支深层特征，它们将能够从辅助可逆分支接收可靠的梯度信息。这些梯度信息将驱动参数学习，以帮助提取正确和重要的信息，并且上述动作可以使主分支获得对目标任务更有效的特征。此外，可逆架构在浅层网络上的性能比在一般网络上差，因为复杂的任务需要在更深的网络中进行转换。我们提出的方法并不强迫主分支保留完整的原始信息，而是通过辅助监督机制生成有用的梯度来更新它。这种设计的优点是，所提出的方法也可以应用于较浅的网络。

最后，由于在推理阶段可以去除辅助可逆分支，因此可以保留原始网络的推理能力。我们也可以选择PGI中的任何可逆结构来发挥辅助可逆分支的作用。

3.1.2 多级辅助信息

Multi-level Auxiliary Information
在本节中，我们将讨论多级辅助信息是如何工作的。包括多个预测分支的深度监管架构如图3（c）所示。对于对象检测，不同的特征金字塔可以用于执行不同的任务，例如，它们可以一起检测不同大小的对象。因此，在连接到深度监督分支后，浅层特征将被引导学习小物体检测所需的特征，此时系统将把其他大小物体的位置作为背景。然而，上述行为将导致深度特征金字塔丢失预测目标对象所需的大量信息。关于这个问题，我们认为每个特征金字塔都需要接收关于所有目标对象的信息，以便后续的主分支能够保留完整的信息来学习对各种目标的预测。

多级辅助信息的概念是在辅助监督的特征金字塔层次层和主分支之间插入一个集成网络，然后使用它来组合来自不同预测头的返回梯度，如图3（d）所示。多级辅助信息是对包含所有目标对象的梯度信息进行聚合，并将其传递给主分支，然后更新参数。此时，主分支的特征金字塔层次结构的特征将不会被某些特定对象的信息所支配。因此，我们的方法可以缓解深度监管中的信息泄露问题。此外，任何集成网络都可以用于多级辅助信息。因此，我们可以规划所需的语义级别，以指导不同规模的网络架构的学习。

3.2 Generalized ELAN

YOLOv9将ELAN的能力进行了泛化，原始ELAN仅使用卷积层的堆叠，而GELAN可以使用任何计算块作为基础Module。

通俗来说：

查看代码可以发现，总体框架类似于把C3嵌入C2f，只是组成的基本模块不同而已。

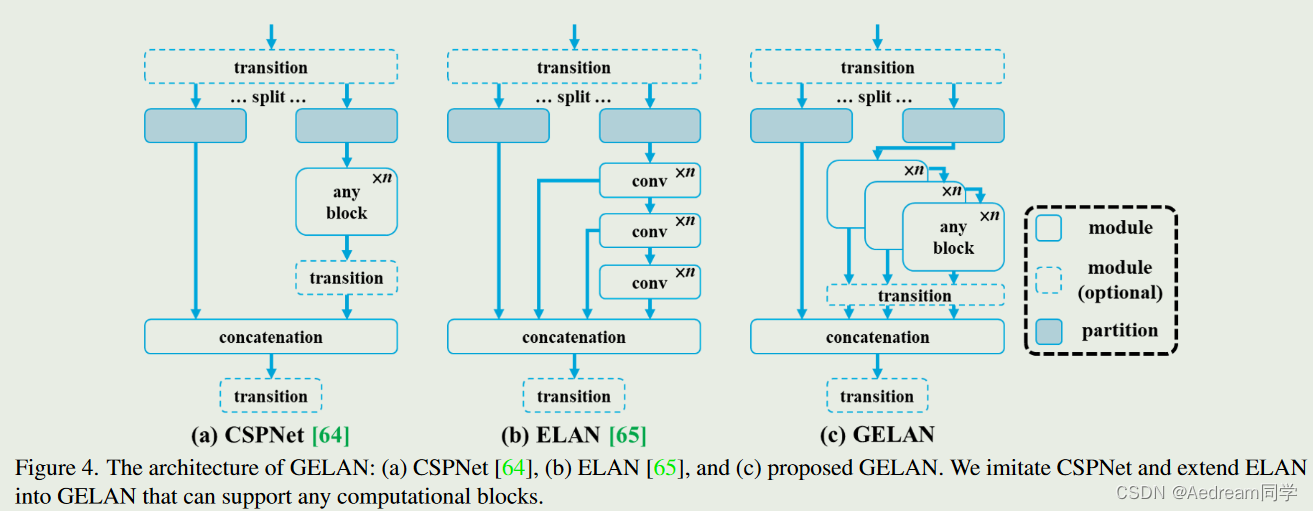
在本节中，我们将介绍拟议的新网络架构——GELAN。通过结合两种采用梯度路径规划设计的神经网络架构CSPNet和ELAN，我们设计了考虑重量、推理速度和准确性的广义有效层聚合网络（GELAN）。其总体架构如图4所示。我们将最初仅使用卷积层堆叠的ELAN[65]的能力推广到可以使用任何计算块的新架构。

在这里插入图片描述