梯度下降算法
在机器学习中,梯度下降算法常用于最小化代价函数(或损失函数),以此来优化模型的参数。代价函数衡量的是模型预测值与实际值之间的差异。通过最小化这个函数,我们可以找到模型预测最准确的参数。
代价函数
代价函数(Cost Function)或损失函数(Loss Function),是用来衡量模型预测值与真实值之间差异的一个函数。在回归问题中,一个常见的代价函数是均方误差
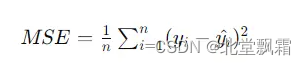
其中n是样本数量,yi是样本的真实值,被减去的则是预测值,这个值越小,说明预估越接近真实值。
实际案例:从简单线性回归理解梯度下降算法
假设我们有一组数据,表示房屋的大小与其价格的关系。我们想要构建一个简单的线性回归模型来预测房价,模型形式为
y=wx+b,其中 y 是房价,x 是房屋大小,w 是斜率,b 是截距。
第一步要做的是:初始化模型参数:随机选择w 和 b 的初始值,比如 w=0 和 b=0。计算代价函数的梯度:首先,我们需要定义代价函数,这里我们使用均方误差。然后,计算代价函数关于每个参数的梯度。
我们随意给出一组数据:
(1,2),(2,4),(3,6)
我们的目的是尽量用y=wx+b去拟合这些数据。w梯度计算公式是:
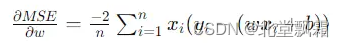
b的则是

w=0,b=0得出得梯度分别是: -56/3和 -8。
这个线性模型是一条 y=0的直线,显然无法拟合这些数据.我们此时设置 w=0.1,b=0.1来拟合,又得到了两个梯度,可能这次的线性模型拟合度会好一些,那么再设置w=0.2,b=0.2,会不会又好一点呢?我们每次选用w,b都会得到一个预测值,然后我们可以算出他的代价函数(误差)值,我们就可以画出这样一张图。

其中我们要找的点就是误差最低的那一个点,我们可能会从任何地方出发,去找那个点,这个过程运用到的就是梯度下降算法
正式介绍
通过上面那个小例子,我们已经知道了,梯度下降算法常用于最小化代价函数(或损失函数),以此来优化模型的参数。代价函数衡量的是模型预测值与实际值之间的差异。通过最小化这个函数,我们可以找到模型预测最准确的参数。
抽象
我们可以抽象这个过程:想象一下,你在山顶,目标是以最快的速度下到山脚。因为你被蒙上了眼睛,看不见周围的环境,所以你只能通过感觉脚下的坡度来判断下一步该往哪个方向走。这个“感觉坡度”的过程,就有点像梯度下降算法的工作原理。
梯度的含义
“梯度”(Gradient)其实就是指函数在某一点上的斜率,或者说是这一点最陡的上升方向。梯度告诉你,如果你想让函数值增加得最快,应该往哪个方向走。相应地,梯度的反方向就是函数值下降最快的方向。
梯度下降的工作原理
梯度下降算法的核心思想就是:在当前位置计算梯度(即斜率),然后沿着梯度的反方向走一小步,重复这个过程,直到到达山脚(即找到函数的最小值点)。
梯度下降–专属案例
假设我们有一个函数
y=x^2这个求最小值,这个案例不是让你使用高中数学去解答,你可以不假思索回答是0,但是不是我想要学习的。
让我们以梯度下降的方式求解,初始化: 假设我们随机选择一个起点,x=2。计算梯度: 对f(x) 求导得到它的梯度 f(x)=2x。在x=2 处的梯度是4。此时我们更新x,我们假设我们走一小步,0.1那么此时x应该是:x = x - 学习率 * 梯度 = 2 - 0.1 * 4 = 1.6 计算此时的梯度,重复这个过程,直到x的更新值很小很小,无限趋近于0,此时实际上x的值(在y=x^2中)也无限趋近于0,y也趋近于0了。
注意事项
学习率的选择:学习率太大可能导致“跨过”最低点,甚至发散;学习率太小又会导致收敛速度很慢。因此,选择一个合适的学习率非常关键。收敛条件:通常会设置一个阈值,当连续两次迭代的x值变化非常小(小于这个阈值)时,我们就认为算法已经收敛。
结束
我们计算房价,假设线性模型,求w,b,我们使用均方误差(MSE)作为代价函数,来衡量模型预测值与实际值之间的差异,我们使用梯度下降模型计算w,b的梯度,得到了误差,我们通过控制迭代次数和学习率,不断的修改w,b,以使得误差越来越小,误差越来越小,即w,b的变化非常小或达到一个预设的迭代次数。这就是梯度下降算法。对于不同类型的机器学习问题,成本函数的选择也会不同。例如:回归问题:常用的成本函数是均方误差(Mean Squared Error, MSE),它计算的是预测值与实际值之间差异的平方的平均值。这个值越小,表示模型的预测越准确。分类问题:对于二分类问题,一个常见的成本函数是交叉熵(Cross-Entropy),它量化的是实际标签与预测概率之间的差异。
在梯度下降算法中,我们的目标是找到模型参数的值,这些参数值能使成本函数的值最小化。换句话说,我们希望找到的参数能让模型的预测尽可能接近实际情况,从而最小化误差。通过迭代地更新模型参数,梯度下降算法能够逐步逼近这个最优参数组合,实现成本的最小化。