一、詹姆斯·麦昆（James MacQueen）

IMS研究员詹姆斯·B·麦昆于2014年7月15日病逝，享年85岁。他的妻子安和他们的三个孩子唐纳德、凯特和玛丽以及五个孙子孙女幸存下来。

从1962年到去世，麦昆教授一直在加州大学洛杉矶分校管理研究生院工作。1952年，他在俄勒冈州里德学院获得心理学学士学位，1954年和1958年分别在俄勒冈州大学获得理学硕士和心理学博士学位。在加入加州大学洛杉矶分校（UCLA）之前，麦昆教授有着杰出的职业生涯，包括在俄勒冈州大学（University of Oregon）和加州大学伯克利分校（University of California，Berkeley）以及加州大学洛杉矶分校（UCLA）西部管理科学研究所（Western Management Science Institute）与雅各布·马沙克教授（Jacob Marshak）担任学术。

吉姆的研究兴趣在于提供人类过程的数学公式。在1960年与鲁伯特·米勒（Rupert Miller）合著的第一篇重要论文[1]中，他研究了一大类最优停止问题。作为一个特例，本文首次提到了找房子的问题。在经济学中，这被称为求职问题或出售资产的问题，并引发了大量研究。

吉姆是另一个领域的先驱，他称之为k-means[2]的开发。这是一种通过将样本空间划分为k个类内方差较小的集合来检测多元数据中的聚类的方法。k的值也可由数据选择。

他的另一个有趣发明是吉姆所说的“线性鞅”[3]，朋友和同事们称之为“麦金格尔”。这是一个随机变量序列，根据过去的观察，下一次观察的预期是最近过去的固定线性组合。主要结果是Doob鞅收敛定理的一个显著推广。

在马尔可夫过程领域，吉姆特别喜欢建模马尔可夫链。在描述这样的链时，可以给出转移概率，也可以给出弧上的一组平衡权重。使用平衡权重的优点是，平稳分布（以及转移概率）可以很容易地推导出来。诀窍是以平衡、有意义的方式设置权重。在《电路过程》一文[4]中，Jim通过为链状态上的一组电路分配权重来实现这一点。这些想法在他的论文《马尔科夫雕塑》中以一种优美的方式展开[5]。

吉姆性格开朗，容易交到朋友，总是开朗幽默。他没有自尊心，总是乐于为他人争光。对于需要解决的问题，他善于提出新的想法，有时令人震惊。他喜欢户外活动，喜欢在怀俄明州的大角山徒步旅行。

他是洛杉矶、伯克利和学术会议上克里格斯皮尔的狂热球员。在克里格斯皮尔，他以敢于尝试新策略而闻名。劳埃德·夏普利曾经说过，他总是从扮演吉姆中学到一些东西。所有认识他的人都会怀念他聪明迷人的个性。

作者：托马斯·S·弗格森教授

加州大学洛杉矶分校数学与统计系

二、K均值聚类算法

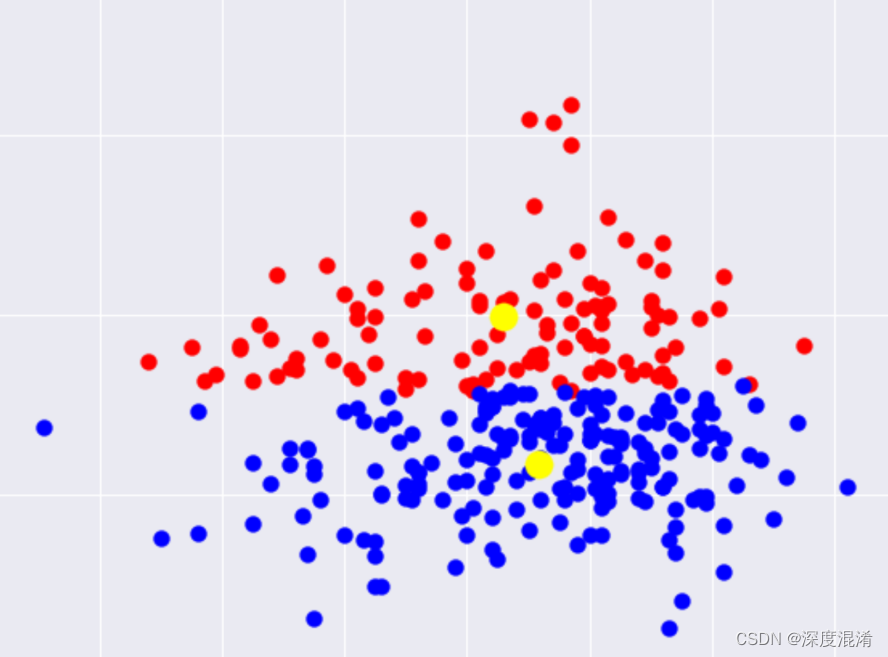
K均值聚类算法（K-Means Clustering Algorithm）是一种迭代求解的聚类分析算法，其步骤是，预将数据分为K组，则随机选取K个对象作为初始的聚类中心，然后计算每个对象与各个种子聚类中心之间的距离，把每个对象分配给距离它最近的聚类中心。聚类中心以及分配给它们的对象就代表一个聚类。每分配一个样本，聚类的聚类中心会根据聚类中现有的对象被重新计算。这个过程将不断重复直到满足某个终止条件。终止条件可以是没有（或最小数目）对象被重新分配给不同的聚类，没有（或最小数目）聚类中心再发生变化，误差平方和局部最小。

k均值聚类是使用最大期望算法（Expectation-Maximization algorithm）求解的高斯混合模型（Gaussian Mixture Model, GMM）在正态分布的协方差为单位矩阵，且隐变量的后验分布为一组狄拉克δ函数时所得到的特例。
 

using System; 
using System.Data; 
using System.Drawing;
using System.Collections;
using System.Collections.Generic;namespace Legalsoft.Truffer.Algorithm
{/// <summary>/// K-Means算法/// </summary>public class K_Means_Algorithm{private static int K { get; set; } = 0;private List<PointF> points { get; set; } = new List<PointF>();public K_Means_Algorithm(List<PointF> p, int k){K = k;points.AddRange(p);}/// <summary>/// 计算新的聚类中心 /// </summary>/// <param name="m"></param>/// <param name="type"></param>/// <returns></returns>public PointF Center_Point(int m, int[] type){int count = 0;PointF sum = new PointF(0.0F, 0.0F);for (int i = 0; i < points.Count; i++){if (type[i] == m){sum.X = points[i].X + sum.X;sum.Y = points[i].Y + sum.Y;count++;}}if (count > 0){sum.X = sum.X / count;sum.Y = sum.Y / count;}return sum;}/// <summary>/// 比较两个聚类中心的是否相等/// </summary>/// <param name="a"></param>/// <param name="b"></param>/// <returns></returns>private bool Compare(PointF a, PointF b){if (((int)(a.X * 10) == (int)(b.X * 10)) && ((int)(a.Y * 10) == (int)(b.Y * 10))){return true;}else{return false;}}/// <summary>/// 进行迭代，对total个样本根据聚类中心进行分类/// </summary>/// <param name="type"></param>/// <param name="z"></param>private void Order(ref int[] type, PointF[] z){//记录unknown[i]暂时在哪个类中 int temp = 0;for (int i = 0; i < points.Count; i++){for (int j = 0; j < K; j++){if (Distance(points[i], z[temp]) > Distance(points[i], z[j])){temp = j;}}type[i] = temp;}}/// <summary>/// 计算两个点的欧式距离/// </summary>/// <param name="p1"></param>/// <param name="p2"></param>/// <returns></returns>private float Distance(PointF p1, PointF p2){return ((p1.X - p2.X) * (p1.X - p2.X) + (p1.Y - p2.Y) * (p1.Y - p2.Y));}/// <summary>/// 进行聚类/// </summary>/// <returns></returns>public List<List<PointF>> Execute(){int[] type = new int[points.Count];PointF[] z = new PointF[K];PointF[] z0 = new PointF[K];for (int i = 0; i < K; i++){z[i] = points[i];}List<List<PointF>> result = new List<List<PointF>>();int test = 0;int loop = 0;while (test != K){Order(ref type, z);for (int i = 0; i < K; i++){z[i] = Center_Point(i, type);if (Compare(z[i], z0[i])){test = test + 1;}else{z0[i] = z[i];}}loop = loop + 1;List<PointF> p = new List<PointF>();for (int j = 0; j < K; j++){for (int i = 0; i < points.Count; i++){if (type[i] == j){p.Add(points[i]);}}}if (p.Count > 0){result.Add(p);}}return result;}}
}