PCL中的3D特征

理论入门

来自[RusuDissertation]：

在他们原生表示中， 点 如 3D 映射系统概念中定义的那样，使用它们的笛卡尔坐标 x、y、z 相对于给定原点简单地表示。假设坐标系的原点不随时间变化，则在 t1 和 t2 处获取的两个点 p1 和 p2 可能具有相同的坐标。然而，比较这些点是一个不适定的问题，因为即使它们在某些距离度量（例如欧几里德度量）方面相等，但它们可以在完全不同的表面上进行采样，因此当与其他点放在一起时代表完全不同的信息在他们附近的周围点。那是因为不能保证时间在 t1 和 t2 之间没有改变。一些采集设备可能会提供采样点的额外信息，

由于各种原因需要比较点的应用程序需要更好的特性和度量，以便能够区分几何表面。因此，作为具有笛卡尔坐标的单一实体的 3D 点的概念消失了， 取而代之的是一个新概念，即局部描述符** 。文献中有大量描述相同概念的不同命名方案，例如 形状描述符 或 几何特征， 但对于本文档的其余部分，它们将被称为 点特征表示。

…

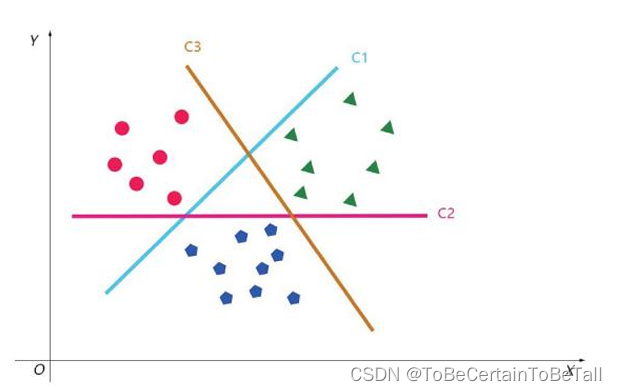
通过包括周围的邻居，可以在特征公式中推断和捕获底层采样表面几何形状，这有助于解决歧义比较问题。理想情况下，对于位于相同或相似表面上的点，结果特征将非常相似（相对于某些度量），而对于不同表面上的点，结果特征将非常相似，如下图所示。一个 好的 点特征表示与 坏的 点特征表示不同*，它能够在以下情况下捕获相同的局部表面特征：*

• 刚性变换——即数据中的 3D 旋转和 3D 平移不应影响合成特征向量 F 估计；
• 变化的采样密度-原则上，一个或多或少密集采样的局部表面补丁应该具有相同的特征向量签名；
• 噪声-在数据中存在轻微噪声的情况下，点特征表示必须在其特征向量中保留相同或非常相似的值。

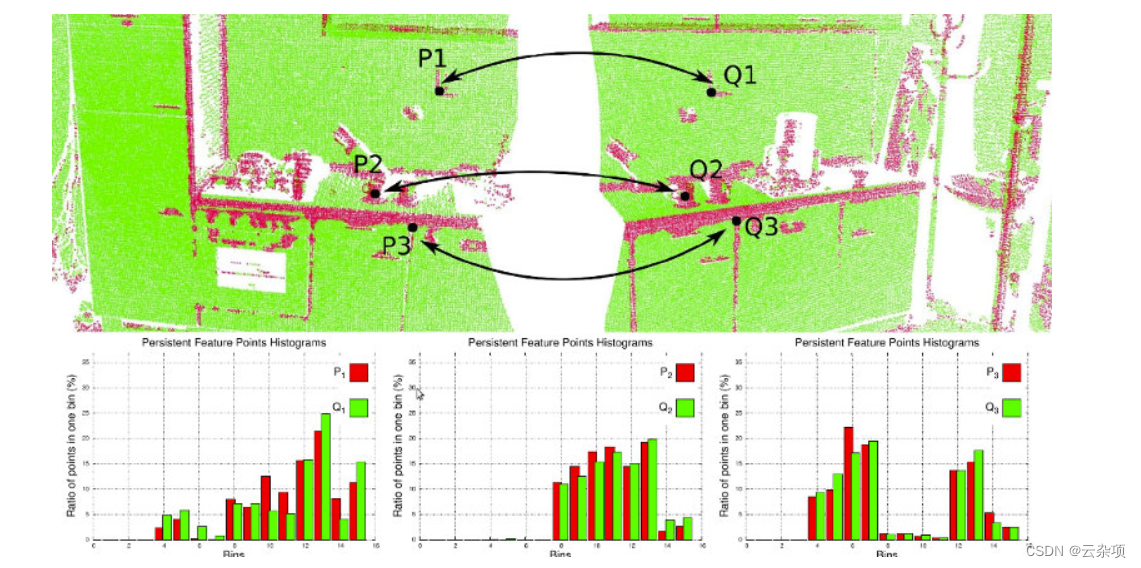
通常，PCL 特征使用近似方法来计算查询点的最近邻居，使用快速 kd 树查询。我们对两种类型的查询感兴趣：

• 确定查询点的k（用户给定参数）邻居（也称为k-search）；
• 确定一个查询点在半径为r的球体内的所有邻居（也称为radius-search）。

注意：

有关正确的k或r值应该是什么的讨论，请参阅pclpy OC-Tree “体素内的邻居搜索”、“K 最近邻搜索”和“半径内的邻居搜索”-CSDN博客。

如何传递输入

由于 PCL 中几乎所有类都继承自基本pcl::PCLBase类，因此pcl::Feature类以两种不同的方式接受输入数据：

1. 一个完整的点云数据集，通过setInputCloud (PointCloudConstPtr &) -强制

   任何特征估计类都将尝试估计给定输入云中每个点的特征。

2. 点云数据集的子集，通过setInputCloud (PointCloudConstPtr &)和setIndices (IndicesConstPtr &) 给出-可选

   任何特征估计类都将尝试估计给定输入云中每个点的特征，该点在给定索引列表中具有索引。默认情况下，如果没有给出一组索引，则将考虑云中的所有点。

此外，可以通过附加调用**setSearchSurface (PointCloudConstPtr &)**指定要使用的点邻居集。此调用是可选的，当未给出搜索面时，默认使用输入点云数据集。

因为**setInputCloud()*总是需要的，所以我们可以使用<setInputCloud(), setIndices(), setSearchSurface()>*创建最多四种组合。假设我们有两个点云，P={p_1, p_2, …p_n} 和 Q={q_1, q_2, …, q_n}。下图显示了所有四种情况：

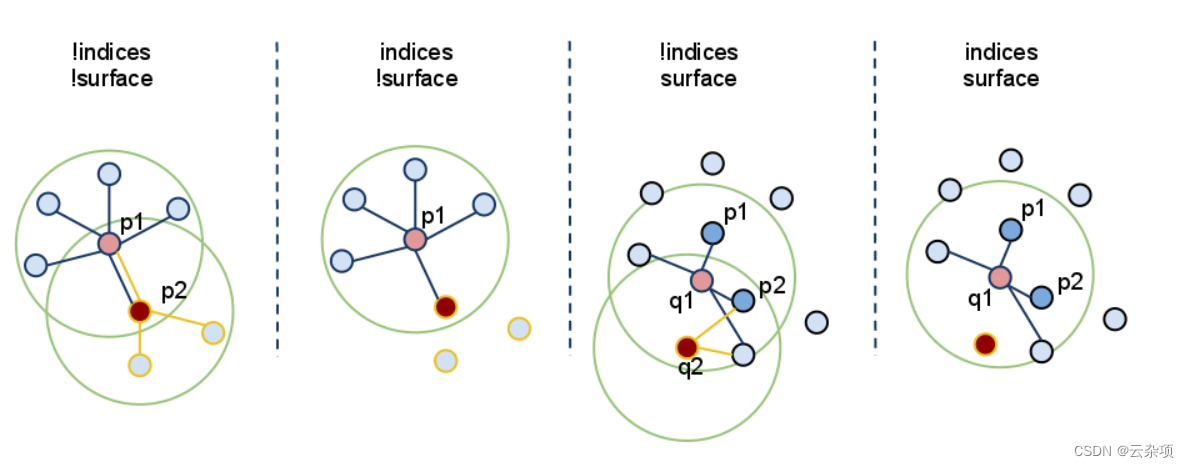
• setIndices() = false, setSearchSurface() = false - 这无疑是 PCL 中最常用的情况，其中用户只是输入单个 PointCloud 数据集并期望在云中的所有点估计某个特征。

  由于我们不希望根据是否给出一组索引和/或搜索表面来维护不同的实现副本，因此每当索引 = false 时，PCL 都会创建一组内部索引（作为std::vector）基本上指向整个数据集（索引=1…N，其中 N 是云中的点数）。

  在上图中，这对应于最左边的情况。首先，我们估计 p_1 的最近邻居，然后是 p_2 的最近邻居，依此类推，直到我们用尽 P 中的所有点。

• setIndices() = true, setSearchSurface() = false - 如前所述，特征估计方法只会计算那些在给定索引向量中有索引的点的特征；

  在上图中，这对应于第二种情况。在这里，我们假设 p_2 的索引不是给定的索引向量的一部分，因此不会在 p2 估计邻居或特征。

• setIndices() = false, setSearchSurface() = true - 与第一种情况一样，将对作为输入给出的所有点的特征进行估计，但是，在setSearchSurface() 中给出的底层相邻表面将用于获取输入的最近邻点，而不是输入云本身；

  在上图中，这对应于第三种情况。如果 Q={q_1, q_2} 是另一个作为输入给出的云，不同于 P，并且 P 是 Q 的搜索表面，那么 q_1 和 q_2 的邻居将从 P 计算。

• setIndices() = true, setSearchSurface() = true - 这可能是最罕见的情况，其中索引和搜索表面都被给出。在这种情况下，将使用setSearchSurface() 中给出的搜索表面信息，仅为<input,indices> 对中的一个子集估计特征。

  最后，在上图中，这对应于最后一个（最右边）的情况。在这里，我们假设 q_2 的索引不是为 Q 给出的索引向量的一部分，因此不会在 q2 估计邻居或特征。

应该使用**setSearchSurface()**时最有用的例子是，当我们有一个非常密集的输入数据集，但我们不想估计其中所有点的特征，而是估计使用pcl_keypoints 中的方法发现的某些关键点=时，或者在云的下采样版本（例如，使用pcl::VoxelGrid过滤器获得）。在这种情况下，我们通过setInputCloud()传递下采样/关键点输入，并将原始数据作为setSearchSurface() 传递。

法线估计例子

输入一旦确定，就可使用查询点的相邻点来估计局部特征表示，这表示捕获查询点周围的底层采样表面的几何形状。描述表面几何形状的一个重要问题是首先推断其在坐标系中的方向，即估计其法线。表面法线是表面的重要属性，在许多领域（例如计算机图形应用程序）中大量使用，以应用生成阴影和其他视觉效果的正确光源（有关更多信息，请参阅[RusuDissertation]）。

from pclpy import pcldef multiCloudShow(cloud1, cloud2):"""Args:多点云可视化在同一个窗口cloud1:  点云数据cloud2:  点云数据"""viewer = pcl.visualization.PCLVisualizer("viewer")  # 建立可刷窗口对象 窗口名 viewersingle_color = pcl.visualization.PointCloudColorHandlerCustom.PointXYZ(cloud1, 255.0, 0, 0.0)  # 将点云设置为红色viewer.addPointCloud(cloud1,  # 要添加到窗口的点云数据。single_color,  # 指定点云的颜色"sample cloud1",  # 添加的点云命名)  # 点云添加到的视图single_color = pcl.visualization.PointCloudColorHandlerCustom.PointXYZ(cloud2, 0.0, 255.0, 0.0)  # 将点云设置为绿色viewer.addPointCloud(cloud2,  # 要添加到窗口的点云数据。single_color,  # 指定点云的颜色"sample cloud2",  # 添加的点云命名)  # 点云添加到的视图# 窗口建立while not viewer.wasStopped():viewer.spinOnce(10)if __name__ == '__main__':# 加载点云cloud = pcl.PointCloud.PointXYZ()reader = pcl.io.PCDReader()reader.read("res/table_scene_lms400.pcd", cloud)# 估计法线# 为输入数据集中的所有点估计一组表面法线ne = pcl.features.NormalEstimation.PointXYZ_Normal()ne.setInputCloud(cloud)tree = pcl.search.KdTree.PointXYZ()   # 建立kd树ne.setSearchMethod(tree)cloud_normals = pcl.PointCloud.Normal()  # 法线对象ne.setRadiusSearch(0.003)  # 搜索半径为 0.0003ne.compute(cloud_normals)  # 计算法线print(cloud_normals.size())# 为输入数据集中的点子集估计一组表面法线。ne = pcl.features.NormalEstimation.PointXYZ_Normal()ne.setInputCloud(cloud)tree = pcl.search.KdTree.PointXYZ()ne.setSearchMethod(tree)ind = pcl.PointIndices()[ind.indices.append(i) for i in range(0, cloud.size() // 2)]  # 去点云的下标ne.setIndices(ind)  # 将下标进行提取得的点云cloud_normals = pcl.PointCloud.Normal()ne.setRadiusSearch(0.003)ne.compute(cloud_normals)print(cloud_normals.size())# 为输入数据集中的所有点估计一组表面法线，但使用另一个数据集估计它们的最近邻ne = pcl.features.NormalEstimation.PointXYZ_Normal()cloud_downsampled = pcl.PointCloud.PointXYZ()  # 获取一个降采样的点云 方法比较多，这里使用voxelized方法vox = pcl.filters.VoxelGrid.PointXYZ()vox.setInputCloud(cloud)vox.setLeafSize(0.005, 0.005, 0.005)  # 0.005*0.005*0.005 内保存一个点云vox.filter(cloud_downsampled)ne.setInputCloud(cloud_downsampled)ne.setSearchSurface(cloud)tree = pcl.search.KdTree.PointXYZ()ne.setSearchMethod(tree)cloud_normals = pcl.PointCloud.Normal()ne.setRadiusSearch(0.003)ne.compute(cloud_normals)print(cloud_normals.size())