---

一、Nim游戏

1.1问题描述

甲，乙两个人玩 nim 取石子游戏。

nim 游戏的规则是这样的：地上有 n 堆石子（每堆石子数量小于 10^4），每人每次可从任意一堆石子里取出任意多枚石子扔掉，可以取完，不能不取。每次只能从一堆里取。最后没石子可取的人就输了。假如甲是先手，且告诉你这 n 堆石子的数量，他想知道是否存在先手必胜的策略。

上面这种游戏被称为NIM博弈。对于游戏过程中面临的状态，如果玩家在这种状态下无论进行任何行动，都会输掉游戏，我们称该状态为必败态。同样的，如果玩家在这种状态下无论进行任何行动，都会赢得游戏，我们称该状态为必胜态。

1.2定理

1.2.1定理内容

NIM博弈先手必胜，当且仅当 A1 ^ A2 ^ …… ^ An ≠ 0

1.2.2定理证明

下面采用的证明方法是NIM博弈问题常用证明方法：

• 证明：必胜态的后继状态至少存在一个必败态
  • 若A1 ^ A2 ^ …… ^ An = s，设s最高位是第k位，则A1~An中有奇数个第k位为1，不妨从中取出Ai，那么Ai ^ s <= Ai
  • 我们可以减少Ai为Ai ^ s，那么此时有A1 ^ A2 ^ … ^ Ai ^ s ^ … ^ An = s ^ s = 0
  • 于是就得到了一个必败态
• 证明：必败态的后继状态均为必胜态
  • 由于A1 ^ A2 ^ …… ^ An = 0，于是所有位置上1的个数为偶数
  • 无论我们取走哪一堆，都会使某一位上1的个数为奇数，从而得到必胜态

因此必胜态和必败态必然交替出现，先手者若以必胜态开局，总能使得自己处于不败之地，直到对手失败。

1.3OJ练习

1.3.1模板OJ

原题链接

P2197 【模板】Nim 游戏 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

AC代码

#include <iostream>
#include <cstring>
using namespace std;
#define int long long
const int N = 1e7 + 10, mod = 1e9 + 7;
int n, res;
void solve()
{cin >> n, res = 0;for (int i = 0, a; i < n; i++)cin >> a, res ^= a;res ? cout << "Yes\n" : cout << "No\n";
}
signed main()
{ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);//freopen("in.txt", "r", stdin);int _ = 1;cin >> _;while (_--)solve();return 0;
}

1.3.2P1247 取火柴游戏

原题链接

P1247 取火柴游戏 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

AC代码

#include <iostream>
#include <cstring>
using namespace std;
#define int long long
const int N = 5e5 + 10, mod = 1e9 + 7;
int n, res, a[N];
void solve()
{cin >> n, res = 0;for (int i = 0; i < n; i++)cin >> a[i], res ^= a[i];if (!res){cout << "lose";return;}for (int i = 0; i < n; i++){if ((a[i] ^ res) >= a[i])continue;cout << a[i] - (a[i] ^ res) << ' ' << i + 1 << '\n', a[i] = a[i] ^ res;break;}for (int i = 0; i < n; i++)cout << a[i] << ' ';
}
signed main()
{ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);freopen("in.txt", "r", stdin);int _ = 1;// cin >> _;while (_--)solve();return 0;
}

---

二、台阶型Nim游戏

2.1问题描述

有1~n级台阶，第 i 级台阶上摆放ai个石子，每次操作可将第k级台阶上的石子移一些到第k - 1级台阶上，移到第0级台阶(地面)的石子不能再移动。
如果一个人没有石子可以移动，他就输了，问先手是否必胜。

2.2结论及证明

2.2.1结论

必胜态为：奇数级台阶的石子数异或和不为0。必败态为：和必胜态相反

2.2.2结论证明

• 证明：必胜态的后继状态至少存在一个必败态
  • 若A1 ^ A3 ^…… ≠ 0 ，那么必然存在ai(i为奇数)，ai ^ s <= ai，我们操作第i级台阶使其变为ai ^ s
  • 那么后继状态奇数级台阶石子数异或和为0，为必败态
• 证明：必败态的后继状态均为必胜态
  • 由于若A1 ^ A3 ^…… = 0，无论玩家操作奇数级台阶还是偶数级台阶都会使得某一奇数级台阶石子数改变
  • 从而使得A1 ^ A3 ^…… ≠ 0

2.3OJ练习

2.3.1Georgia and Bob

原题链接

1704 – Georgia and Bob (poj.org)

思路分析

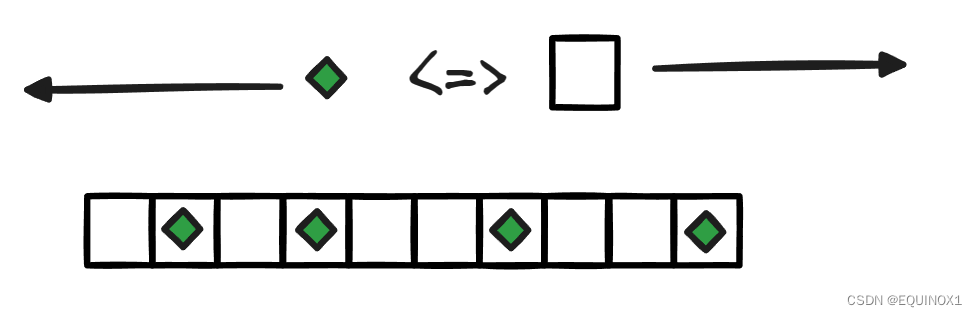
我们发现主席左移等效于空白右移

那么这就转化为了台阶型NIM问题

如上图中有四段连续空白块，相当于四个台阶，需要说明的是，我们只统计最后一个主席左边的空白块，最后一个主席右边相当于地面

那么我们直接按照台阶型NIM来做即可

AC代码

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
#define int long long
const int N = 5e5 + 10, mod = 1e9 + 7;
int n, res, a[N], b[N];
void solve()
{cin >> n, res = 0;for (int i = 1; i <= n; i++)cin >> a[i];sort(a + 1, a + 1 + n);for (int i = n, j = 1; i >= 1; i--)b[j++] = a[i] - a[i - 1] - 1;for (int i = 1; i <= n; i += 2)res ^= b[i];if (res)cout << "Georgia will win\n";elsecout << "Bob will win\n";
}
signed main()
{ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);//freopen("in.txt", "r", stdin);int _ = 1;cin >> _;while (_--)solve();return 0;
}

码蹄集 (matiji.net)

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
#define int long long
typedef pair<int, int> PII;
const int mod = 998244353, inv2 = 499122177;
const int N = 5e5 + 5;
#define lc p << 1
#define rc p << 1 | 1
int n, tot, id[N];
struct data
{int i, x, y;
} datas[N];
struct node
{int l, r;int cnt, s, pw;
} tr[N << 2];
int qp(int a, int b)
{int res = 1;while (b){if (b & 1)res = res * a % mod;b >>= 1, a = a * a % mod;}return res;
}void pushup(int p)
{tr[p].s = (tr[lc].s * tr[rc].pw % mod + tr[rc].s) % mod, tr[p].pw = tr[lc].pw * tr[rc].pw % mod, tr[p].cnt = tr[lc].cnt + tr[rc].cnt;
}
void build(int p, int l, int r)
{tr[p].l = l, tr[p].r = r, tr[p].pw = 1;if (l == r)return;int mid = (l + r) >> 1;build(lc, l, mid), build(rc, mid + 1, r);
}void update(int p, int c, int x)
{if (tr[p].l == tr[p].r){if (!tr[p].cnt)tr[p].s = inv2;tr[p].cnt += x;tr[p].pw = tr[p].pw * qp(inv2, x) % mod;return;}int mid = (tr[p].l + tr[p].r) >> 1;if (c <= mid)update(lc, c, x);elseupdate(rc, c, x);pushup(p);
}
PII query(int p, int l, int r)
{PII res, lp, rp;if (l <= tr[p].l && tr[p].r <= r)return make_pair(tr[p].s, tr[p].pw);int mid = (tr[p].l + tr[p].r) >> 1;if (r <= mid)return query(lc, l, r);if (l > mid)return query(rc, l, r);lp = query(lc, l, r), rp = query(rc, l, r);res.first = (lp.first * rp.second % mod + rp.first) % mod, res.second = lp.second * rp.second % mod;return res;
}
signed main()
{ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);//freopen("in.txt", "r", stdin);cin >> n;for (int i = 0; i < n; i++){cin >> datas[i].i >> datas[i].x >> datas[i].y;if (datas[i].i == 1)id[++tot] = datas[i].x;}sort(id + 1, id + tot + 1);tot = unique(id + 1, id + tot + 1) - id - 1;build(1, 1, tot);for (int i = 0, a, b; i < n; i++){if (datas[i].i == 1)update(1, lower_bound(id + 1, id + tot + 1, datas[i].x) - id, datas[i].y);else{a = lower_bound(id + 1, id + tot + 1, datas[i].x) - id, b = upper_bound(id + 1, id + tot + 1, datas[i].y) - id - 1;cout << (a <= b ? query(1, a, b).first : 0) << '\n';}}return 0;
}

---

三、有向图游戏，SG函数

3.1定义

3.1.1有向图游戏

给定一个有向无环图，图中有唯一一个起点，起点处放有一个棋子，两名玩家交替地把这枚棋子沿有向边进行移动，每次可以移动一步，无法移动者判负。该游戏被称为有向图游戏。

3.1.2Mex运算

设S表示一个非负整数集合。定义Mex(S)为求出不属于集合S的最小非负整数的运算，即：
$$
mex(S) = min{x},x \in N, x \notin S

$$

3.1.3SG函数

在有向图游戏中，对于每个节点x，设从x出发共有k条有向边，分别到达节点y1，y2……yk，定义SG(x)为x的后继节点y1，y2……yk的SG函数值构成的集合再执行mex运算的结果，即：
S G ( x ) = m e x ( { S G ( y 1 ) , S G ( y 2 ) , … … , S G ( y k ) } ) SG(x)=mex(\{SG(y1),SG(y2),……,SG(yk)\}) SG(x)=mex({SG(y1),SG(y2),……,SG(yk)})

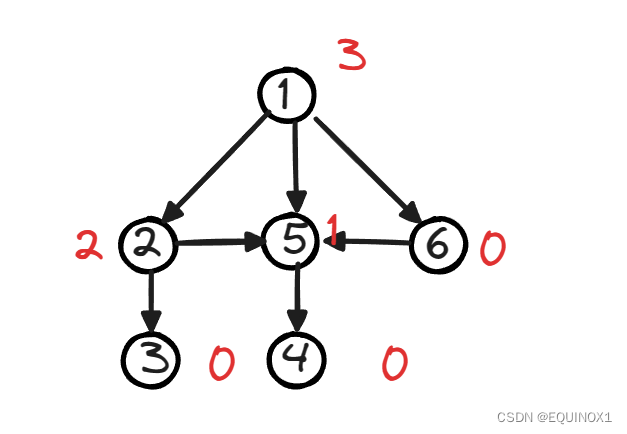
3.1.4有向图游戏的和

设G1，G2，……，Gm是m个有向图游戏。定义有向图游戏G，它的行动规则是任选某个有向图游戏Gi上行动一步。G被称为有向图游戏G1，G2……Gm的和。

有向图游戏的和的SG函数值等于它包含的各个子游戏的SG函数值的异或和，即：
$$SG(x)=SG(y1)\oplus SG(y2),\dots \dots ,\oplus SG(yk)$$

3.2定理及证明

3.2.1定理内容

• 有向图游戏的某个局面必胜，当且仅当该局面对应节点的SG函数值大于0。
• 有向图游戏的某个局面必败，当且仅当该局面对应节点的SG函数值等于0。

3.2.1定理证明

证明思路仍然为证明必胜态必败态交替出现

• 证明：必胜态的后继状态至少存在一个必败态
  • 设SG(y1) ^ SG(y2),……,^SG(yk) = s，设s的最高位为第k位
  • 可以找到第k位为1的SGi，由于Gi = mex({SG(yi)})（yi为i的后继节点）
  • 则SGi必然可以转移到SGi ^ s
• 证明：必败态的后继状态均为必胜态
  • 无论选择哪个有向图游戏进行移动，都会使得新的有向图游戏和的SG函数值异或和不为0
• 证毕

其实对于SG函数可以这样理解：

在一个没有出边的节点上，棋子不能移动，它的SG值为0，对应必败局面。

若一个节点的某个后继节点SG值为0，在mex运算后，该节点的SG值大于0。
这等价于，若一个局面的后继局面中存在必败局面，则当前局面为必胜局面。

若一个节点的后继节点SG值均不为0，在mex运算后，该节点的SG值为0。这
等价于，若一个局面的后继局面全部为必胜局面，则当前局面为必败局面。

3.3有向无环图上的棋子游戏

3.3.1问题描述

给定一个有n个节点和m条边的有向无环图，k个棋子所在的节点编号。

两名玩家交替移动棋子，每次只能将任意一颗棋子沿有向边移到另一个点，无法移动者视为失败。

如果两人都采用最优策略，问先手是否必胜。

3.3.2思路分析

k个棋子都是独立的，我们可以把k个棋子看作k个有向图游戏，先建图然后用SG定理进行判断即可。

3.3.3原题链接

信息学奥赛一本通（C++版）在线评测系统 (ssoier.cn)

3.3.4AC代码

#include <iostream>
#include <algorithm>
#include <unordered_set>
#include <cstring>
using namespace std;
#define int long long
const int N = 2e3 + 10, M = 12010, mod = 1e9 + 7;
struct edge
{int v, nxt;
} edges[M];
int head[N], f[N], idx = 0;
void addedge(int u, int v)
{edges[idx] = {v, head[u]}, head[u] = idx++;
}
int n, m, k, res = 0;
int sg(int x)
{if (~f[x])return f[x];unordered_set<int> s;for (int i = head[x]; ~i; i = edges[i].nxt)s.insert(sg(edges[i].v));for (int i = 0;; i++)if (!s.count(i))return f[x] = i;return -1;
}
void solve()
{memset(head, -1, sizeof head), memset(f, -1, sizeof f);cin >> n >> m >> k;for (int i = 0, a, b; i < m; i++)cin >> a >> b, addedge(a, b);for (int i = 0, x; i < k; i++)cin >> x, res ^= sg(x);res ? cout << "win" : cout << "lose";
}
signed main()
{ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);//freopen("in.txt", "r", stdin);int _ = 1;// cin >> _;while (_--)solve();return 0;
}

3.4 集合型NIM游戏

3.4.1问题描述

给定m个整数组成的集合ai，给定n堆石子的数量bi。

两名玩家轮流操作，每次操作可以从任意一堆石子中拿取石子，每次拿取的石子数目必须是集合a中的整数，最后无法进行操作的人视为失败。

如果两人都采用最优策略，问先手是否必胜。

3.4.2思路分析

每堆石子都是孤立的，把n堆石子看做n个有向图游戏。然后利用SG定理即可。

对于子节点的寻找直接根据集合a内元素进行判断即可，省去了建图。

3.4.3原题链接

Problem - 1536 (hdu.edu.cn)

3.4.4AC代码

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
#define int long long
const int N = 10005, M = 105, mod = 1e9 + 7;
int a[M], f[N], k, m, n;
int sg(int x)
{if (~f[x])return f[x];bool vis[M]{0};for (int i = 0; i < k && x >= a[i]; i++)vis[sg(x - a[i])] = 1;for (int i = 0;; i++)if (!vis[i])return f[x] = i;return -1;
}
void solve()
{while (cin >> k, k){memset(f, -1, sizeof f);for (int i = 0; i < k; i++)cin >> a[i];sort(a, a + k), cin >> m;while (m--){cin >> n;int res = 0;for (int i = 0, x; i < n; i++)cin >> x, res ^= sg(x);res ? cout << 'W' : cout << 'L';}cout << '\n';}
}
signed main()
{ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);//freopen("in.txt", "r", stdin);int _ = 1;while (_--)solve();return 0;
}

3.5普通NIM游戏与有向图游戏的关系

将一个有x个石子的堆视为节点x，当y < x时，节点x可以到y。
由n个堆组成的Nim游戏，可以视为n个有向图游戏。
而显然对于有x个石子的堆显然可以抵达0~x-1的所有堆，那么其sg值就是x

于是我们就可以省去sg的计算，直接由每堆石子数目的异或和来得到答案。

3.6OJ练习-POJCutting Game

3.6.1原题链接

2311 – Cutting Game (poj.org)

3.6.2思路分析

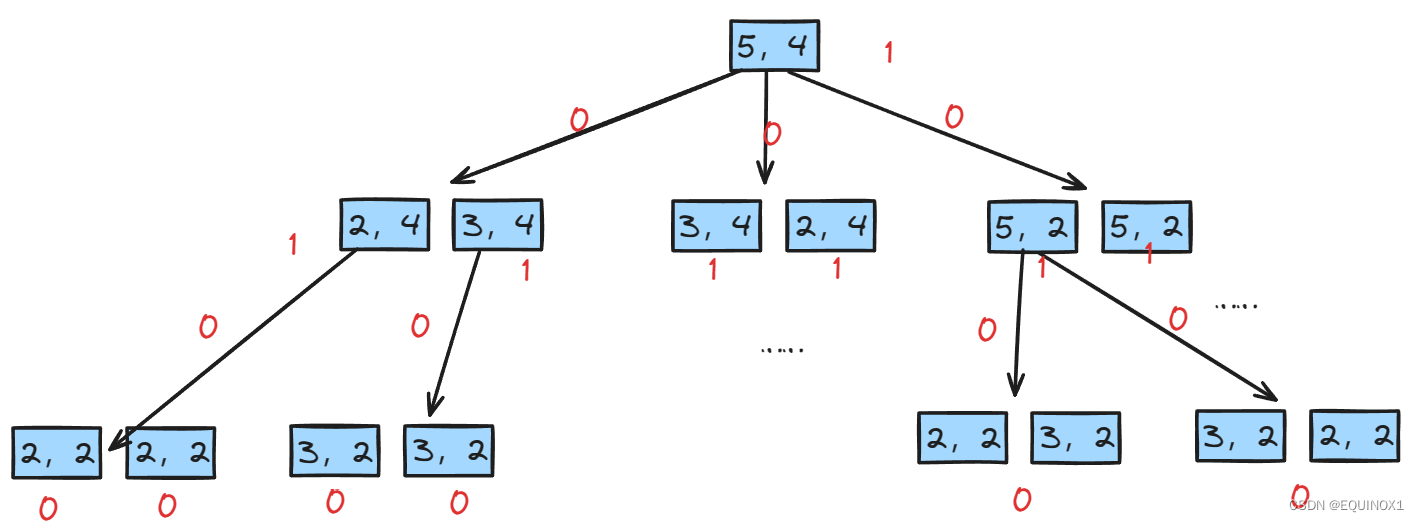
我们自底向上思考

如果当前状态为1 * x或者x * 1，那么该玩家必胜

向上推一层，对于2*3、3*2和2*2三个状态，无论怎么剪都会剪出来一个必胜态，于是2 * 3、3 * 2和2 * 2就是必败态

不失一般性地考虑，对于m*n，只考虑2……m-2 * n和m * 2……n-2的后继状态，那么剪一次会有两个子节点，它们两个不互相独立

也就是说，我们要把两个子节点看成一个组合状态，其sg值为s(y1) ^ s(y2)（y1y2对应某种裁剪策略产生的两个子节点）

然后我们就可以跑sg了，根据根节点的sg值输出即可

3.6.3AC代码

#include <iostream>
#include <algorithm>
#include <cstring>
#include <set>
using namespace std;
const int N = 210, mod = 1e9 + 7;
int m, n, f[N][N];
int sg(int x, int y)
{if (~f[x][y])return f[x][y];set<int> s;for (int i = 2; i <= x - 2; i++)s.insert(sg(i, y) ^ sg(x - i, y));for (int i = 2; i <= y - 2; i++)s.insert(sg(x, i) ^ sg(x, y - i));for (int i = 0;; i++)if (!s.count(i))return f[x][y] = f[y][x] = i;return -1;
}
void solve()
{memset(f, -1, sizeof f);while (cin >> m >> n){sg(m, n) ? cout << "WIN\n" : cout << "LOSE\n";}
}
signed main()
{ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);//freopen("in.txt", "r", stdin);int _ = 1;while (_--)solve();return 0;
}