1. 频率域采样
(1) 采样的过程:DFT的X(k)是对周期且连续的频谱X()在[0,2pi)上的等间隔采样,采N个点得到的,采样间隔是
;频域采样要求时域有限,即假设x(n)的长度是有限值M,x(n)的SFT是X(
)。
(2) X(k) 做IDFT之后得到的和原序列x(n)长度都是N个点,在数值上有何关系?
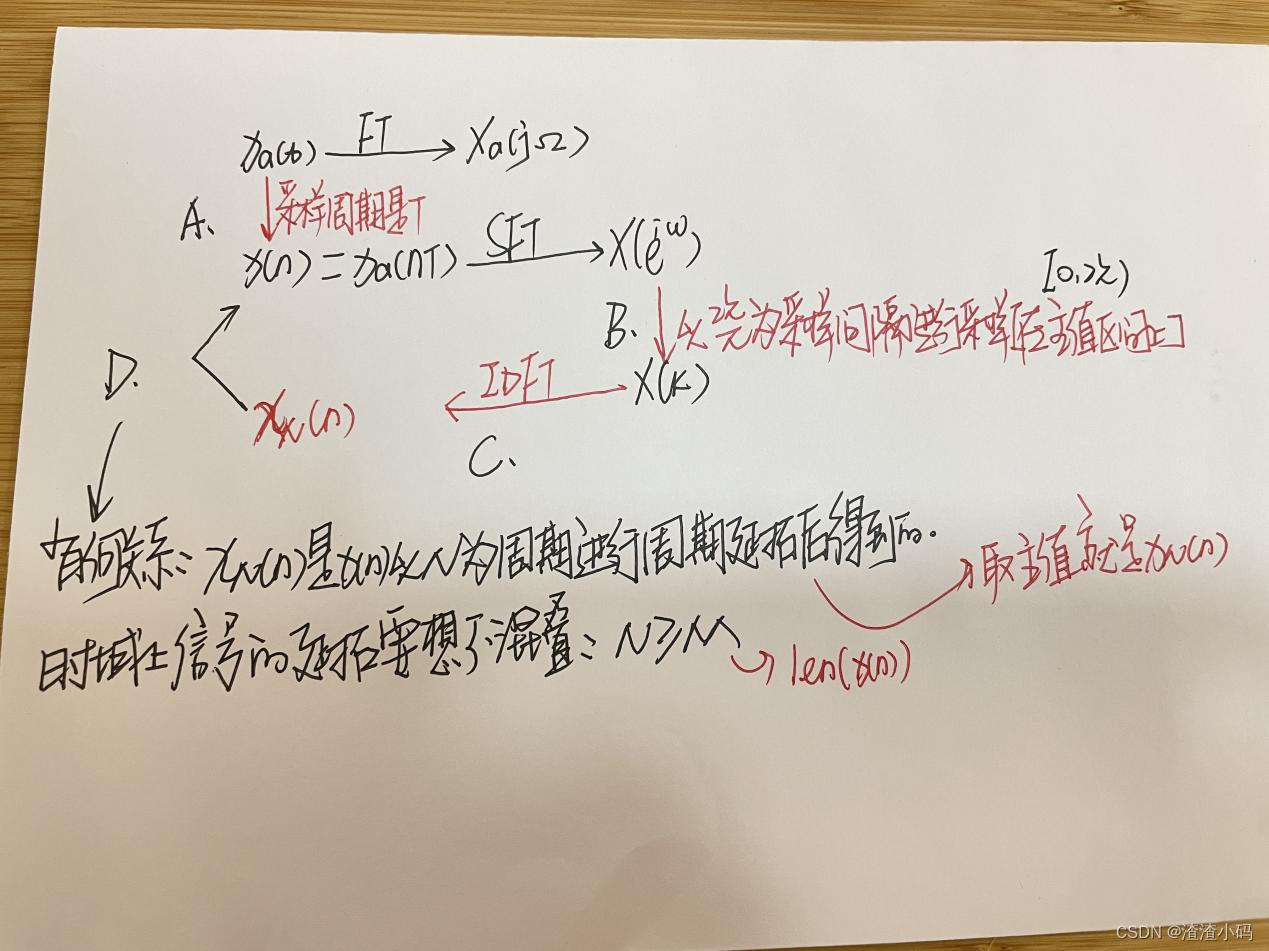
2. 示例
示例1
已知某一序列为x(n)≠0, 0≤n≤19,其SFT为X(),对其SFT分别以N=32和N=16点采样,观察采样后逆变换的时域信号原时域信号的关系,时域信号对应的频谱和原时域信号频谱的关系。
代码:
%Fs=256;%采样率%N=256; %采样点数%n=0:N-1;%采样序列%t=0:1/Fs:1-1/Fs;%时间序列%x=2+3*cos(2*pi*50*t-pi*30/180)+1.5*cos(2*pi*75*t-pi*90/180);%原始信号%原始信号有直流分量,%频率分量1:模拟频率是50Hz, 相位是1/6*pi(rad)-->对应30度的角度制,幅度是3%频率分量2:模拟频率是75Hz, 相位是1/2*pi(rad)-->对应90度的角度制,幅度是1.5%y=fft(x);%对原始信号做FFT%M=abs(y);%求复频域上的模值%plot(n, M);%绘制幅度谱曲线%xlabel('n');clear;%清除内存close all;%关闭所有图形x=[1 2 3 4 5 6 7 8 9 10 10 9 8 7 6 5 4 3 2 1];%产生信号xf=fft(x,2048);%求信号的近似SFTy1f=xf(1:64:2048); %在SFT上采样32点y2f=xf(1:128:2048); %在SFT上采样16点y1=ifft(y1f);%求y1(n)y1sft=fft(y1,2048);%求32点采样后的SFTy2=ifft(y2f);%求y2(n)y2sft=fft(y2,2048);%求16点采样后的SFTfigure;subplot(3,1,1);stem(0:19,x);%绘制离散序列数据grid on;%显示网格线xlabel('n','fontsize',12);ylabel('x(n)','fontsize',12);title('原序列(时域)','fontsize',12);subplot(3,1,2);plot((0:2047)/1024, abs(xf));%绘制二维曲线grid on;hold on;%保留当前绘图(接下来要绘制新的绘图[叠加到上面的二维曲线])stem((0:64:2047)/1024,abs(y1f),'r');ylim([0 110]);%设置y轴坐标范围xlabel('\omega/\pi','fontsize',14);ylabel('幅度(dB)','fontsize',12);xlim([0 2048/1024]);title('对SFT的32点采样(频域采样)','fontsize',12);subplot(3,1,3),%画频域上采32个点对应的时域图stem(0:31,y1);grid on;ylim([0 10]);xlabel('n','fontsize',12);ylabel('y1(n)','fontsize',12);title('频域上采32个点对应的时域离散序列','fontsize',12);figure;%绘制新图形subplot(3,1,1);stem(0:19,x);grid on;xlabel('n','fontsize',14);ylabel('x(n)','fontsize',14);title('原序列(时域)','fontsize',12);subplot(3,1,2),plot((0:2047)/1024,abs(xf));grid on;hold on;stem((0:128:2047)/1024,abs(y2f),'r');ylim([0 110]);xlabel('\omega/\pi','fontsize',14);ylabel('幅度(dB)','fontsize',14);xlim([0 2048/1024]);title('对SFT的16点采样(频域采样)','fontsize',14);subplot(3,1,3);stem(0:15,y2);grid on;xlabel('n','fontsize',14);ylabel('y2(n)','fontsize',14);title('频域上采16个点对应的时域离散序列','fontsize',12);figure;plot((0:2047)/1024,abs(xf),'red');%原序列2048点曲线(频域)grid on;hold on;stem((0:128:2047)/1024,abs(y2f),'black');ylim([0 110]);xlim([0 2048/1024]);xlabel('\omega/\pi','fontsize',14);ylabel('幅度(dB)','fontsize',14);title('不同采样点对应的SFT','fontsize',14);legend('原序列SFT','16点采样');figure;plot((0:2047)/1024,abs(xf),'red');%原序列2048点曲线(频域)grid on;hold on;stem((0:64:2047)/1024,abs(y1f),'blue');ylim([0 110]);xlim([0 2048/1024]);xlabel('\omega/\pi','fontsize',14);ylabel('幅度(dB)','fontsize',14);title('不同采样点对应的SFT','fontsize',14);legend('原序列SFT','32点采样');运行结果如下:

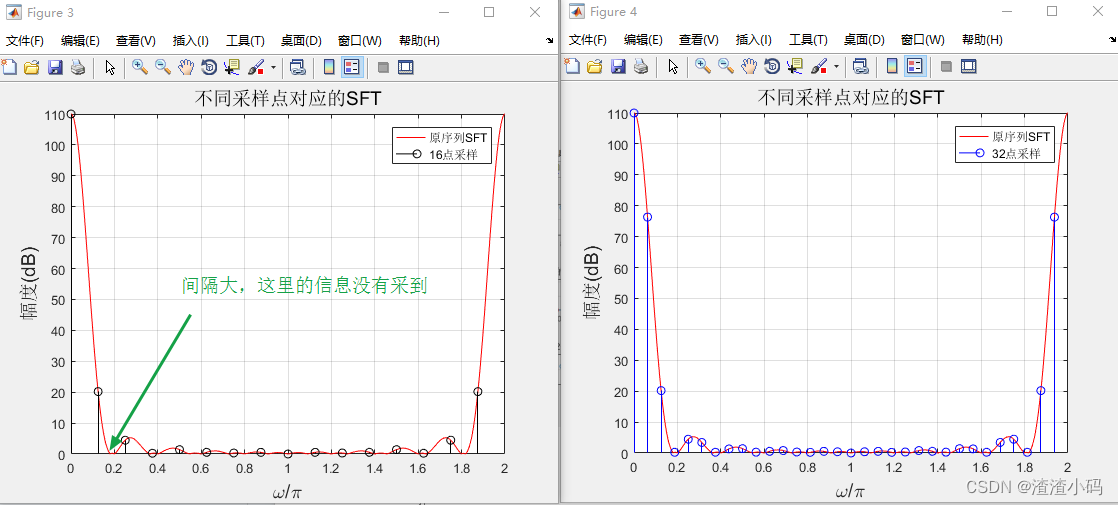
简要分析和对比:
(1) 第一组:当N小于M时,周期延拓后,序列会有重叠
(2) 第二组:采样间隔是,N越小,间隔越大,就采不到原序列的频谱上某些信息点
示例2