leetcode hot 100
- 双指针
- 1.三数之和
- 2.接雨水
- 多维动态规划
- 1.最长公共子序列
双指针
1.三数之和
三数之和
排序 + 双指针的方法,固定一个数nums[i], 用两数和找target -= nums[i] 的数需要注意两点:
1.需要去掉重复数字
while (l < r && nums[l] == nums[--l]);
while (l < r && nums[r] == nums[++r]);
....
while (i < n - 1 && nums[i] == nums[i + 1]) i++;
2.如果用这种方法去掉重复数字,那么一定要先执行 l++ && r–再去执行去重,防止有不重复数字死循环的情况发生
l++, r--;
while (l < r && nums[l] == nums[l - 1]) l++;
while (l < r && nums[r] == nums[r + 1]) r--;
class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums) {sort(nums.begin(), nums.end());int n = nums.size();vector<vector<int>> ans;for (int i = 0; i < n; i++) {int l = i + 1, r = n - 1;int tmptar = -nums[i];while (l < r) {if (nums[l] + nums[r] < tmptar) {l++;} else if (nums[l] + nums[r] > tmptar) {r--;} else {ans.push_back({nums[i], nums[l], nums[r]});l++, r--;while (l < r && nums[l] == nums[l - 1]) l++;while (l < r && nums[r] == nums[r + 1]) r--;}}while (i < n - 1 && nums[i] == nums[i + 1]) i++;}return ans;}
};
2.接雨水
接雨水
- 图1位置的水位由2,3位置决定
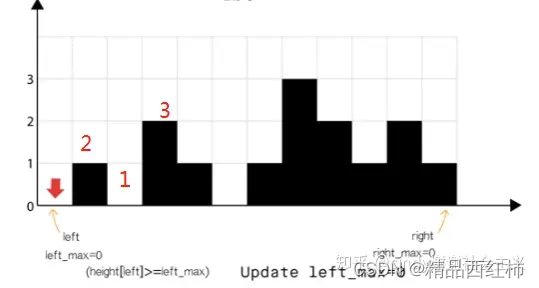
- 双指针相向寻找,需要找到当前遍历过的、左右两侧的最大高度l_max, r_max
- 如果 l_max 小于 r_max,那么左侧一定能够积水,如果 l_max 大于 r_max,右侧一定能够积水
- 左侧,只有当前的高度height[l] < l_max时才能够有积水,否则例如 [0,1,2,3,4,5]是没办法形成积水的
- 同理,右侧,只有当前的高度height[r] < r_max时才能够有积水
class Solution {
public:int trap(vector<int>& height) {int n = height.size();int l = 0, r = n - 1, l_max = 0, r_max = 0, ans = 0;while (l <= r) {if (l_max < r_max) {l_max = max(l_max, height[l]);if (l_max > height[l]) {ans += l_max - height[l];}l++; } else {r_max = max(r_max, height[r]);if (r_max > height[r]) {ans += r_max - height[r];}r--;}}return ans;}
};
多维动态规划
1.最长公共子序列
1)确定状态:对于两个字符串的动态规划问题,套路是通用的。
比如说对于字符串 s1 和 s2,它们的长度分别是 m、n,一般来说都要构造一个这样的 DP table:dp[m + 1][n + 1]
2)转移方程:对于 text1:abcde 和 text2:ace 两个字符串,我们定义两个指针进行遍历 i 和 j。
遍历 text1 长度为 m,定义指针 i,从 0~m。固定 i 指针(i == 1)位置,接下来开始遍历 text2 长度为 n,定义指针 j,从 0~n。
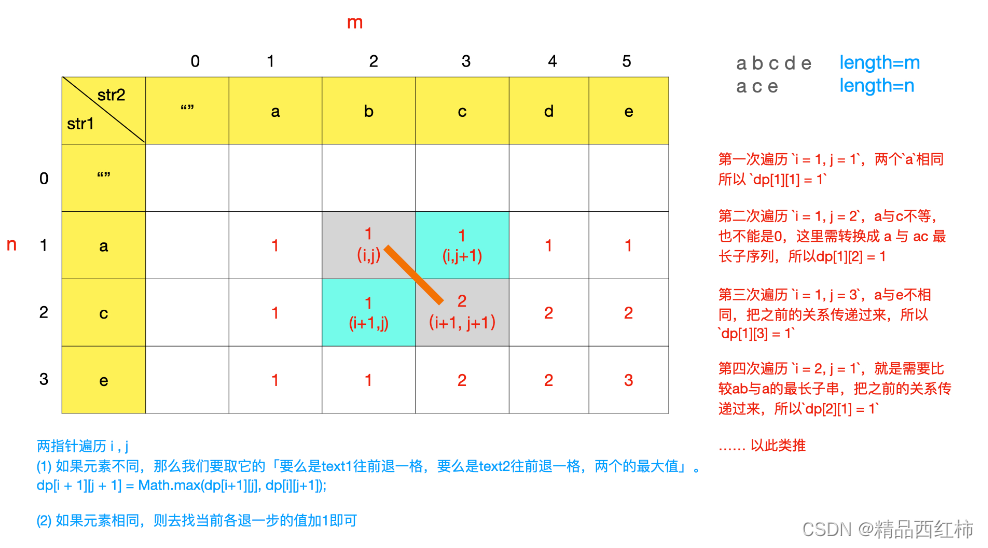
第一次遍历 i = 1, j = 1,两个a相同所以 dp[1][1] = 1
第二次遍历 i = 1, j = 2,a与c不等,也不能是0,这里需转换成 a 与 ac 最长子序列,这里需要把之前的关系传递过来,所以dp[1][2] = 1
第三次遍历 i = 1, j = 3,a与e不相同,把之前的关系传递过来,所以dp[1][3] = 1
text2:ace 已经走完来第一轮,接下来text1:abcde 走到来b字符。
第四次遍历 i = 2, j = 1,就是需要比较ab与a的最长子串,把之前的关系传递过来,所以dp[2][1] = 1
我们会发现遍历两个串字符,当不同时需要考虑两层遍历前面的值(关系传递),也就是左边和上边的其中较大的值,当相同时,需要考虑各自不包含当前字符串的子序列长度,再加上1。
因此可以得出:
现在对比的这两个字符不相同的,那么我们要取它的「要么是text1往前退一格,要么是text2往前退一格,两个的最大值」
dp[i + 1][j + 1] = max(dp[i+1][j], dp[i][j+1]);
对比的两个字符相同,去找它们前面各退一格的值加1即可:dp[i+1][j+1] = dp[i][j] + 1;
3)边界条件:dp[0][X] = 0, dp[X][0] = 0;
4)计算顺序:先行后列
class Solution {
public:int longestCommonSubsequence(string text1, string text2) {int n = text1.size(), m = text2.size();vector<vector<int>> dp(n + 1, vector<int>(m + 1, 0));for (int i = 1; i < n + 1; i++) {for (int j = 1; j < m + 1; j++)if (text1[i - 1] == text2[j - 1])dp[i][j] = dp[i - 1][j - 1] + 1;else dp[i][j] = max(dp[i - 1][j], dp[i][j -1]);}return dp[n][m];}
};