P1255 数楼梯 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
//不满分做法:没有高精度
#include <bits/stdc++.h>
using namespace std;
const int N=5006;
int dp[N];//dp[i]表示到第i节楼梯有dp[i]中方案
int main(){int n;cin>>n;dp[1]=1;dp[0]=1;for(int i=2;i<=n;i++){dp[i]=dp[i-1]+dp[i-2];
//到第i节楼梯的方案数等于到第i-1节楼梯的方案数+第i-2节楼梯的方案数
//第i节楼梯 可与从第i-1节楼梯或者第i-2节楼梯转移过来}cout<<dp[n];return 0;
}P1002 [NOIP2002 普及组] 过河卒 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
//40分做法 暴力搜索
#include<bits/stdc++.h>
using namespace std;
long long n,m,cx,cy;
int fx[]={2,-2,1,-1,2,-2,1,-1};
int fy[]={1,-1,-2,2,-1,1,2,-2};//马的控制点
int mp[30][30];
int xx[]={1,0};//往下和往右
int yy[]={0,1};
int ans=0;//方案数
void dfs(int x,int y){if(x==n&&y==m){ans++;return ;}for(int i=0;i<2;i++){if(x+xx[i]>n||y+yy[i]>m)continue;//不越界if(mp[x+xx[i]][y+yy[i]]!=-1)dfs(x+xx[i],y+yy[i]);}return ;
}
int main(){cin>>n>>m>>cx>>cy;//输入地图的大小和马的坐标mp[cx][cy]=-1;//马的位置不能走for(int i=0;i<8;i++)mp[cx+fx[i]][cy+fy[i]]=-1;//马的控制点不能走dfs(0,0);//从(0,0)开始搜cout<<ans;return 0;
}
#include<bits/stdc++.h>
using namespace std;
const int dir[8][2]={{1,2},{1,-2},{2,1},{2,-1},{-1,2},{-1,-2},{-2,1},{-2,-1}};//八个方向控制点
bool d[30][30];//地图的大小
long long dp[30][30],n,m,cx,cy;//dp[i][j]表示到达(i,j)的方案数
int main(){cin>>n>>m>>cx>>cy;d[cx][cy]=true;//马的位置设为true 不能走for(int i=0;i<8;i++){int tx=cx+dir[i][0],ty=cy+dir[i][1];if(tx>=0&&tx<=n&&ty>=0&&ty<=m) d[tx][ty]=true;//控制点的位置合法且不越界 设为true}dp[0][0]=1;//到达(0,0)只有一种方法for(int i=0;i<=n;i++){for(int j=0;j<=m;j++){if(d[i][j]==false){//如果不是马的控制点说明能走if(i) dp[i][j]+=dp[i-1][j];//dp[i-1][j]不出界if(j) dp[i][j]+=dp[i][j-1];//dp[i][j-1]不出界//假设马的位置在两个地图的边界 那他的控制点就有可能出界这是不合法的}}}cout<<dp[n][m]<<'\n';return 0;
}P1044 [NOIP2003 普及组] 栈 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
P1028 [NOIP2001 普及组] 数的计算 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
//暴力枚举 超时递归
#include<cstdio>
using namespace std;
int n,cnt=1;
void func(int x){for(int i=1;i<=x/2;i++){cnt++;func(i);}
}
//6 (1)
//6 1(2)
//6 2 (3)
//6 2 1(4)
//6 3(5)
//6 3 1(6)int main(){scanf("%d",&n);func(n);printf("%d\n",cnt);
}#include <bits/stdc++.h>
using namespace std;
const int N=1e4+6;
int sum=1;
int f[N];//dp[i]表示以数字i或小于等于i为结尾的数的方案数
int main(){int n;cin>>n;for(int i=1;i<=n;i++){for(int j=1;j<=i/2;j++){f[i]+=f[j];}f[i]++;//自身算一种}cout<<f[n];return 0;
}
P1928 外星密码 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
P1464 Function - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
#include <cstdio>
#define LL long long
LL dp[25][25][25];
LL w(LL a, LL b, LL c){if(a <= 0 || b <= 0 || c <= 0) return 1;//两个特判,题意里都有的。if(a > 20 || b > 20 || c > 20) return w(20, 20, 20);if(a <b && b < c)//情况一,每一个没有储存过的“w”值全部储存,如果有就直接调用。{if(dp[a][b][c-1] == 0){dp[a][b][c-1] = w(a, b, c-1);}if(dp[a][b-1][c-1] == 0){dp[a][b-1][c-1] = w(a, b-1 ,c-1);}if(dp[a][b-1][c] == 0){dp[a][b-1][c] = w(a, b-1, c);}dp[a][b][c] = dp[a][b][c-1] + dp[a][b-1][c-1] - dp[a][b-1][c];}else//同上{if(dp[a-1][b][c] == 0){dp[a-1][b][c] = w(a-1, b, c);}if(dp[a-1][b-1][c] == 0){dp[a-1][b-1][c] = w(a-1, b-1 ,c);}if(dp[a-1][b][c-1] == 0){dp[a-1][b][c-1] = w(a-1, b, c-1);}if(dp[a-1][b-1][c-1] == 0){dp[a-1][b-1][c-1] = w(a-1, b-1, c-1);}dp[a][b][c] = dp[a-1][b][c] + dp[a-1][b][c-1] + dp[a-1][b-1][c] - dp[a-1][b-1][c-1];}return dp[a][b][c];
}int main()
{LL a, b, c;while(scanf("%lld%lld%lld", &a, &b, &c))//无限输入,直到“-1 -1 -1”{if(a == -1 && b == -1 && c == -1) return 0;//-1 -1 -1就直接结束,不运算了。printf("w(%lld, %lld, %lld) = ", a, b, c);printf("%lld\n", w(a, b, c));}
}P2437 蜜蜂路线 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
//没有高精度
#include <bits/stdc++.h>
#define int long long
using namespace std;
int n,m;
int ans=0;
const int N=1e5+6;
int dp[N];//dp[i表示走到第i个格子的方案数
signed main(){cin>>n>>m;dp[n]=1;dp[n+1]=1;for(int i=n+2;i<=m;i++){dp[i]=dp[i-1]+dp[i-2];}cout<<dp[m];return 0;
}P1164 小A点菜 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
#include <bits/stdc++.h>
using namespace std;
const int N=1e4+6;
int cnt=0;
int n,m;
int a[N];
int dp[N];//dp[i]表示在只选择前面几种商品的条件下花费为i的方案数
int main(){cin>>n>>m;for(int i=1;i<=n;++i){cin>>a[i];}dp[0]=1;for(int i=1;i<=n;i++){for(int j=m;j>=a[i];j--){dp[j]=dp[j-a[i]]+dp[j];//选和不选两种情况转移过来}}cout<<dp[m];return 0;
}P1036 [NOIP2002 普及组] 选数 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
#include <bits/stdc++.h>
using namespace std;
int n,k;
const int N=26;
int a[N],vis[N]={0};
int ans=0;
typedef long long ll;
bool isprime(int x){for(int i=2;i*i<=x;i++){if(x%i==0)return 0;}return 1;
}
void dfs(int m, int sum, int startx){//最重要的递归
//m代表现在选择了多少个数
//sum表示当前的和
//startx表示升序排列,以免算重
// 比如数有 123 没有startx可以选出12 21 而有的话不会再往前面找了if(m == k){//如果选完了的话if(isprime(sum))ans++;//ans加一return ;}for(int i = startx; i < n; i++)//往后找dfs(m + 1, sum + a[i], i + 1);//递归//步数要加一,和也要加//升序起始值要变成i+1,以免算重return ;//这一个步骤下,所有的都枚举完了//直接返回去
}
int main(){scanf("%d%d",&n,&k);//输入for(int i = 0; i < n; i++)scanf("%d",&a[i]);//循环读入dfs(0,0,0);//调用函数printf("%d\n",ans);//输出答案return 0;//结束程序
}
//另一种思路错的原因是因为可能出现 1 2 1 1 3 6 7这样的情况P1990 覆盖墙壁 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
这道题其实就是一道递推题目,但它的递推公式又很复杂。
不得不说,前面两位DALAO的解法都是对的,但他们没有讲到他们写的状态转移方程是怎么来的,所以这应该会让很多蒟蒻(包括笔者本人)一脸懵逼~~~。所以本人打算详细地讲一讲这一题。
下面开始进入题解:
首先,既然是递推,那么分好状态就是一件非常重要的事情。这里本人直接讲状态。
(下文中的F[N]表示铺满前N*2的面积的墙的方案数;“一列”指长为1,宽为2的墙壁)
1.当这面墙的最后一列被铺满时(如下图所示)
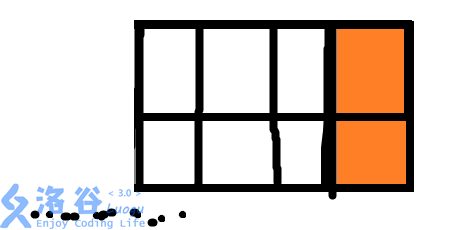
以这种状态结尾的方案数为F[N-1]。
2.当这面墙的最后两列被铺满时(如下图所示,注意颜色的区别)

以这种状态结尾的方案数为F[N-2]。
大家也看到,前两种状态很容易想到,也很容易描述。
但是,L形的瓷砖又怎么办呢?
(呵呵,刚开始想到这里的时候,我自己都蒙了。)
为了方便大家思考,我们先往简单的方向想。(以下是重点!!!)
我们可以用一个数组G[N]来表示**铺满前(N+1)*2的面积的墙,但是第(N+1)列有一个瓷砖已经被铺过(注意,是已经被铺过!)**的方案数。
所以,L形瓷砖的问题就已经被“初步”解决了。
所以,下面这种情况的方案数就是G[N-2](因为实际上第N列已经铺满了,所以这里要处理的是前N-1列墙,所以多减了1)(如下图所示):
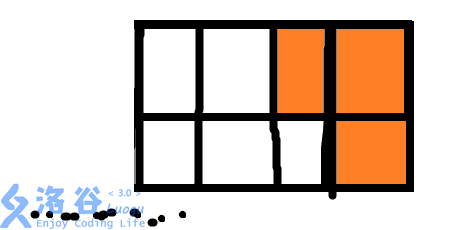
同理,这一种情况的方案数也是G[N-2]:
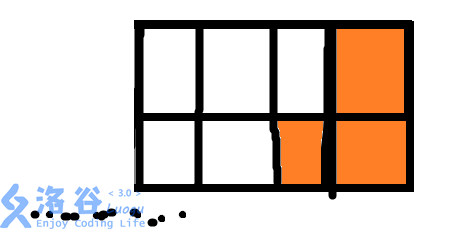
OK,现在问题来了:这个G数组应该怎么维护呢?
不急,我们可以画图。
首先,第一种情况就是直接先让它变成一个长方形:
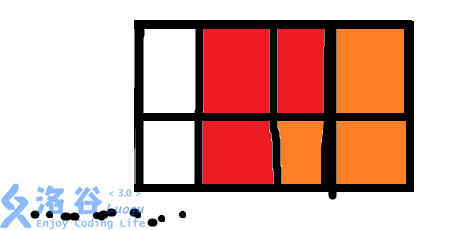
以这种状态结尾的方案数为F[N-3]。
第二种情况是,加上一块砖后,它仍然不是一个长方形:
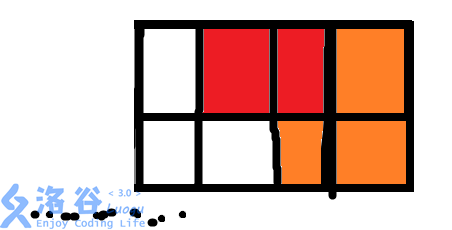
so,这第二种情况的方案数就是G[N-3](可能需要转一下弯,希望大家能弄懂)。
所以,G[N-2](注意,不是G[N])的方案数就等于F[N-3]+G[N-3]。
稍微化简一下,就可以得出:G[N]=F[N-1]+G[N-1]。
所以,F[N]的转移方程就是:
F[N]=F[N-1]+F[N-2]+2*G[N-2](别忘了前面讲过G[N-2]的情况有两种)
而G[N]的转移方程就是:G[N]=F[N-1]+G[N-1]。
初始化:F[0]=1,G[0]=0;F[1]=G[1]=1;
#include<iostream>
using namespace std;const int maxn=1000002;
const int mod=10000;int f[maxn],g[maxn];
//f[i]表示正常铺满的情况下 到第i排时的方案数
//g[i]表示前i排全部铺满 第i+1排只铺一块的方案数
int main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int n;cin>>n;f[0]=1; //g[0]=0f[1]=g[1]=1;for(int i=2;i<=n;i++){f[i]=((f[i-1]+f[i-2])%mod+2*g[i-2]%mod)%mod;g[i]=(g[i-1]+f[i-1])%mod;}cout<<f[n];return 0;
}
//首先f[i]可以从f[i-1]和f[i-2]转移过来
//也可从g[i-2]转移过来 就是铺上一个L形的
//g[i-2]=f[n-3]+g[n-3]
P3612 [USACO17JAN] Secret Cow Code S - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
//暴力写法
#include <bits/stdc++.h>
#define int long long
using namespace std;
signed main() {string str;cin >> str;int n;cin >> n;// 循环直到字符串长度大于等于n+1while (str.length() <= n+1) {// 将字符串str的最后一个字符接在字符串开头char temp = str[str.length() - 1];str += temp + str;}// 输出第n个字符cout << str[n] <<'\n';return 0;
}
//strlen用于char s[]
//str.length()用于string sP1259 黑白棋子的移动 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
P1010 [NOIP1998 普及组] 幂次方 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
P1228 地毯填补问题 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
P1498 南蛮图腾 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
![[C++]AVL树怎么转](https://img-blog.csdnimg.cn/direct/1dc15693bc134af68195cfa67540e4c3.png#pic_center)