704.二分查找

方法一：二分查找

这题就是二分查找的模板题，将二分的模板背上就行了

class Solution {public int search(int[] nums, int target) {int left = 0, right = nums.length - 1;while (left <= right) {int mid = left + right >> 1;if (nums[mid] == target) return mid;else if (nums[mid] > target) right = mid - 1;else if (nums[mid] < target) left = mid + 1;}return -1;}
}

时间复杂度： O(n)
空间复杂度： O(1)

35.搜索插入位置

方法一：二分查找

二分查找 target 的位置，要明确什么时候返回 target 的位置，返回 left 或者是 right - 1

class Solution {public int searchInsert(int[] nums, int target) {int left = 0, right = nums.length - 1;int mid = 0;while (left <= right) {mid = left + right >> 1;if (nums[mid] == target) return mid;else if (nums[mid] > target) right = mid - 1;else if (nums[mid] < target) left = mid + 1;}// return left;return right - 1;}
}

时间复杂度： O(logn)
二分查找的时间复杂度是 O(logn) 级别的

空间复杂度： O(1)

34.在排序数组中查找元素的第一个和最后一个位置

方法一：二分查找

第一次二分查找 nums[mid] >= target 的左边界，第二次二分查找 nums[mid] <= target 的右边界

y总模板

class Solution {public int[] searchRange(int[] nums, int target) {if (nums.length == 0) return new int[]{-1, -1};int l = 0, r = nums.length - 1;while (l < r) {int mid = l + r >> 1;if (nums[mid] >= target) r = mid;else l = mid + 1;}if (nums[r] != target) return new int[]{-1, -1};int L = r;l = 0; r = nums.length - 1;while (l < r) {int mid = l + r + 1 >> 1;if (nums[mid] <= target) l = mid;else r = mid - 1;}return new int[]{L, r};}
}

代码随想录

class Solution {public int[] searchRange(int[] nums, int target) {if (nums.length == 0) return new int[]{-1, -1};int l = 0, r = nums.length - 1;int L = -1, R = -1;while (l <= r) {int mid = l + r >> 1;if (nums[mid] >= target) {L = mid;r = mid - 1;} else {l = mid + 1;}}if (L < 0 || L >= nums.length || nums[L] != target) return new int[]{-1, -1};l = 0; r = nums.length - 1;while (l <= r) {int mid = l + r >> 1;if (nums[mid] <= target) {R = mid;l = mid + 1;} else {r = mid - 1;}}return new int[]{L, R};}
}

时间复杂度： O(logn)
二分查找的时间复杂度是 O(logn) 级别的

空间复杂度： O(1)

69.x的平方根

方法一：袖珍计算器

使用指数函数 exp 和对数函数 log 来代替平方根函数

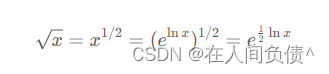
class Solution {public int mySqrt(int x) {if (x == 0) return 0;int ans = (int)Math.exp(0.5 * Math.log(x));return (long)(ans + 1) * (ans + 1) <= x ? ans + 1 : ans;}
}

时间复杂度： O(1)

空间复杂度： O(1)

方法二：二分查找

由于 x 平方根的整数部分 ans 是满足 k²≤x 的最大 k 值，因此我们可以对 k 进行二分查找，从而得到答案。

class Solution {public int mySqrt(int x) {int left = 0, right = x;int mid = 0, ans = -1;while (left <= right) {mid = left + right >> 1;if (mid * mid <= x) {left = mid + 1;ans = mid;}else right = mid - 1;}return ans;}
}

时间复杂度： O(logn)
二分查找的时间复杂度是 O(logn) 级别的

空间复杂度： O(1)

方法三：牛顿迭代法

没看懂。。。。
后面懂了再更新

367.有效的完全平方数

方法一：使用内置函数

class Solution {public boolean isPerfectSquare(int num) {int x = (int) Math.sqrt(num);return x * x == num;}
}

方法二：暴力

从 1 开始遍历，如果出现了 x * x > num 的情况，说明后面的数也不可能满足情况了，就结束遍历即可

class Solution {public boolean isPerfectSquare(int num) {long x = 1, square = 1;while (square <= num) {if (square == num) return true;x ++ ;square = x * x;}return false;}
}

时间复杂度： O(√n)
n 为 num 的最大值，最多只需遍历 √n + 1 个值

空间复杂度： O(1)

方法三：二分查找

与上个题目的二分查找类似

class Solution {public boolean isPerfectSquare(int num) {int l = 0, r = num;int ans = -1;while (l <= r) {int mid = l + r >> 1;long square = (long) mid * mid;if (square == num) return true;else if (square < num) l = mid + 1;else r = mid - 1;}return false;}
}

方法四：牛顿迭代法

看不懂。。。
但是看答案，与上个题目的牛顿迭代法答案类似，或许直接背一个模板也可以吧。哈哈哈哈哈哈。。。