本节复习快速排序， 快排我们要讲三个版本：一种是霍尔大佬的原版版本， 也就是快速排序的原版。 一种挖坑法。还有一种前后指针法。 

首先我们应该知道，三个版本针对的是单趟进行排序的方法不同。 而多趟使用的是递归或者非递归模拟二叉树。 是的， 快排分为递归版本和非递归版本。 两种版本的实现方法本节都会详细实现。 由于单趟是一样的， 我们先来分析单趟的方法。

目录

单趟排序

霍尔版本

 挖坑法

前后指针法

多趟排序

递归

 非递归

---

单趟排序

霍尔版本

快排的三个版本的单趟的函数中， 都要传送进行排序的区间。 不用传送排序的数据个数。就像这样：

void partSort1(int* arr, int left, int right)//arr是要排序的数组， left是左闭区间， right是右闭区间
{//……内容
}

然后， 我们来看一下具体的实现过程：、

假设有这么一串数组：a[10] = { 6, 0, 7, 5, 4, 3, 1, 2, 8, 9 }。要对这个数组进行排序， 那么单趟过程如下：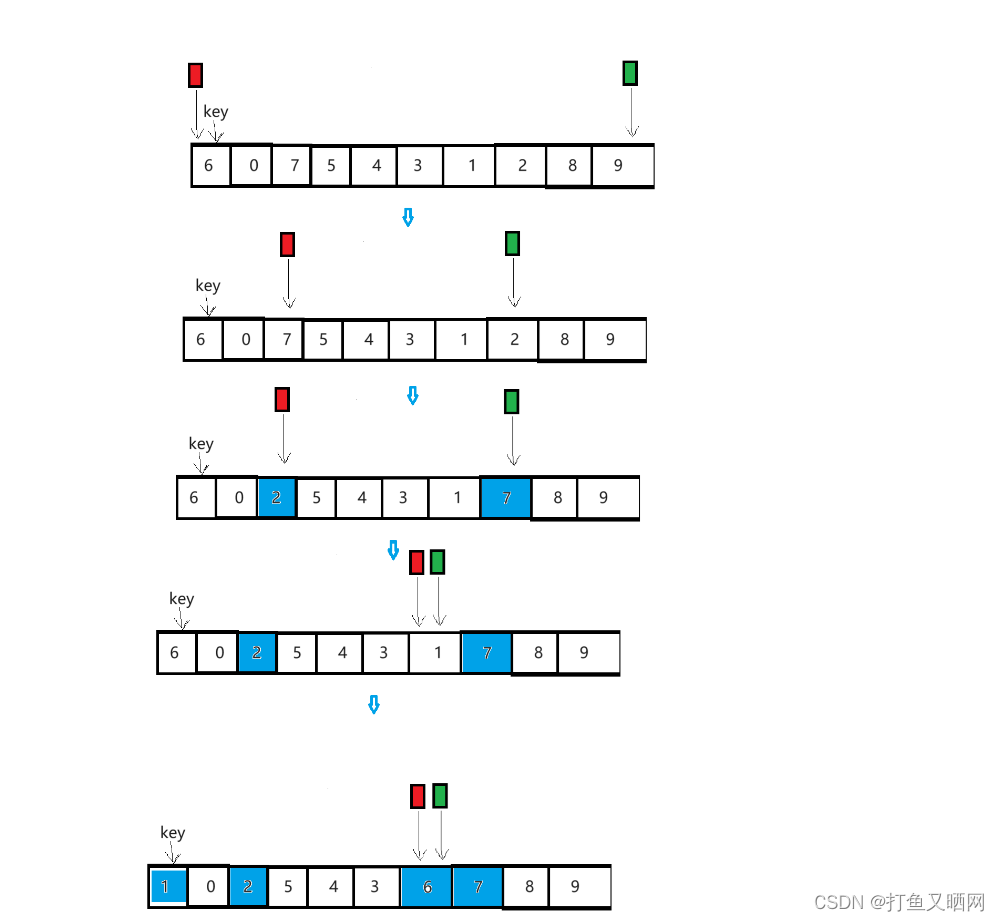

具体过程是这样的:left就代表着红指针， right就代表着绿指针。

然后还有一个keyi指针指向left的初始位置， 也就是最左边（这里不是必须指向最左边。 也可以指向最右边。 不过指向的初始位置决定着过程的走向， 这里以最左边演示）。

然后让left红指针从左向右找大的数， 让right绿指针从右向左找小的数。只要两个指针都找到了， 那么就让两个指针指向的位置交换数据。 （注意：这里要绿指针先找， 红指针后找，因为keyi指向最左边， 最左边最后放置的应该是比目前keyi所指向的小的数。现在还说不清。 继续向后看）直到两个指针相遇。或者者left红指针在right绿指针右边。然后这个时候最左边keyi指向的数据和两个指针相遇位置的数据交换。 这个时候单趟就结束了。

此时两指针所指向位置就是排好的一个位置， 左边的值一定比两指针指向位置的值小， 右边的值一定比两指针指向位置的值大。

这个过程中keyi和两指针指向的位置交换数据是最后一步， 交换后这一趟结束， 并且交换后两指针指向位置的数据就是原keyi的数据， 并且这个位置的值已经排好。这说明两个值交换之前keyi的值大于两指针指向的数据。造成这个现象的原因就是因为我们先让右指针找， 再让做指针找。 因为右指针找的过程中只有两种情况， 一种是找到了比keyi小的数据，一种是和左指针相遇。而左指针在上一步找到比keyi大的数据后又和一个比keyi小的数据交换了。所以这个时候左指针也是指向的小数据。 所以让右指针先找的话最后两指针相遇的位置一定是一个比keyi小的值。 

而如果让keyi指向最左边的话就要让右指针先动。 原因同上自行分析。

现在来写一下代码：

//霍尔版本
int partSort1(int* a, int left, int right) 
{int get = GetMidIndex(a, left, right);Swap(&a[get], &a[left]);int keyi = left;while (left < right) {//先找右， 防止左右指针相遇的位置是一个比keyi大的数字while (left < right && a[right] >= a[keyi]) //&&左边这里为了相遇后随时能够跳出循环。&&右边加=号是为了防止右指针找到一个和keyi相同的数字， 左指针找到一个和keyi相同的数字，交换后数值不变造成死循环。{right--;}//while (left < right && a[left] <= a[keyi]) {left++;}//Swap(&a[left], &a[right]);//交换左右指针指向的数据}Swap(&a[keyi], &a[left]);//这个left指针指向的一定不会比keyi指向的大。 因为right先找， 找到了也就是找到了， 找不到也会//和left指向同一个位置。 所以不会比keyi大。return left;//返回分割位置.
}

 挖坑法

挖坑法的思想和霍尔的类似， 知识没有霍尔的坑那么多。 

如图：

 

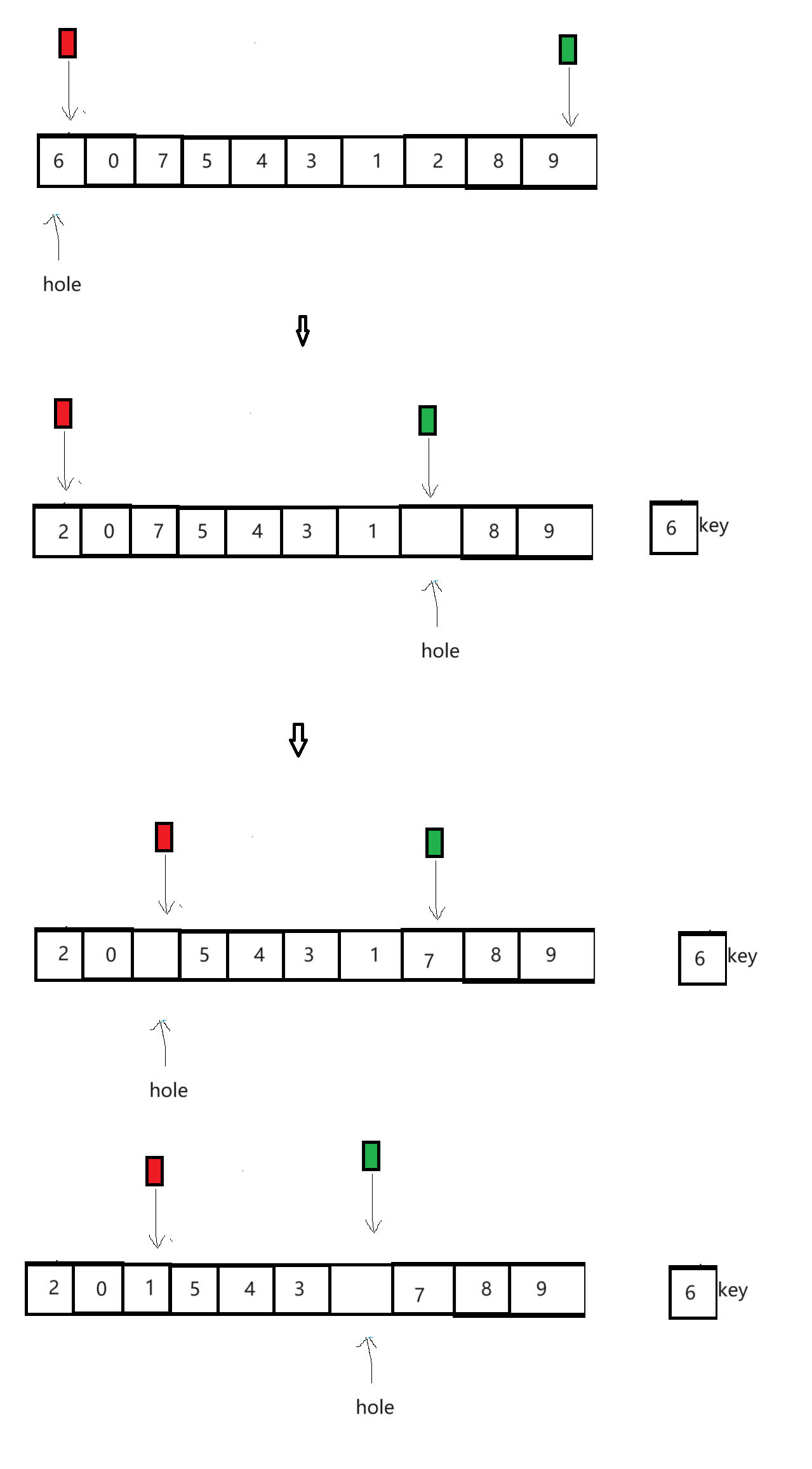
就是让一个变量key保存最左边的值。

然后让一个坑指针指向这个位置， 将这个位置看作没有值。 然后右指针开始找小的（这里就记住， 右边因为比最后的排好位置的值要大， 所以要找小，将这个小的值扔到左边。 左边同样的道理， 因为左边的值要小于那个值， 所以要找大， 然后将大的值扔到右边， 然后霍尔是互相扔， 挖坑是扔到对方挖的坑里面）。找到后将值放到左边的坑里，这里的坑被填了。 然后右指针指向的位置的值相当于没了， 就让坑指向该位置。

往复， 直到两指针相遇， 将保存的key的值放到坑里。这个key的值就是排好的单趟的值。

这里为代码

//挖坑法
int partSort2(int* a, int left, int right) 
{int get = GetMidIndex(a, left, right);Swap(&a[get], &a[left]);int key = a[left];int hole = left;//让hole开始等于坑while (left < right) {while (left < right && a[right] >= key) //右边找小， 所以遇到大于key的就继续向左找{right--;}//找到后就将值给给坑的位置， 然后自己的位置变成坑a[hole] = a[right];hole = right;while (left < right && a[left] <= key) {left++;}a[hole] = a[left];hole = left;}a[hole] = key;return hole;
}

前后指针法

前后指针法不同于上面两种方法， 思想有差别。 

前后指针法的流程就是cur遇不到小的就一路走到底， 遇到小的prev指针就向前追。 同时两个指针的值互相扔给对方。

下图为过程图：

 

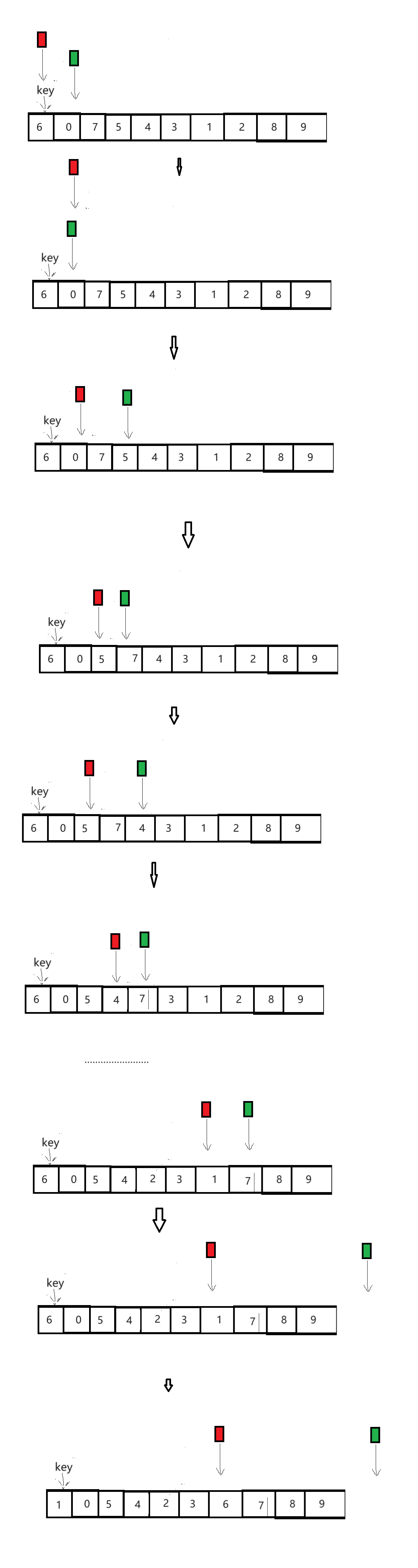
 绿指针cur只要不遇到小于keyi指针指向的值得数就向前走， 遇到得话prev就向前移动一位然后和绿指针cur指向位置交换数据。 直到cur越界退出循环然后prev红指针和keyi指向的位置互换数据。 这个时候prev指向的位置就是排好序的位置。 

以下为代码

//前后指针法
int partSort3(int* a, int left, int right)
{int cur = left + 1;//cur指向第二个数据int prev = left;//prev和keyi都指向第一个数据int keyi = left;int get = GetMidIndex(a, left, right);Swap(&a[get], &a[keyi]);while (cur <= right) //遍历直到cur出了数组范围{if (a[cur] < a[keyi] && ++prev != cur) //cur找小， 只要找到小的， 那么prev++后交换prev和cur的数据。 //找不到小的；cur就一路往前冲。{Swap(&a[prev], &a[cur]);}cur++;}Swap(&a[prev], &a[keyi]);//交换完成之后， prev指向了小于keyi的最后一个数据。 然后keyi的值和prev的值交换。return prev;//返回prev。
}

以上， 三个单趟排序方法都有一个特点， 那就是每趟都排好一个数据， 而且这个数据的前面的数据一定小于这个数据。 后面的数据一定大于这个数据。 

多趟排序

多趟排序分为递归和非递归。

递归

首先来实现递归方法，如下为代码：

//快排递归方法
void QuickSort(int* a, int begin, int end) 
{if (begin >= end) //如果begin >= end说明只剩一个节点， 一个节点就是有序或者区间不存在。 都要返回。{return;}//int keyi = partSort3(a, begin, end);//递归就是分治， 每次单趟排序后都接收一下排好的位置， 然后对这个位置的左边和这个位置的右边再次进行单趟排序。 QuickSort(a, 0, keyi - 1);//分治左树QuickSort(a, keyi + 1, end);//分治右树}

递归就是分治， 每次单趟排序后都接收一下排好的位置， 然后对这个位置的左边和这个位置的右边再次进行单趟排序。 一直分治到只剩下一个节点或者给的排序区间根本不存在。如图：

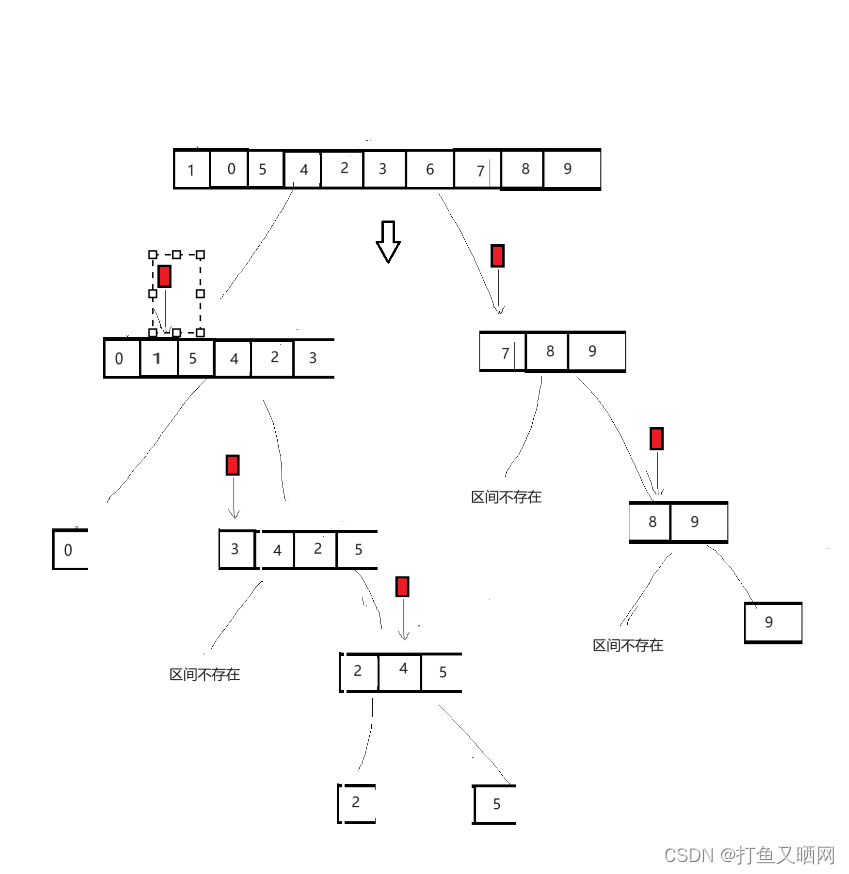
 非递归

这里来使用栈实现非递归。

如下为代码

//快排非递归
void QuickSortRno(int* a, int begin, int end) 
{Stack st;StackInit(&st);//栈初始化//先将第一趟数据压栈StackPush(&st, end);//StackPush(&st, begin);////while (!StackEmpty(&st)) //栈不是空那么就进入循环{//取到左右区间这两个数据。 int left = StackTop(&st);//取出左右区间， 然后进行但趟排序。 StackPop(&st);int right = StackTop(&st);StackPop(&st);//int keyi = partSort3(a, left, right);if (right > keyi + 1) //然后将新的区间压入栈中。 遇到节点或者不存在区间就不能压栈。 然后直到栈中没有数据。 {StackPush(&st, right);StackPush(&st, keyi + 1);}if (keyi - 1 > left) {StackPush(&st, keyi - 1);StackPush(&st, left);}}StackDestroy(&st);}

非递归需要使用栈压入区间。 然后判定排序结束的条件就是栈中无数据。 

这个过程同样是拆解分治的过程。 和递归相同， 递归过程所调用的函数 非递归过程都调用了一遍。 只不过过程不同：递归是函数逐步调用， 层数往深处走。 而非递归是平行的，将需要调用的函数的参数区间保存到栈中， 一个函数调用完成之后继续调用另一个函数。 

其中需要注意的是区间先入的后出。 后入的先出。