目录
- 1. 树的相关概念
- 1.1 简述:树
- 1.2 树的概念补充
- 2. 二叉树
- 2.1 二叉树的概念
- 2.2 二叉树的性质
- 2.3 二叉树的存储结构与堆
- 2.3.1 存储结构
- 2.3.2 堆的概念
- 2.3.3 堆的实现
- 2.3.3.1 堆的向上调整法
- 2.3.3.2 堆的向下调整算法
- 2.3.3.3 堆的实现
1. 树的相关概念
1.1 简述:树
树是一种非线性的数据结构,其有n个有限的节点构成,树结构具有层次性。它的形状颇像一颗颠倒的树,因此而被称为树。
补充:
- 树的结构中有一个特殊的结点,其没有前驱结点,被称为根结点。
- 树的结构中,其子树间不能存在交集,若存在交集,那么,此结构就不能被称为树结构。
1.2 树的概念补充

- 节点的度:一个节点含有的子树的个数称为该节点的度;(A结点的度为3)
- 叶子节点:度为0的结点;(E, F, G, D, H结点)
- 非叶子节点:度不为0的结点(B,C, G结点)
- 父亲节点:若一个节点含有子节点,则这个节点称为其子节点的父节点
- 子节点:一个节点含有的子树的根节点称为该节点的子节点;
- 兄弟节点:具有相同父节点的节点互称为兄弟节点;
- 树的度:一棵树中,最大的节点的度称为树的度;
- 节点的层 :从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
- 树的深度 :树中节点的最大层次;
- 堂兄弟结点 :双亲在同一层的节点互为堂兄弟;
- 祖先结点:从根到该节点所经分支上的所有节点;
- 子孙结点 :以某节点为根的子树中任一节点都称为该节点的子孙;
- 森林: 多棵互不相交的树的集合
2. 二叉树
2.1 二叉树的概念
对于树结构的初次学习,我们来重点学习二叉树这一结构。

由上图可知,二叉树具有两个特点:
- 二叉树是一个结点的集合,可能为空或者由根节点,左子树,右子树构成。
- 二叉树由左右子树之分,所以,二叉树为一个有序树,其顺序不能颠倒。
- 二叉树的没有拥有超过两个孩子结点的结点,即二叉树的度为2。
- 补充:特殊的二叉树
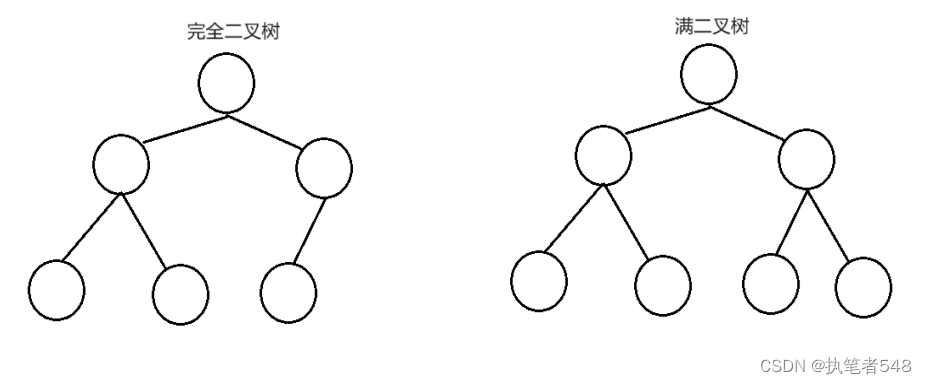
<1> 满二叉树:除叶子结点外,所有结点都有左右孩子结点,若k二叉树的层数,那么满二叉树的结点就有 k 2 k^2 k2 - 1个结点。
<2> 完全二叉树:除最后一层外,所有结点都有左右孩子结点,最后一层叶子结点连续。
2.2 二叉树的性质
- 若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有2^(i - 1) 个结点.
- 若规定根节点的层数为1,则深度为h的二叉树的最大结点数是 2 h 2^h 2h - 1.(等比数列求和)
- 对任何一棵二叉树, 如果度为0其叶结点个数为n, 则其度为0的结点一定比度为2的结点多一个.
- 若规定根节点的层数为1,具有n个结点的满二叉树的深度,h = l o g 2 ( n + 1 ) log_2(n + 1) log2(n+1)
- 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对于序号为i的结点有:
<1> 若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点
<2> 若2i+1<n,左孩子序号:2i+1,2i+1>=n否则无左孩子
<3> 若2i+2<n,右孩子序号:2i+2,2i+2>=n否则无右孩子
2.3 二叉树的存储结构与堆
2.3.1 存储结构
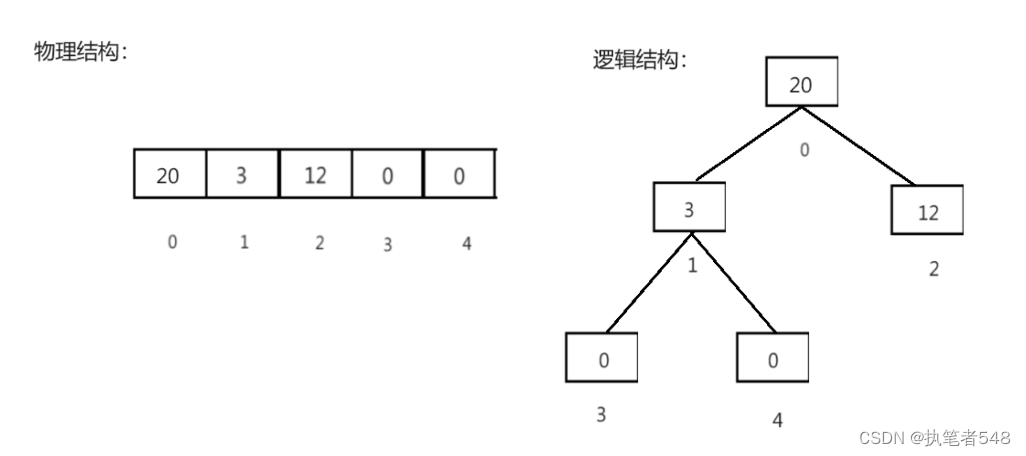
- 顺序存储:
其采用的方式为使用数组进行数据的存储,其各个结点的关系通过下标之间的数学关系来实现,在物理结构上其仍为数组,此结构只适合存储完全二叉树。- 链式存储:
使用链表的方式来存储数据,其存在三个域,数据域,左孩子指针域,右孩子指针域。在逻辑上,呈现链式的逻辑结构。
2.3.2 堆的概念
- 堆是一棵完全二叉树。
- 堆分为大堆与小堆,当所有结点的值都大于孩子结点时即为大堆,当所有结点的值都小于其孩子结点时即为小堆。
2.3.3 堆的实现
- 因为堆都是完全二叉树,这里我们使用顺序存储的方式来进行堆的实现。
- 在数组中若父亲节点的下标为pos,其左孩子的下标为pos × 2 + 1,右孩子结点的下标为pos × 2 + 2,下标为0的元素为根结点。(顺序存储方式,使用数组来实现堆结构的方式)
我们已经知晓了如何判断一个数组是否为堆,可我们对下面两个问题还是没有办法去解决:
- 当一个数组是堆时,我们如何保证在不断向数组中插入数据而堆的结构不被打乱。
- 如何将一个不是堆的数组调整为堆。
- 如何去创建一个是堆的数组。
我们接下来进行这几个问题的学习。
2.3.3.1 堆的向上调整法
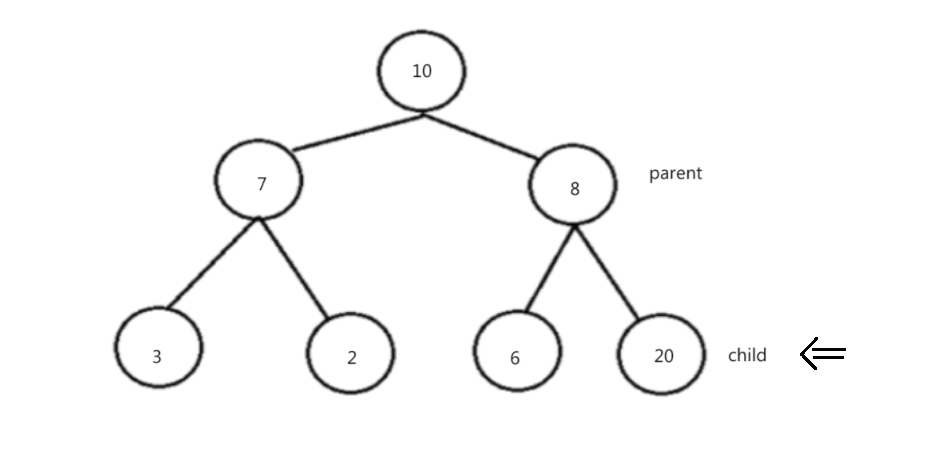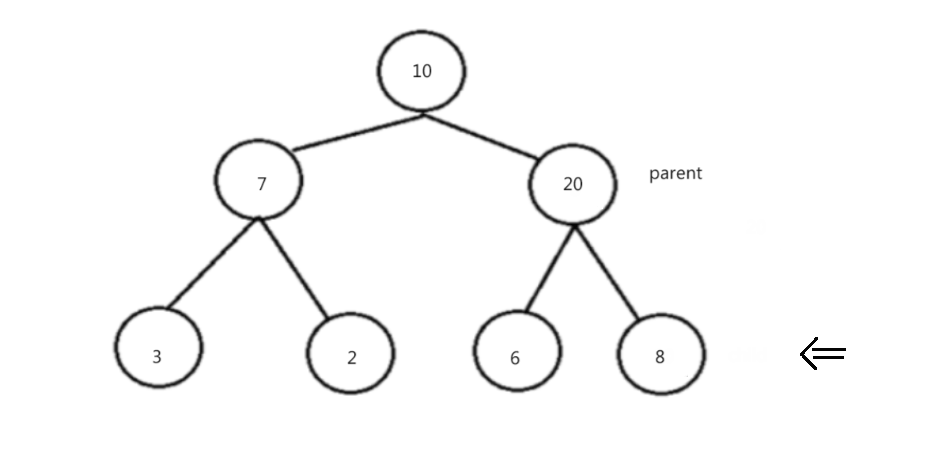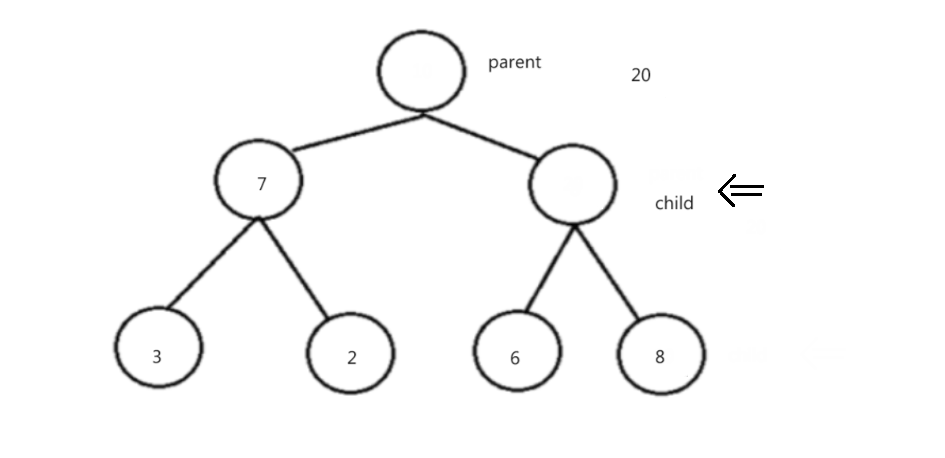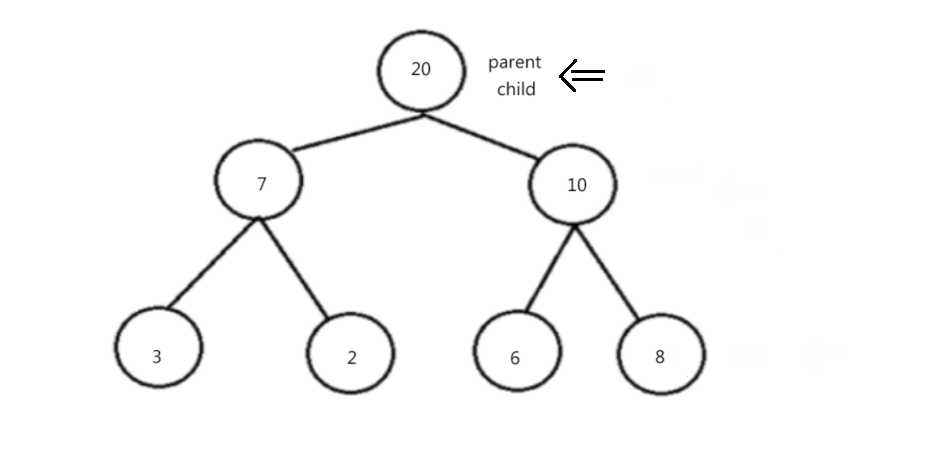
void HeapAdjustUp(int* arr, int child)
{int parent = (child - 1) / 2;while (child > 0){if (arr[parent] < arr[child]){swap(&arr[parent], &arr[child]);child = parent;parent = (child - 1) / 2;}else{break;}}
}
向上调整建堆:
- 将数组中的元素从首元素开始一个一个视作插入已有的堆中在进行向上调整,初始堆为空。
那么,我们就可以进行如下操作:
for(int i = 0; i < n; i++)
{HeapAdjustUp(arr, i);
}
2.3.3.2 堆的向下调整算法
void HeapAdjustDown(int* arr, int n, int parent)
{//n为元素个数int child = parent * 2 + 1;while (child < n){if (child + 1 < n && arr[child] < arr[child + 1]){child++;}if (arr[parent] < arr[child]){swap(&arr[parent], &arr[child]);parent = child;child = parent * 2 + 1;}else{break;}}
}
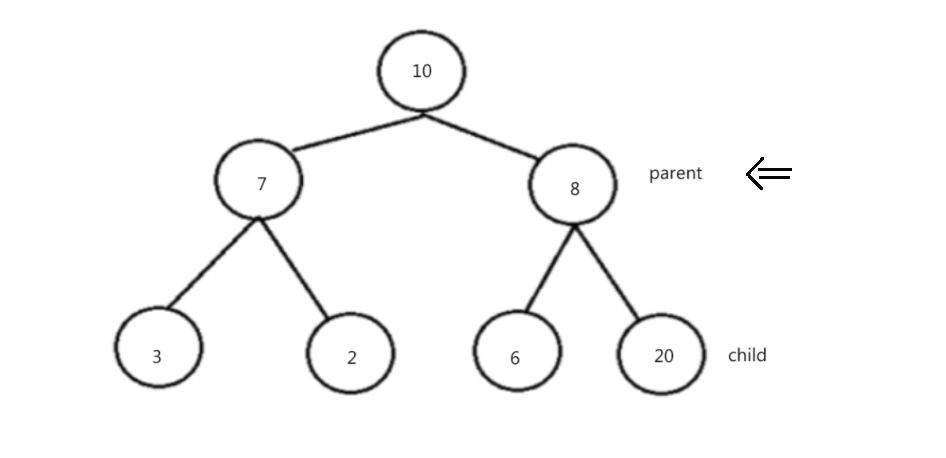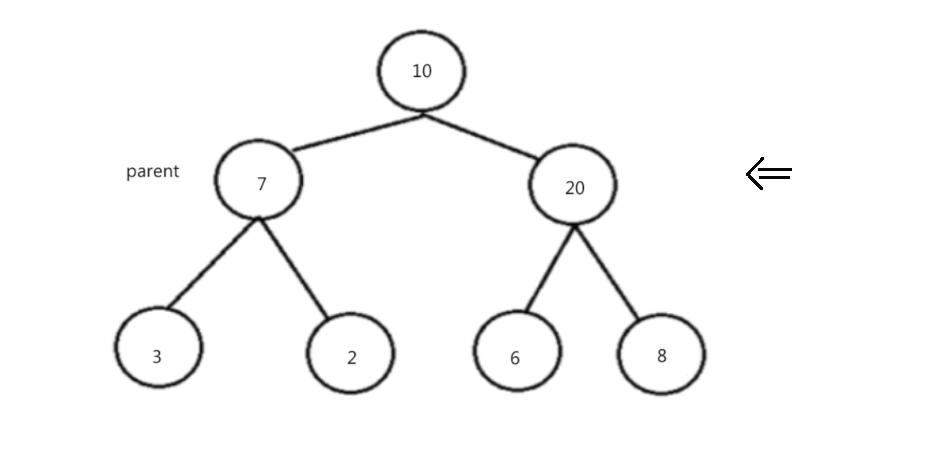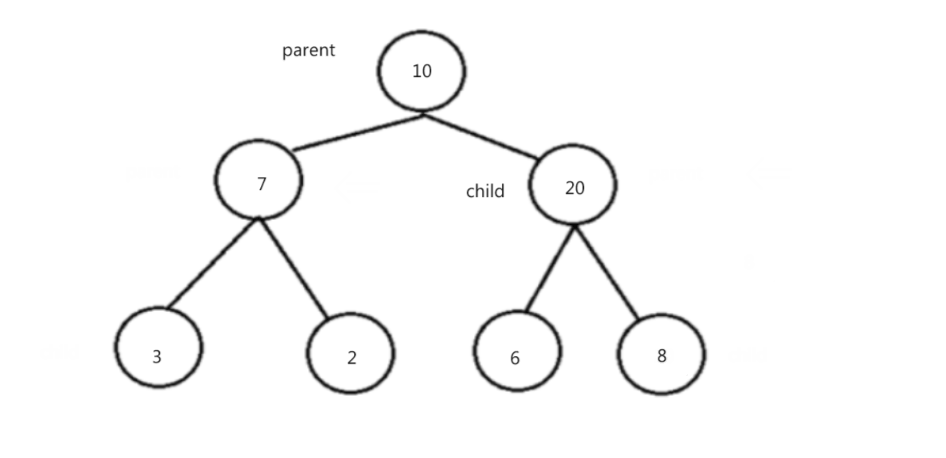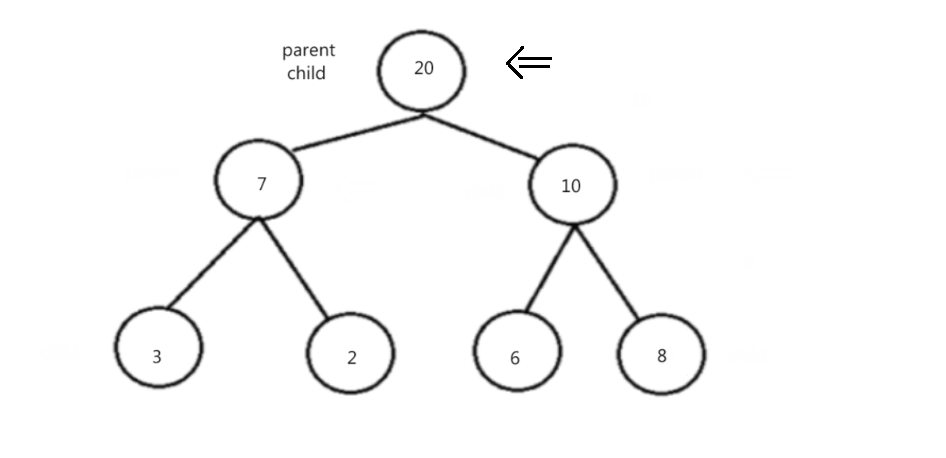
向下调整法建堆:
2. 我们从最后一个非叶子结点开始,向下调整,调整过后的子树都为堆,一直循环到根结点。操作如下:
过程演示:
for (int j = (n - 1 - 1) / 2; j >= 0; j--)
{HeapAdjustDown(arr, n, j);
}
2.3.3.3 堆的实现
堆的结构:
typedef struct Heap
{int* data;int size;int capacity;
}Heap;
堆的初始化与销毁:
void HeapInit(Heap* heap)
{heap->data = NULL;heap->capacity = heap->size = 0;
}void HeapDestroy(Heap* heap)
{while (heap->size){HeapPop(heap);}free(heap->data);heap->data = NULL;heap->capacity = heap->size = 0;
}
堆的元素增加与头删:
void CheckCapacity(Heap* heap)
{if (heap->size == heap->capacity){int newcapacity = heap->capacity == 0 ? 4 : heap->capacity * 2;int* tmp = (int*)realloc(heap->data, newcapacity * sizeof(int));if (tmp == NULL){perror("malloc failed");exit(-1);}heap->data = tmp;heap->capacity = newcapacity;}
}void HeapPush(Heap* heap, int val)
{CheckCapacity(heap);heap->data[heap->size] = val;heap->size++;HeapAdjustUp(heap->data, heap->size - 1);
}//逆置首尾元素,size--,再向下调整
//向下调整后堆仍为堆的前置条件为,左右子树都为堆
void HeapPop(Heap* heap)
{assert(!HeapEmpty(heap));swap(&heap->data[0], &heap->data[heap->size - 1]);heap->size--;//左右子树都为堆HeapAdjustDown(heap->data, heap->size, 0);
}返回堆顶元素与判空:
bool HeapEmpty(Heap* heap)
{return heap->size == 0;
}int HeapTop(Heap* heap)
{assert(!HeapEmpty(heap));return heap->data[0];
}