先来一个题衔接一下：

与上一题的思路差不多，不过这里有几点需要注意：

1.因为某一列的状态还与上上一行有关，因此我们令f[i][j][k]表示第i行状态为j,第i-1行状态为k的最大炮兵数。

因此，我们可以得到状态转移方程：f[i][j][k]=max(f[i][j][k],f[i-1][k][q]+num[j])其中我们保证j,k,q不冲突并且自己可以。

2.注意到直接开存不下，我们考虑用vector存符合条件的，并计算一下有几个再开空间。

下面是AC代码：

#include<bits/stdc++.h>
using namespace std;
int n,m,a[110],dp[110][70][70];
vector<int> st;
char b;
vector<int> num;
int calc(int num){int ans=0;while(num){if((num&1)==1) ans++;num>>=1;}return ans;
}
int main(){cin>>n>>m;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){scanf(" %c",&b);if(b=='H'){a[i]|=(1<<(j-1));}}}for(int i=0;i<=(1<<m)-1;i++){if(i&(i<<1)) continue;if(i&(i<<2)) continue;st.push_back(i);num.push_back(calc(i));}int ans=0;for(int i=1;i<=n;i++){for(int j=0;j<st.size();j++){if((a[i]&st[j])) continue;for(int k=0;k<st.size();k++){if((a[i-1]&st[k])) continue;if((st[k]&st[j])) continue;for(int q=0;q<st.size();q++){if(i>=2){if((a[i-2]&st[q])) continue;}if((st[k]&st[q])) continue;if((st[q]&st[j])) continue;dp[i][j][k]=max(dp[i][j][k],dp[i-1][k][q]+num[j]);ans=max(ans,dp[i][j][k]);}}}}cout<<ans;
}

首先，什么是TSP问题？

即给你一张抽象的图，求从某一个起点出发，经过所有点的最短路径。

如何解决呢？

我们先建立一个超级源点，这就解决了从某一个起点出发的问题，然后，我们假设走了134，现在在5，那么后来的267是与134的走法无关的，因此我们只要保留最短的即可，即DP。

因此，我们可以令f[st][i]表示当前状态为st,最后到达的一个点为i所经过的最短路径。

访问过标1，未访问标0.

转移方程为f[st][i]=min(f[st'][j]+a[j][i]).（st'=st-1<<(i-1)).

若为必须回到原点，那么走出来的一定是一个圈，因此我们固定1为起点，然后在原来的结果上加上终点与1的边。

下面是实现代码：

#include<bits/stdc++.h>
using namespace std;
int n,m,a[25][25],dp[1<<20][25];
int f(int st,int x){if(dp[st][x]<=1e9){return dp[st][x];}int stt=st-(1<<(x-1));for(int i=1;i<=n;i++){if(a[i][x]==0) continue;if((stt>>(i-1))&1){dp[st][x]=min(dp[st][x],a[i][x]+f(stt,i));}}return dp[st][x];
}
int main(){cin>>n>>m;for(int i=1;i<=m;i++){int x,y,z;cin>>x>>y>>z;a[x][y]=z;a[y][x]=z;}memset(dp,0x7f,sizeof(dp));dp[1][1]=0;int ans=0x7f7f7f7f;int st=(1<<n)-1;for(int i=2;i<=n;i++){int tmp=f(st,i);if(a[i][1]!=0) ans=min(ans,a[i][1]+tmp);}cout<<ans;
} 

我们来看一个类似的问题：

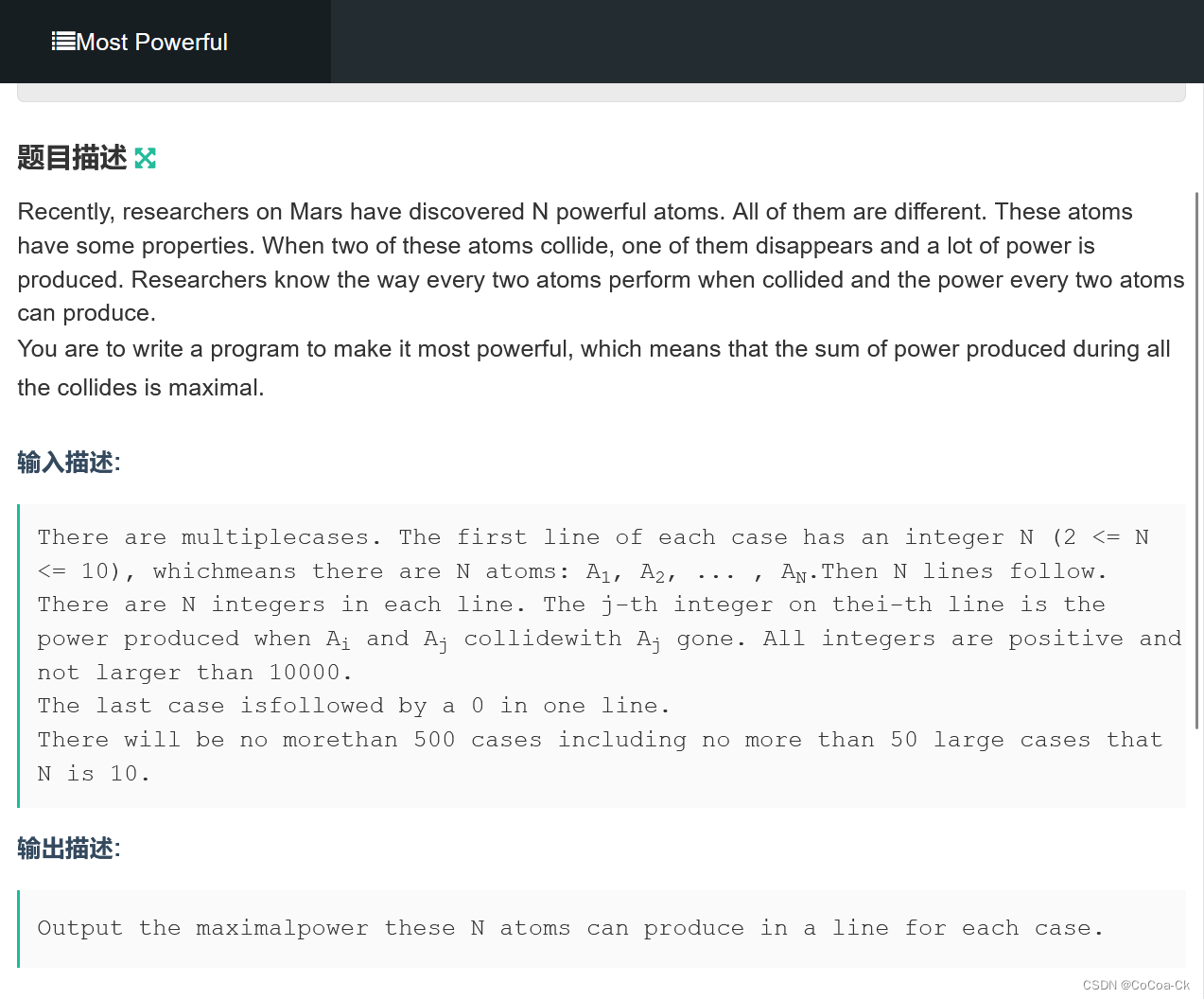
思路类似，我们令f[i]表示状态为i时获得的最大能量。

其中第k位==1表示它已经用了并消失，为0表示没有用或用了没消失。

易得状态转移方程：f[k|(1<<(i-1)]=max(f[k]+a[j][i]).我们转换一下：

f[k]=max(f[k']+a[j][i])(其中k'的i与j位为0，k=k'+1<<(i-1))

下面是AC代码：

#include<bits/stdc++.h>
using namespace std;
int n,a[14][14],x,f[2000];
int main(){while(cin>>n){memset(f,0,sizeof(f));if(n==0) break;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){scanf("%d",&x);a[i][j]=x;}}int ans=0;for(int i=1;i<=(1<<n)-2;i++){for(int k=0;k<i;k++){for(int ii=1;ii<=n;ii++){if((k>>(ii-1))&1) continue;for(int jj=1;jj<=n;jj++){if((k>>(jj-1))&1) continue;if(i!=(k|(1<<(jj-1)))) continue;f[i]=max(f[i],f[k]+a[ii][jj]);ans=max(ans,f[i]);}}}}printf("%d\n",ans);}
}