C++ 前缀和-编程知识

例1

例2

例3

例4

例5

例6

例7

例8

例1

DP34 【模板】前缀和

分析：dp和arr的大小并不是固定的，就是有没有偏移量，这里的n是从1开始，不如直接放到下标1处，在最后的减法时，如果用第一个参考代码会下标越界到-1，所以说这里的方法并不是固定的，思路，偏移量理清了静下心就可以上手写

注意：a[i] 的最大值是INT_MAX，所以创建long long 类型的dp表

参考代码:dp[n + 1],arr[n + 1]

#include <iostream>
using namespace std;
#include <vector>
int main() {int n = 0, q = 0;cin >> n >> q;vector<int> arr(n + 1);for(int i = 1; i < n + 1; i++)cin >> arr[i];vector<long long> dp(n + 1);for(int i = 1; i < n + 1; i++)dp[i] = dp[i - 1] + arr[i];int l = 0, r = 0;while(q--){cin >> l >> r;cout << dp[r] - dp[l - 1] << endl;}return 0;
}
// 64 位输出请用 printf("%lld")

参考代码: dp[n],arr[n]

#include <iostream>
using namespace std;
#include <vector>
int main() {int n = 0, q = 0;cin >> n >> q;vector<int> arr(n);for(int i = 0; i < n; i++)cin >> arr[i];vector<long long> dp(n);dp[0] = arr[0];for(int i = 1; i < n; i++)dp[i] = dp[i - 1] + arr[i];int l = 0, r = 0;while(q--){cin >> l >> r;cout << dp[r - 1] - dp[l - 1] + arr[l - 1] << endl;}return 0;
}
// 64 位输出请用 printf("%lld")

参考代码：dp[n],arr[n + 1]

#include <iostream>
using namespace std;
#include <vector>
int main() {int n = 0, q = 0;cin >> n >> q;vector<int> arr(n + 1);for(int i = 1; i <= n; i++)cin >> arr[i];vector<long long> dp(n);dp[0] = arr[1];for(int i = 1; i < n; i++)dp[i] = dp[i - 1] + arr[i + 1];int l = 0, r = 0;while(q--){cin >> l >> r;cout << dp[r - 1] - dp[l - 1] + arr[l] << endl;}return 0;
}
// 64 位输出请用 printf("%lld")

例2

DP35 【模板】二维前缀和

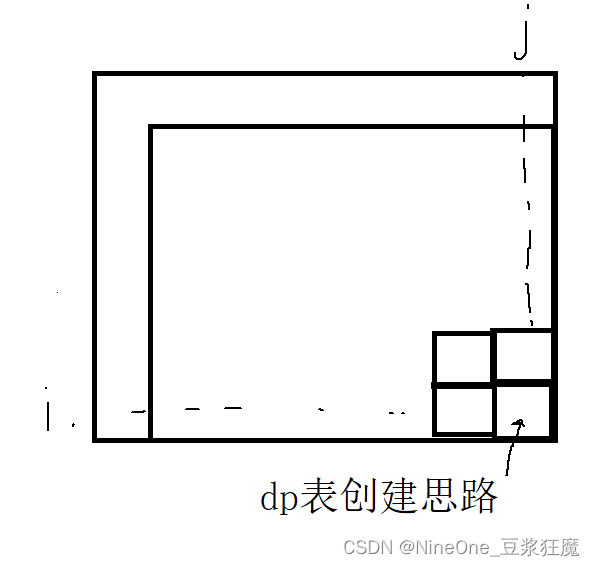
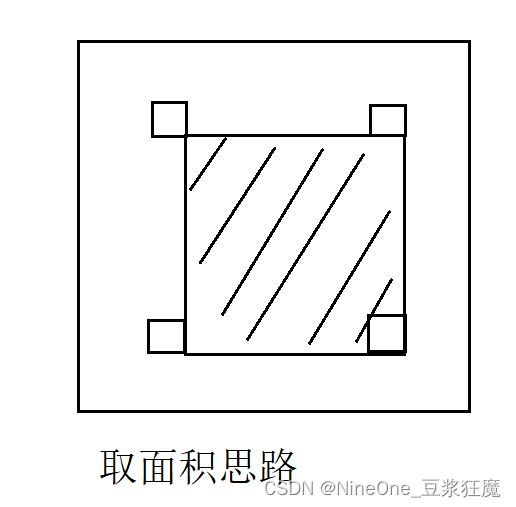
dp和原数组对齐了，就没有偏移量

注意：a[i][j] 的最大值是INT_MAX，所以创建long long 类型的dp表

参考代码

#include <iostream>
using namespace std;
#include <vector>
int main() {int n = 0, m = 0, q = 0;cin >> n >> m >> q;vector<vector<int>> arr(n + 1, vector<int>(m + 1));for(int i = 1; i < n + 1; i++)for(int j = 1; j < m + 1; j++)cin >> arr[i][j];vector<vector<long long>> dp(n + 1, vector<long long>(m + 1));for(int i = 1; i < n + 1; i++)for(int j = 1; j < m + 1; j++)dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + arr[i][j];while(q--){int x1 = 0, y1 = 0, x2 = 0, y2 = 0;cin >> x1 >> y1 >> x2 >> y2;cout << dp[x2][y2] - dp[x2][y1 - 1] - dp[x1 - 1][y2] + dp[x1 - 1][y1 - 1] << endl; }return 0;
}

例3

724. 寻找数组的中心下标

要点：f[i] = f[i - 1] + nums[i - 1];就是看后面的nums，如果是i - 1，就是不包括自己的前缀和，f[0]自然是0，这题包不包括都可以，包括就是等式两边同时加上自己这个元素，

参考代码

class Solution {
public:int pivotIndex(vector<int>& nums) {int n = nums.size();vector<int> f(n), g(n);for(int i = 1; i < n ; i++)f[i] = f[i - 1] + nums[i - 1];for(int i = n - 2; i >= 0; i--)g[i] = g[i + 1] + nums[i + 1];for(int i = 0; i < n; i++)if(f[i] == g[i])return i;return -1;}
};

例4

238. 除自身以外数组的乘积

注意点：f[0] = 1， g[n - 2] = 1

参考代码

class Solution {
public:vector<int> productExceptSelf(vector<int>& nums) {int n = nums.size();vector<int> f(n), g(n), ret(n);f[0] = g[n - 1] = 1;for(int i = 1; i < n; i++)f[i] = f[i - 1] * nums[i - 1];for(int i = n - 2; i >= 0; i--)g[i] = g[i + 1] * nums[i + 1];for(int i = 0; i < n; i++)ret[i] = f[i] * g[i];return ret;}
};

例5

560. 和为 K 的子数组

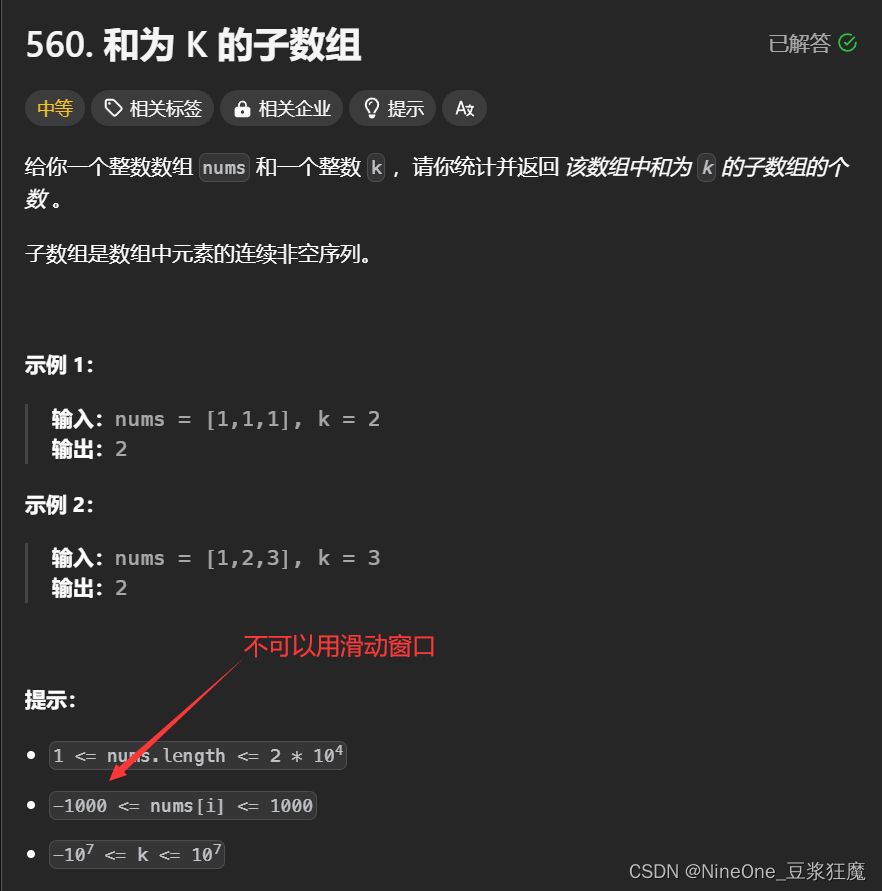
可以不用前缀和，因为这里不需要用到下标随机访问，这里只需要顺序访问

这里不可以用滑动窗口：因为没有单调性

把有的sum都放到哈希表里就行，先判断 : hash.count(sum) 再放入哈希表

注意：这里有个hash[0] = 1，sum = k时候也是符合条件，但是哈希表里没有hash[0]，(但是之后是会可能会添加上hash[0]，就是中间有个地方前缀和为0)，总的来说就是少了一个起点0

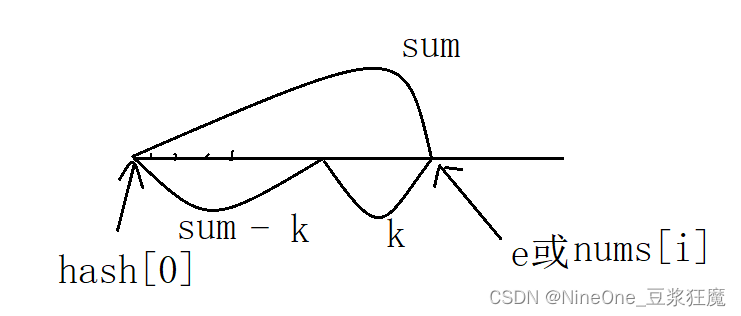
参考代码

class Solution {
public:int subarraySum(vector<int>& nums, int k) {// int n = nums.size(), ret = 0;// vector<int> dp(n);// dp[0] = nums[0];// for(int i = 1; i < n; i++)//     dp[i] = dp[i - 1] + nums[i];// unordered_map<int, int> hash;// hash[0] = 1;// for(auto e : dp)// {//     if(hash.count(e - k)) ret += hash[e - k];//hash[e - k]//     hash[e]++;// }// // for(int i = 0; i < n; i++)// // {// //     if(hash.count(dp[i] - k)) ret += hash(dp[i] - k);// //     hash[dp[i]]++;// // }// return ret;unordered_map<int, int> hash;hash[0] = 1;int sum = 0, ret = 0;for(int i = 0; i < nums.size(); i++){sum += nums[i];if(hash.count(sum - k)) ret += hash[sum - k];hash[sum]++;}return ret;}
};

例6

974. 和可被 K 整除的子数组

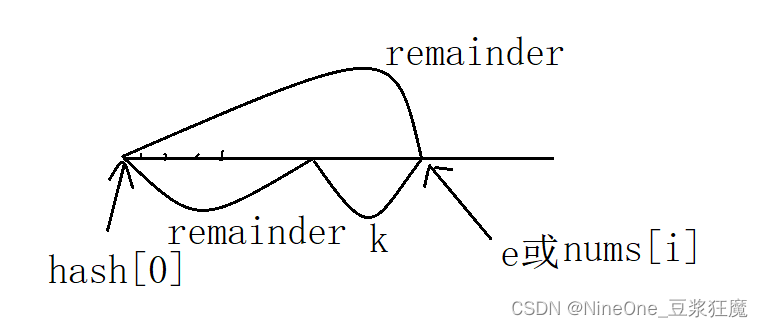
参考代码

class Solution {
public:int subarraysDivByK(vector<int>& nums, int k) {unordered_map<int, int> hash;hash[0] = 1;int sum = 0, ret = 0;for(int i = 0; i < nums.size(); i++){sum += nums[i];if(hash.count((sum % k + k) % k)) ret += hash[(sum % k + k) % k];hash[(sum % k + k) % k]++;}return ret;}
};

例7

525. 连续数组

题解：把0 改成 -1，之后求和为0的最长子数组，有负数，自然不能用滑动窗口

因为求的是长度吗，那么这里就是最短索引和前缀和的映射，<前缀和，最小索引>

因为是顺序遍历，那么不存在就添加进哈希表，这样就可以得到最小索引，既可以不用dp表，也直接找到最小索引

注意：这样就可以理解为什么是i - hash[sum]

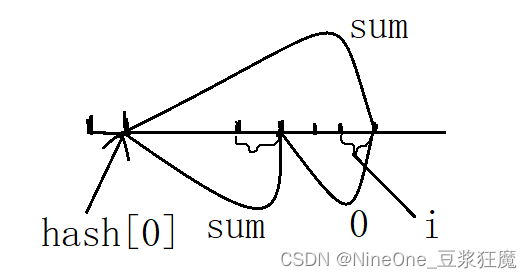
参考代码

class Solution 
{
public:int findMaxLength(vector<int>& nums) {unordered_map<int, int> hash;int sum = 0, ret = 0;hash[0] = -1;// for(auto e : nums)// {//     sum += e == 0 ? -1 : e;//     if(hash.count(sum)) ret = max(ret, );//     else hash[sum]++;// }for(int i = 0; i < nums.size(); i++){sum += nums[i] == 0 ? -1 : 1;if(hash.count(sum)) ret = max(ret, i - hash[sum]);else hash[sum] = i;}return ret;}
};

例8

1314. 矩阵区域和

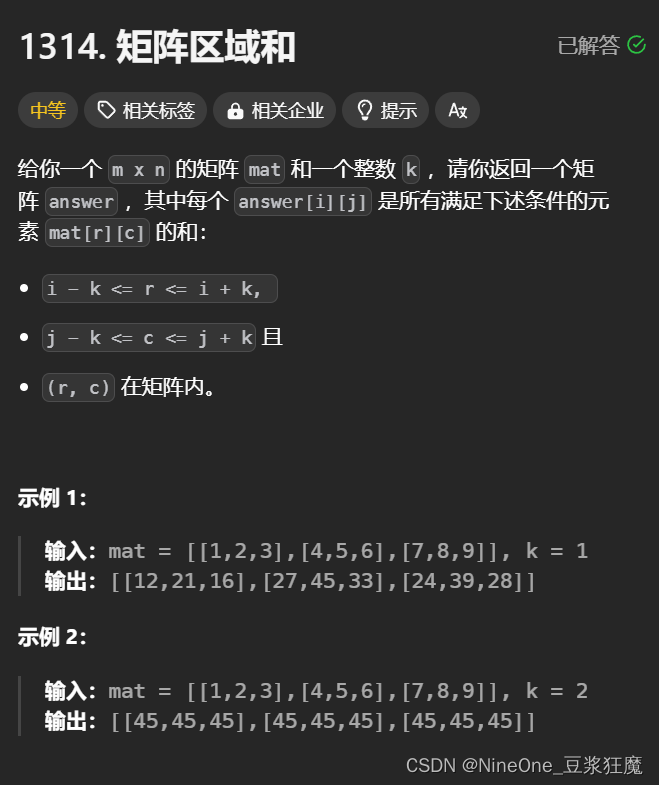
分析：涉及偏移量，和对越界的处理，如果二维dp不是行列 + 1那么边界情况就麻烦了，一维dp若不是n + 1 只有开头或者结尾处理，

偏移：mat 到dp 的偏移，dp 到 ret的偏移

注意：int x2 = min(i + k, m - 1) + 1, y2 = min(j + k, n - 1) + 1;我在写的时候错在不是m - 1

参考代码

class Solution {
public:vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {int m = mat.size(), n = mat[0].size();vector<vector<int>> dp(m + 1, vector<int>(n + 1));for(int i = 1; i < m + 1; i++)for(int j = 1; j < n + 1; j++)dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + mat[i - 1][j - 1];vector<vector<int>> ret(m, vector<int>(n));for(int i = 0; i < m; i++)for(int j = 0; j < n; j++){int x1 = max(i - k, 0) + 1, y1 = max(j - k, 0) + 1;int x2 = min(i + k, m - 1) + 1, y2 = min(j + k, n - 1) + 1;ret[i][j] = dp[x2][y2] - dp[x2][y1 - 1] - dp[x1 - 1][y2] + dp[x1 - 1][y1 - 1];}return ret;}
};