前缀和算法题（区间次方和、小蓝平衡和、大石头的搬运工、最大数组和）-编程知识

一、前缀和的原理和特点

prefix表示前缀和，前缀和由一个用户输入的数组生成。对于一个数组a[]（下标从1开始），我们定义一个前缀和数组prefix[]，满足：

prefix有一个重要的特性，可以用于快速生成prefix:

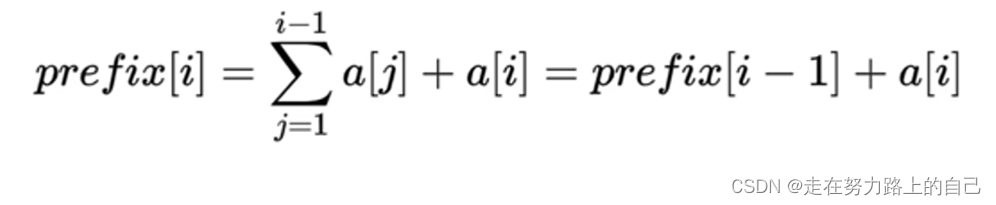
prefix可以O(1)的求数组a[]的一段区间的和:

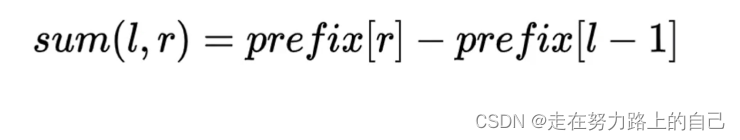
但是注意，prefix是一种预处理算法，只适用于a数组为静态数组的情况，即a数组中的元素在区间和查询过程中不会进行修改。

如果需要实现“先区间修改，再区间查询”可以使用差分数组，如果需要“一边修改，一边查询”需要使用树状数组或线段树等数据结构。

二、实现前缀和

利用前面讲过的特性:prefix[i]= prefix[i - 1] + a[i]我们的数组下标均从1开始，a[0]=0，从前往后循环计算即可。

for(int i = 1;i <= n; ++ i)
prefix[i]= prefix[i - 1] + a[i];

求区间和:
sum(L, R) = prefix[R]-prefix[L - 1]

三、例题

（一、区间次方和）

用户登录

问题描述
给定一个长度为 n 的整数数组 a 以及 m 个查询。
每个查询包含三个整数 l,r,k 表示询问 l~r ,之间所有元素的 k 次方和。
请对每个查询输出一个答案，答案对 1e9+7取模。
输入格式
第一行输入两个整数 n,m 其含义如上所述。
第二行输入 n 个整数 a[1], a[2],…, a[n]。
接下来 m 行，每行输入三个整数 l,r,k 表示一个查询。
输出格式
输出 m 行，每行一个整数，表示查询的答案对 1e9+7 取模的结果。

由于k比较小，所以我们可以处理出五个数组分别表示不同的次方，例如a[3][]中的元素都是数组a中元素的3次方。再对五个数组预处理出前缀和，对于每次询问利用前缀和的性质可O(1)解决。

#define  _CRT_SECURE_NO_WARNINGS 1
#include<bits/stdc++.h>using namespace std;using ll = long long;
const ll p = 1e9 + 7;
const int N = 1e5 + 9;
ll a[6][N], prefix[6][N];
// 设置a[6]的原因:
// 由于 k 较小(1 ~ 5), 可以直接计算各个数的 1 ~ k次方int main()
{ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);int n, m; cin >> n >> m;// 输入两个整数 n,m // n 表示 a[] 数组中有 n 个元素for (int i = 1; i <= n; ++i)cin >> a[1][i]; // 输入 n 个整数for (int i = 2; i <= 5; ++i)for (int j = 1; j <= n; ++j)a[i][j] = a[i - 1][j] * a[1][j] % p;// 求 a[]各个数的 1 ~ 5的次方和for (int i = 1; i <= 5; ++i)for (int j = 1; j <= n; ++j)prefix[i][j] = (prefix[i][j - 1] + a[i][j]) % p;// 求 a[j] 的前缀和取余while (m--){int l, r, k; cin >> l >> r >> k;cout << (prefix[k][r] - prefix[k][l - 1] + p) % p << '\n';// 求数组a[]的(l, r)的和:}return 0;
}

（二、小蓝平衡和）

问题描述
平衡串指的是一个字符串，其中包含两种不同字符，并且这两种字符的数量相等。
例如，ababab和 aababb 都是平衡串，因为每种字符各有三个，而 ababab和 aaaab 都不是平衡串，因为它们的字符数量不相等。
平衡串在密码学和计算机科学中具有重要应用，比如可以用于构造哈希函数或者解决一些数学问题。
小郑拿到一个只包含 L、Q 的字符串，他的任务就是找到最长平衡串，且满足平衡串的要求，即保证子串中 L、Q 的数量相等。
输入格式
输入一行字符串，保证字符串中只包含字符 L、Q.
输出格式
输出一个整数，为输入字符串中最长平衡串的长度。

将L看做1，Q看做-1，只有当某个区间的和为0时，字符串是平衡的。
我们可以预处理出前缀和，然后枚举所有区间(这一步的时间复杂度是O(n^2)的)，得到所有平衡区间的长度最后取大输出即可。

#define  _CRT_SECURE_NO_WARNINGS 1
#include<bits/stdc++.h>using namespace std;
const int N = 1010;char s[N];int prefix[N];int main()
{cin >> s + 1;// 从数组s的第2个位置开始读取字符串（即跳过s[0]），这样字符串的下标就从1开始了  int n = strlen(s + 1);// 计算字符串的长度(从 s[1] 开始计算)for (int i = 1; i <= n; ++i)prefix[i] = prefix[i - 1] + (s[i] == 'L' ? 1 : -1);// 求各个 (1, i) 的前缀和, 如果是 'L' 则加一int ans = 0;for (int i = 1; i <= n; ++i)for (int j = 1; j <= n; ++j)// 遍历所有可能出现平衡串的串if (prefix[j] - prefix[i - 1] == 0)ans = max(ans, j - i + 1);// 得到最大值		cout << ans << '\n';return 0;
}

（三、大石头的搬运工）

用户登录

问题描述
在一款名为”大石头的搬运工“的游戏中，玩家需要操作一排 n 堆石头，进行n -1轮游戏。
每一轮，玩家可以选择一堆石头，并将其移动到任意位置。
在n-1轮移动结束时，要求将所有的石头移动到一起(即所有石头的位置相同)即为成功。
移动的费用为石头的重量乘以移动的距离。例如，如果一堆重量为2 的石头从位置 3 移动到位置 5，那么费用为 2 x(5 -3)= 4。
请计算出所有合法方案中，将所有石头移动到一起的最小费用。
可能有多堆石头在同一个位置上，但是一轮只能选择移动其中一堆。
输入格式
第一行一个整数 n，表示石头的数量。
接下来几行，每行两个整数 w;和pi，分别表示第之个石头的重量和初始位置。
输出格式
输出一个整数，表示最小的总移动费用。

解法一：

#include <bits/stdc++.h>
// 包含所有标准库// 绝对值表达式 |x-1| + |x-2| + |x-6| + |x-13| 取最小值时，x取中位数时最小。
// 在一组石头"坐标-重量"对应的情况下，找到一个位置x，使得移动所有石头到这个位置的总成本最小（成本定义为每个石头的重量乘以其到x的距离）。using Pair = std::pair<int, int>;
// Pair类型用来存储石头的重量和初始位置using LL = long long; // 长整型，用来处理可能的大数字void solve(const int& Case) {int n; std::cin >> n; // n是石头的数量std::vector<Pair> a(n); // Pair的向量，存储石头的重量和初始位置LL sw = 0; // sw是所有石头的总重量for (auto& [w, p] : a) std::cin >> w >> p, sw += w; // 输入每个石头的重量和位置，并更新总重量swstd::sort(a.begin(), a.end()); // 按石头的位置进行排序LL nw = 0; // nw是当前处理过的石头的总重量int x = 0; // x是使得总成本最小的位置// 遍历排序后的石头，寻找满足nw * 2 < sw <= nw + w * 2的xfor (const auto& [w, p] : a) {if (nw * 2 < sw && sw <= (nw + w) * 2) {x = p; // 当前位置p是满足条件的xbreak;}nw += w; // 更新当前处理过的石头的总重量nw}LL ans = 0; // 总成本for (const auto& [w, p] : a) {ans += (LL)w * std::abs(p - x); // 计算每个石头移动到x的成本并累加到ans}std::cout << ans << '\n'; // 输出总成本
}int main() {std::ios::sync_with_stdio(false); // 同步标准C++和C的流，通常可以加速输入输出std::cin.tie(nullptr); // 解绑cin和cout的绑定，通常可以加速输入输出std::cout.tie(nullptr);int T = 1; // 测试用例的数量，默认为1for (int i = 1; i <= T; ++i) solve(i); // 处理每一个测试用例return 0;
}

解法二：

解题思路

首先，我们需要明白在这个问题中，每一次移动的石头的位置并不影响后续的移动，也就是说，无论我们怎么移动石头，最后的总费用只依赖于每个石头最后的位置，而与移动的顺序无关。这个性质使得我们可以逐一考虑每个石头最后的位置，并比较得出最小的总费用。

然后，我们需要分析一下如何计算每一种放置石头的方式的总费用。一种直观的方法是，对于每个石头，我们都计算它被移动到目标位置的费用，然后将这些费用加总。但这样的计算方式在本题的数据范围下是无法接受的。我们需要寻找一种更优的方法。

这里，我们可以运用前缀和的思想。考虑到石头移动的费用与其重量和距离有关，我们可以先将石头按位置排序，然后计算每个石头移动到任一位置的费用，再利用前缀和的方法将这些费用累加起来。具体地，我们可以定义两个数组 pre 和 nex，其中 pre[i] 表示前 i 个石头都移动到第 i 个石头的位置的总费用，nex[i] 表示第 i 个石头之后的所有石头都移动到第 i 个石头的位置的总费用。这样，对于每个石头，我们就可以在 O(1) 的时间内算出所有石头都移动到它的位置的总费用。

时间复杂度分析

整个过程中，排序的时间复杂度是 O(nlogn)，计算 pre 和 nex 的时间复杂度是 O(n)，查找 pre+nex 的最小值的时间复杂度是 O(n)，所以总的时间复杂度是 O(nlogn)。

#include <iostream>
#include <cstring>
#include <algorithm>#define x first // 简化pair中位置的访问
#define y second // 简化pair中重量的访问using namespace std;typedef long long LL;
typedef pair<int, int> PII; 
// pair类型用来存储石头的重量和初始位置 const int N = 1e5 + 10;int n; // n, 表示石头的数量
PII q[N]; // 存储每个石头的位置和重量的数组
LL pre[N], nex[N];// 前缀和数组,后缀和数组int main()
{cin >> n; // n, 表示石头的数量for (int i = 1; i <= n; ++i)cin >> q[i].y >> q[i].x;// 输入 重量 w 和 初始位置 psort(q + 1, q + n + 1);// 按石头的位置进行排序LL s = 0; // 统计总重量for (int i = 1; i <= n; ++i){pre[i] = pre[i - 1]; // 计算当前石头前的总成本pre[i] += s * (q[i].x - q[i - 1].x);// 累加前缀和s += q[i].y;// 更新总重量}s = 0; // 重置总重量, 用于计算后缀和for (int i = n; i >= 1; --i){nex[i] = nex[i + 1]; // 计算当前石头后的总成本nex[i] += s * (q[i + 1].x - q[i].x);// 累加后缀和s += q[i].y;// 更新总重量}LL res = 1e18;for (int i = 1; i <= n; ++i)res = min(res, pre[i] + nex[i]);// 找到移动所有石头的最小总成本cout << res << endl;return 0;
}

（四、最大数组和）

用户登录

问题描述
小明是一名勇敢的冒险家，他在一次探险途中发现了一组神秘的宝石，这些宝石的价值都不同。但是，他发现这些宝石会随着时间的推移逐渐失去价值，因此他必须在规定的次数内对它们进行处理。
小明想要最大化这些宝石的总价值。他有两种处理方式
1.选出两个最小的宝石，并将它们从宝石组中删除。
2.选出最大的宝石，并将其从宝石组中删除。
现在，给你小明手上的宝石组，请你告诉他在规定的次数内，最大化宝石的总价值是多少。
输入格式
第一行包含一个整数 t，表示数据组数。
对于每组数据，第一行包含两个整数几和ん，表示宝石的数量和规定的处理次数。
第二行包含 n 个整数 a1,a2,…., an，表示每个宝石的价值。
输出格式
对于每组数据，输出一个整数，表示在规定的次数内，最大化宝石的总价值。

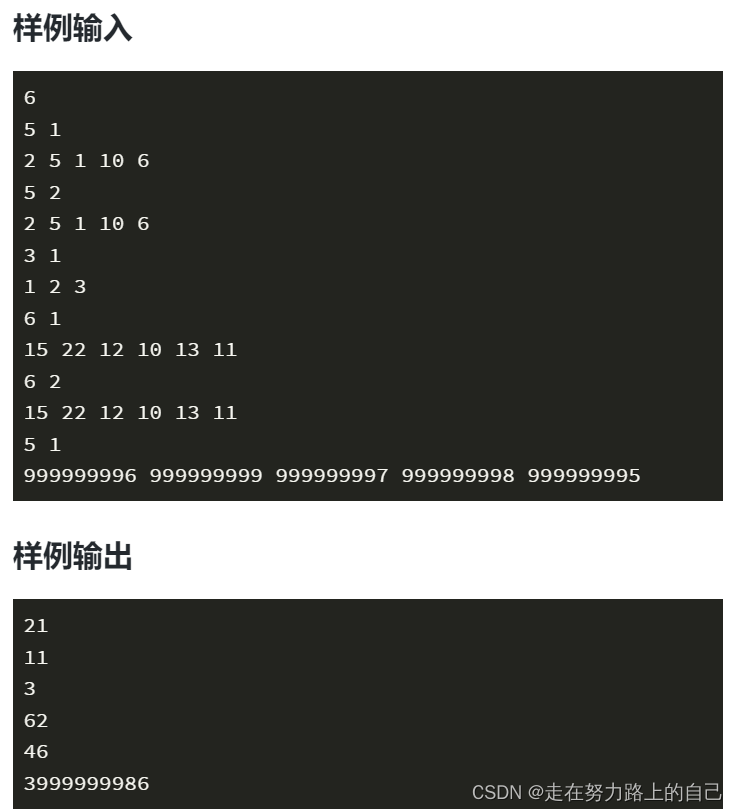
样例输入：

6 5 1 2 5 1 10 6 5 2 2 5 1 10 6 3 1 1 2 3 6 1 15 22 12 10 13 11 6 2 15 22 12 10 13 11 5 1 999999996 999999999 999999997 999999998 999999995

样例输出：

21 11 3 62 46 3999999986

解法一：

解题思路

首先，我们想到了一种贪心的解法，每次删除价值和更小的两个宝石或者删除价值最大的宝石，根据哪种操作可以删除价值更小的宝石。然而，这种方法甚至在示例上都不适用，我们需要更优的解法。

注意到操作的顺序并不重要：删除两个最小的宝石然后再删除最大的宝石与先删除最大的宝石然后再删除两个最小的宝石的操作是相同的。因此，我们可以假设删除了最小两个宝石的操作次数为 𝑚m，当我们删除两个最小的宝石时，剩下的宝石组成的数组就是从中删除了 2𝑚2m 个最小宝石和 (𝑘−𝑚)(k−m) 个最大宝石的宝石数组。

如何快速计算剩余元素的总和？首先，对原始数组进行排序不会影响结果，因为最小宝石始终在数组的开头，最大宝石则在数组的末尾。也就是排序后，每次操作要么删除左边的两个元素，要么删除右边的一个元素。因此，如果我们删除 2𝑚 个最小宝石和 (𝑘−𝑚) 个最大宝石，则剩余的元素组成的段在排序后的数组中从位置 (2𝑚+1) 到位置 (𝑛−(𝑘−𝑚)) ，可以从左到右遍历 m，使用前缀和在 O(1) 时间内计算其总和。总的时间复杂度 O(k)。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int main()
{int t;cin >> t;// 输入整数 t, 表示数据组数while (t--) {int n, k;cin >> n >> k;// 输入 n, 表示宝石的数量// 输入 k, 表示规定的处理次数vector<ll> a(n), prefix(n + 1, 0);// 数组 a 用来存储每个宝石的价值// prefix 用来存储前缀和, 初始化为 0for (int i = 0; i < n; i++) cin >> a[i];sort(a.begin(), a.end());// 排序宝石的价值for (int i = 1; i <= n; i++) prefix[i] = prefix[i - 1] + a[i - 1];// 计算前缀和, 用于快速计算任意区间宝石的总价值ll ans = 0;int pos = 0;// ans 最大化宝石价值// pos 表示当前考虑的宝石区间的起始位置while (k >= 0) {ans = max(ans, prefix[n - k] - prefix[pos]);// 从剩下的宝石中选择价值最大的 n-k 个宝石pos += 2; // 跳过两个宝石, 因为每次处理我们都是取一对宝石k--;}cout << ans << "\n";}return 0;
}

解法二：

#include <bits/stdc++.h>/*
前缀和。
求出前缀和后，枚举操作一的次数，即可获得当前的答案，取 max 即可。
时间复杂度 O(n)
*/// 排序后, 留下开的宝石一定是连续的一段
// 可以发现, 这连续的一段一共只有 k + 1 种
// 枚举删除最大的删除了多少个, 则立刻知道留下来的宝石是哪些
// 不能直接求和
// 前缀和可以解决using LL = long long;void solve(const int &Case) {int n, k;std::cin >> n >> k;std::vector<int> a(n);for (auto &x: a)std::cin >> x;std::sort(a.begin(), a.end());std::vector<LL> pre(n + 1); //注意long long for (int i = 1; i <= n; i++)pre[i] = pre[i - 1] + a[i - 1]; //求前缀和LL ans = 0;for (int i = 0; i <= k; i++) { // 枚举删除最小的操作用了几次// 设 i = 0, 可以发现留下来的是 1 2 3 ... n - k// 设 i = k, 可以发现留下来的是 2 * k ... n - 1ans = std::max(ans, pre[n - (k - i)] - pre[2 * i]);}std::cout << ans << '\n';
}//2 ^ 10 约等于 1000
//2 ^ 30 约等于 10^10
//计算机一秒跑 2 * 10^8int main() {std::ios::sync_with_stdio(false);std::cin.tie(nullptr);std::cout.tie(nullptr);int T = 1;std::cin >> T;for (int i = 1; i <= T; i++)solve(i);return 0;
}

今天就先到这了！！！