excel统计分析——拉丁方设计-编程知识

excel统计分析——拉丁方设计

参考资料：生物统计学

拉丁方设计也是随机区组设计，是对随机区组设计的一种改进。它在行的方向和列的方向都可以看成区组，因此能实现双向误差的控制。在一般的试验设计中，拉丁方常被看作双区组设计，用于提高发现处理效应差别的效率。

1、设计方法

拉丁方是指用字母排成一个阶方阵，使得每一行、每一列中每个字母都恰好各出现一次。拉丁方设计（Latin square design）就是利用拉丁方安排试验的试验设计，是一种二维设计，用于有三个因素而且每个因素的水平数都相同的研究。如果试验水平数为k，则共安排k^2个试验。

2、主要特点

（1）经济性：通过k的平方个试验完成三因素各k个水平的试验，非常节省试验单位数。如果要从试验中获取更多信息时，需要安排“重复拉丁方”试验，“重复”不是复制相同的拉丁方，而是采用同样大小而处理排列不同的拉丁方。

（2）匀称性：均匀性是拉丁方的另一个优点。虽然拉丁方只用一个二维的正方格子表示，但所研究的三个因素各处理在拉丁方中是均匀分布的。

3、试验结果的统计分析

拉丁方设计资料的统计分析采用无重复观测值的三因素方差分析模型。没有“重复拉丁方”时，只能分析各因素的主效应。由于各因素水平相同，只考虑主效应，数学模型为：

$x_{ijkl}=\mu+\alpha_i+\beta_j+\gamma _k+\varepsilon _{jikl}$

其中， $x_{ijkl}$ 为A因素i水平B因素j水平C因素k水平的第l个观测值； $\alpha_i$ 、 $\beta_j$ 、 $\gamma_k$ 为各因素的处理效应； $\varepsilon _{jikl}$ 为误差。平方和与自由度的分析如下：

$SS_T=\sum x^2-C$ ， $df_T=a^2-1$

$SS_A=\sum T_i^2/a-C$ ， $df_A=a-1$

$SS_B=\sum T_j^2/a-C$ ， $df_B=a-1$

$SS_C=\sum T_k^2/a-C$ ， $df_B=a-1$

$SS_e=SS_T-SS_A-SS_B-SS_C$ ， $df_e=(a-1)(a-2)$

其中，T为总变异，ABC为各因素的变异，e为误差；a为因素水平数；Ti为A因素i水平的观测值之和，Tj为B因素j水平的观测值之和，Tk为C因素k水平的观测值之和； $C=T^2/a^2$ ，T为所有观测值的总和。

4、拉丁方设计的变形

（1）不完全拉丁方设计

如果试验的某一因素与其他因素的水平数不同，这时拉丁方就不再是方阵而是一个矩阵，这时的拉丁方设计为不完全拉丁方设计（incomplete Latin square design）。不完全拉丁方设计资料的统计分析参考平衡不完全区组设计进行平方和分解，试验处理的平方和需要矫正，重复数、自由度参照公式据实计算。

（2）正交拉丁方设计

如果在拉丁方字母（数字）上在叠加一个希腊字母，并且限定每个拉丁字母与希腊字母只相遇一次，此时拉丁方为正交拉丁方。正交拉丁方（crossed Latin square design）即利用正交拉丁方安排试验的试验设计。正交拉丁方也是一个二维设计，但客供研究四个因素，但要求每个因素的水平数相同，是拉丁方设计的扩展，并以此可推广到更多因素的拉丁方设计。

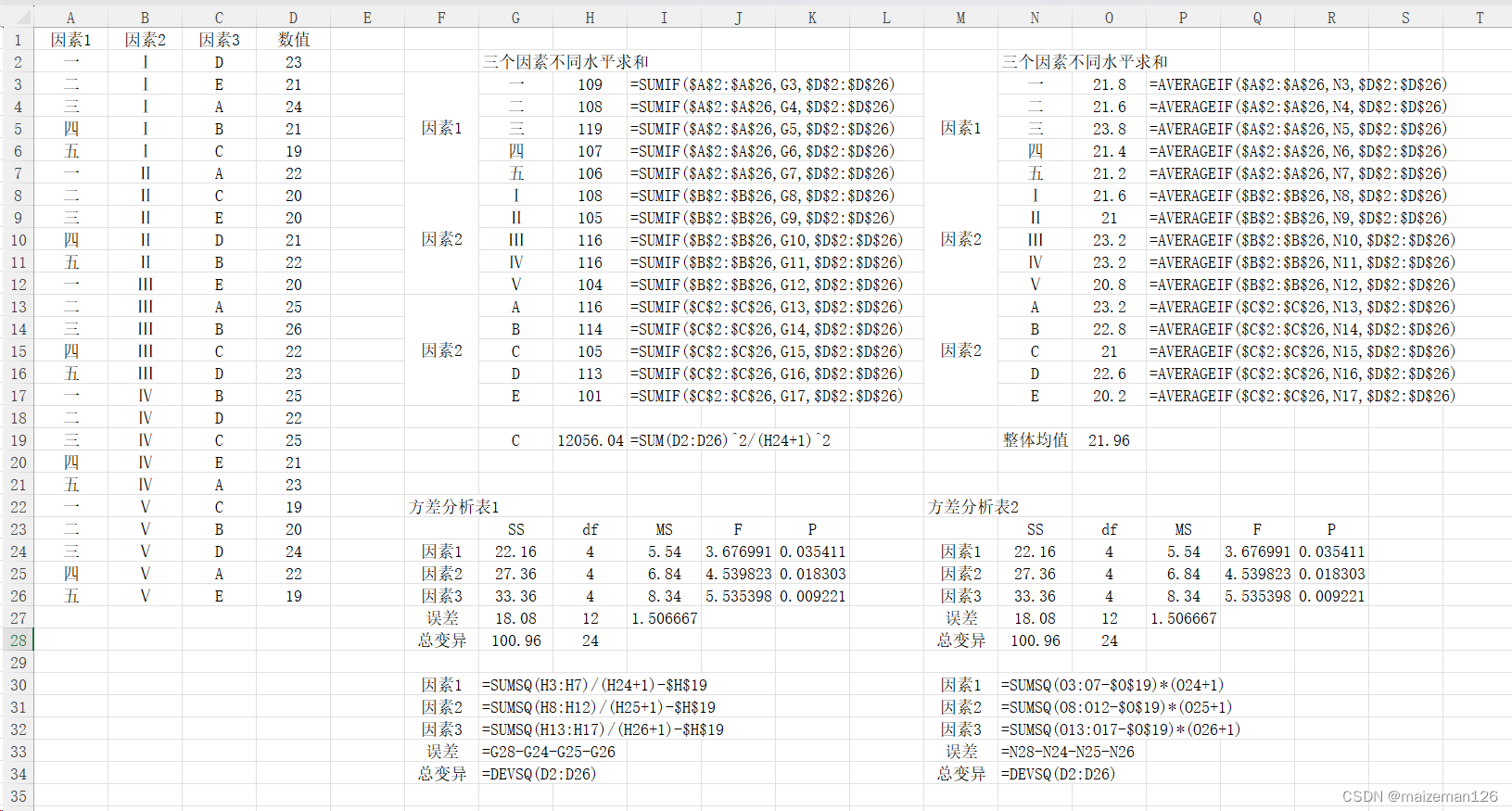
5、案例

因素1的5个水平：用一、二、三、四、五表示

因素2的5个水平：用Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ表示

因素3的5个水平：用A、B、C、D、E表示

方差分析过程如下：