算法的时间复杂度及空间复杂度-编程知识

算法的时间复杂度及空间复杂度

在这里插入图片描述

算法是指操作数据，解决问题的一组方法，就像排序一个无序数组使用不同的排序方法所耗费的时间和空间是不一样的，解决问题使用不同的算法耗费的时间和空间也会大有不同。
接下来我们就来详细了解一下时间复杂度和空间复杂度是如何去考量的。
算法的时间复杂度的考量我们虽然可以写一段程序去记录运行的时间，但这种方法必然是有很多弊端的，难以控制的误差，测试时使用的数据规模都会对结果产生很大的影响。
为了描述算法的时间和空间复杂度，首先我们要先了解[大O符号表示法]
在这种表示法中，不会精确计算某一过程运行的次数，因为CPU运行速度很快，这样去估计没有意义。
用一个例子表示

for (int i = 0; i < n; i++)
{cout<<"hello";cout<<"hi";
}

在这段代码中，假设第一行执行的时间颗粒为1，第二行代码循环n次，时间颗粒为n，第三段也一样，这样运行完所需要的时间颗粒为2n+1，在n趋近于无限大时，加上的1就几乎没有影响了，倍数二也没有很大影响了，我们就可以用大O表示法，时间复杂度为O(n)。
常见的时间复杂度有以下几种
常数级O(1)，不管代码执行多少行，只要是没有循环或循环次数是可数的，那么这段代码的时间复杂度就都是O(1)，消耗的时间不会随着某个变量的增长而增长，无论有几十万行代码，他的时间复杂度都为O(1)
例如：

for (int i = 0; i < n; i++)
{}

对数阶O(logn)
就像我们耳熟能详的有序数组寻找某个数的二分查找法，在每次查找的过程中都能排除一半，假设有n个数字，我们只需要log2ⁿ的时间就可以找到。通常省略下边的2，当然也可以是其他数字。
另一个例子

int i = 1;
while (i < n)
{i *= 2;
}

该例中i是以次方的速度接近于n的，只需要循环log2ⁿ次就结束循环。
线性阶O(n)。

for (int i = 0; i < n; i++)
{}

线性对数阶O(nlogn)。
上边两个相乘

for (int i = 0; i < n; i++)
{int j = 1;while (j < n){j *= 2;}
}

平方阶O(n²)。

for (int i = 0; i < n; i++)
{for (int j = 0; j < n; j++){//}
}

K次方阶O(n^k)。
从上到下时间复杂度越来越大，执行的效率当然也是越来越慢。
我们来看几道题目
在这里插入图片描述
这道题目选C，很明显，我们上边已经说过大O是一个渐进表示法，不会去精确表示运行次数。
D选项是正确的，在用大O表示法，我们通常考虑最坏的情况，例如在一个普通二叉搜索树中找某一数值，我们会考虑最坏的情况
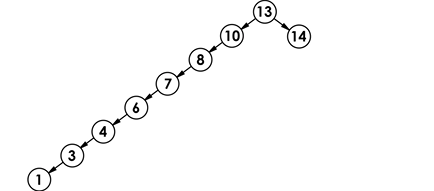
在这里插入图片描述
如上图，时间复杂度就会跌为O(n).
再来一题

这道题也是前边说过的，有两层循环，每层n次，时间复杂度为N*N，用大O表示法就是O(n²)次。

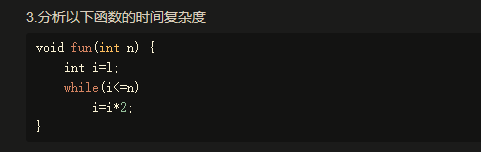
要注意，这里的i增长趋势是指数型的，所以这道题时间复杂度为O(logn)。
在这里插入图片描述
注意数组是有序的，我们可以设置两个指针分别指向首尾，根据这两个指针指向的数字和来判断移动，这道题目最坏的情况就是直到整个数组都被搜索一边，时间复杂度为O(n)。

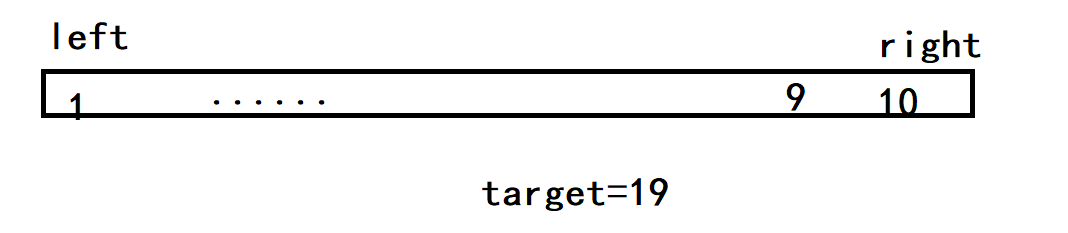
来一道编程题
消失的数字
这道题有很多种解法，需要在O(n)的时间内完成。
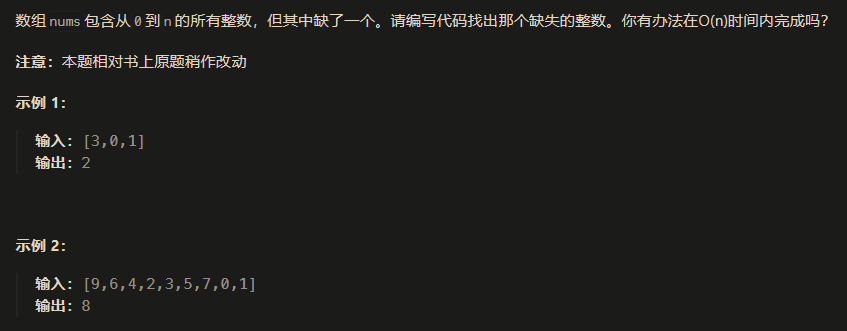
在这里插入图片描述
方法一：
可以新建一个数组，该数组包含从0到n，而且并没有缺少元素，我们可以通过将两个数组所有元素异或的方法找到该元素。
方法二：
很简单，求和公式，然后减去数组中所有元素，就可以得到缺失的整数。
以上方法的时间复杂度都为O(n)。
空间复杂度
我们已经知道了时间发咋读不是按照程序运行所消耗的时间来判定的，那么空间复杂度也不是用来计算程序实际占用的空间的。
空间复杂度是对一个算法在运行过程中临时占用存储空间大小的一个量度，同样梵音的是一个趋势。
空间复杂度比较常用的有O(1)，O(n)，O(n²)。
1，O（1）
入宫算法执行的时间复杂度不随着某个变量的大小而变化，那么该算法的空间复杂度就为O(1)。
2，O(n)

int* m = new int[n];
//

该行代码中，我们new出了一个数组，数组占用大小为n，此时他的空间复杂度就为O(N)，当然，类比一下，如果我们开辟了两个大小为n的数组呢？他的空间复杂度还是O(N)，因为当N趋近于无穷大时，他的倍数忽略也可。
我们来看一道题目
在这里插入图片描述
只要上边理解了，这里也就能很快得出答案，该二维数组的空间大小是一定的，不会变化，所以空间复杂度自然而然就为O(1).

这道题首先创作了一个指针数组，数组的大小为n，在下边的循环中，指针数组中n个指针分别指向一块空间大小为n的数组，我们可以将它们看作是一个正方形的二维数组，边长为n，所以则道题的空间复杂度为O(n²)。
总结
时间复杂度和空间复杂度是抽象出来用来形容一个算法的优略的，该文只是对两种概念进行解释，在后续的学习中很多地方会用到时间复杂度和空间复杂度用来判断一些算法的优略，希望我们能在学习中一起成长！