树桩数组

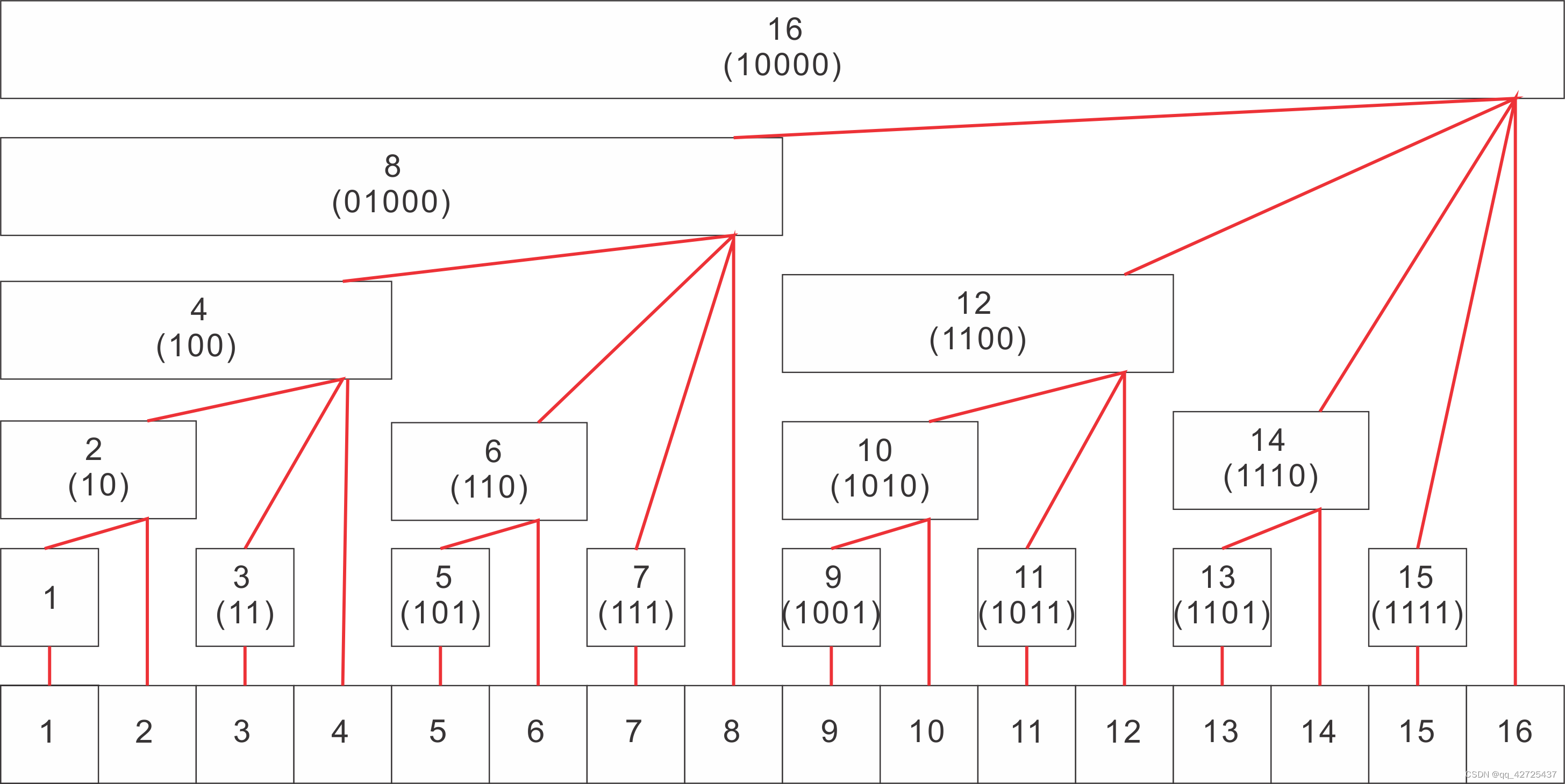
应用

• 单点修改、区间查询
• 区间修改、单点查询

单点修改、区间查询

找到当前节点的父亲节点：i += i&（-i），修改数组的值

def add(self, i: int) -> None:while i < len(self.tree):self.tree[i] += 1i += i & -i

查询在区间[1, i]的加和

def pre(self, i: int)->int:res = 0while i > 0:res += self.tree[i]i &= i-1return res

或者

def pre(self, i: int)->int:res = 0while i > 0:res += self.tree[i]i -= i & (-i) return res

区间修改、单点查询

对于区间修改的话，我们只需要对差分数组进行操作即可，例如对区间[L,R]+k,那么我们只需要更新差分数组add(L,k),add(R+1,-k)，这是差分数组的性质.
对于单点查询操作，求出b数组的前缀和即可，因为a[x]=差分数组b[1]+b[2]+…+b[x]的前缀和，这是差分数组的性质之一.