概述

本文介绍通过g2o框架，优化点和曲线的匹配（曲线拟合）。曲线的公式如下所示：

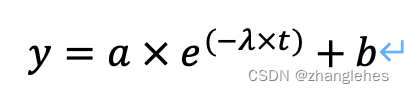
它有三个参数：a, b, lamba。

代码解析

自定义顶点

/*** \brief the params, a, b, and lambda for a * exp(-lambda * t) + b*/
class VertexParams : public g2o::BaseVertex<3, Eigen::Vector3d> { // 它包含三个参数public:EIGEN_MAKE_ALIGNED_OPERATOR_NEW;VertexParams() {}bool read(std::istream& /*is*/) override { return false; }bool write(std::ostream& /*os*/) const override { return false; }void setToOriginImpl() override {} // 设定参数的原始值void oplusImpl(const double* update) override { // 增量更新函数，调整当前参数的值Eigen::Vector3d::ConstMapType v(update); // 构造参数增量_estimate += v;}
};

自定义边

/*** \brief measurement for a point on the curve** Here the measurement is the point which is lies on the curve.* The error function computes the difference between the curve* and the point.*/
class EdgePointOnCurve: public g2o::BaseUnaryEdge<1, Eigen::Vector2d, VertexParams> { // 一条边只含有一个顶点，使用上面定义顶点的数据结构public:EIGEN_MAKE_ALIGNED_OPERATOR_NEWEdgePointOnCurve() {}bool read(std::istream& /*is*/) override {cerr << __PRETTY_FUNCTION__ << " not implemented yet" << endl;return false;}bool write(std::ostream& /*os*/) const override {cerr << __PRETTY_FUNCTION__ << " not implemented yet" << endl;return false;}template <typename T>bool operator()(const T* params, T* error) const { // 误差函数const T& a = params[0];const T& b = params[1];const T& lambda = params[2];T fval = a * exp(-lambda * T(measurement()(0))) + b; // 计算理论值error[0] = fval - measurement()(1); // 和观察值进行比较return true;}G2O_MAKE_AUTO_AD_FUNCTIONS  // use autodiff
};

生成待拟合的点

  // generate random datag2o::Sampler::seedRand();double a = 2.;double b = 0.4;double lambda = 0.2;Eigen::Vector2d* points = new Eigen::Vector2d[numPoints];for (int i = 0; i < numPoints; ++i) {double x = g2o::Sampler::uniformRand(0, 10);double y = a * exp(-lambda * x) + b;// add Gaussian noisey += g2o::Sampler::gaussRand(0, 0.02);points[i].x() = x;points[i].y() = y;}

初始化求解器

  // setup the solverg2o::SparseOptimizer optimizer;optimizer.setVerbose(false);// allocate the solverg2o::OptimizationAlgorithmProperty solverProperty;optimizer.setAlgorithm(g2o::OptimizationAlgorithmFactory::instance()->construct("lm_dense",solverProperty));

添加顶点

在本示例中，只存在一个顶点，就是待优化的参数

  // 1. add the parameter vertexVertexParams* params = new VertexParams();params->setId(0);params->setEstimate(Eigen::Vector3d(1, 1, 1));  // 参数的初始化值optimizer.addVertex(params);

添加边

在本示例中，每一个待拟合点，都对应一条边。也就是一个观察点就是一个观测值。

  // 2. add the points we measured to be on the curvefor (int i = 0; i < numPoints; ++i) {EdgePointOnCurve* e = new EdgePointOnCurve;e->setInformation(Eigen::Matrix<double, 1, 1>::Identity());e->setVertex(0, params);e->setMeasurement(points[i]);optimizer.addEdge(e);}

求解器求解

  optimizer.initializeOptimization();optimizer.setVerbose(verbose);optimizer.optimize(maxIterations); // 最大的迭代次数

结果展示

  // print out the resultcout << "Target curve" << endl;cout << "a * exp(-lambda * x) + b" << endl;cout << "Iterative least squares solution" << endl;cout << "a      = " << params->estimate()(0) << endl;cout << "b      = " << params->estimate()(1) << endl;cout << "lambda = " << params->estimate()(2) << endl;cout << endl;