20. 有效的括号 - 力扣（LeetCode）

这道题我们乍一看可能会选择暴力遍历法,但这题我们可以选择栈,这样可以大大降低我们的时间复杂度.这题要求非常简单

1. 左括号必须用相同类型的右括号闭合。
2. 左括号必须以正确的顺序闭合。
3. 每个右括号都有一个对应的相同类型的左括号。

所以我们可以这样想,创建一个栈,当我们获得一个左括号时,我们将其放入栈,然后等出现右括号时,与左括号比较,如果不匹配就返回false,匹配就将这个符号出栈.反正我们只要记住,后出现的左括号要先与右括号匹配,总结括号的匹配具有就近原则,

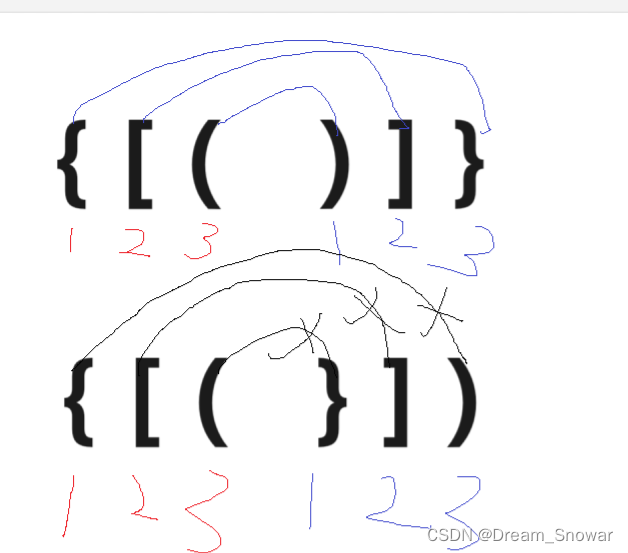
那么我们就可以尝试实现代码了,但其实有一种情况,我们不需要遍历就能知道括号不匹配,那么是什么情况呢?

就是所给的数组元素个数为奇数时(所给条件中S>=1所以S=0不考虑)

我们知道S是个字符串数组,所以我们可以直接调用strlen函数求出字符个数,然后与2取模如果结果为1则返回false

  int n=strlen(s);if(n%2==1){return false;}

接着我们开始创建栈,然后然后我们需要将数据导入栈了!

但是我们该如何将栈中存储的左括号和右括号配对呢?

这里我选择自己定义一个函数:

char pairs(char a) 
{if (a == '}') return '{';if (a == ']') return '[';if (a == ')') return '(';return 0;
}

如果检测到左括号则返回相应右括号,这样之后我们只需要让出现的右括号和栈顶的右括号比较就可以知道是否匹配了.

接着我们完成栈和判断

    int stk[n + 1], top = 0;for (int i = 0; i < n; i++){char ch = pairs(s[i]);if (ch){if (top == 0 || stk[top - 1] != ch) {return false;}top--;}else {stk[top++] = s[i];}}return top == 0;

最后结果是:

 

char pairs(char a) 
{if (a == '}') return '{';if (a == ']') return '[';if (a == ')') return '(';return 0;
}
bool isValid(char* s)
{int n=strlen(s);if(n%2==1){return false;}int stk[n + 1], top = 0;for (int i = 0; i < n; i++){char ch = pairs(s[i]);if (ch){if (top == 0 || stk[top - 1] != ch) {return false;}top--;}else {stk[top++] = s[i];}}return top == 0;
}