激光雷达点云数据邻域特征计算理论知识学习-编程知识

一、数学理论

（一）SVD奇异值分解（Singular value decomposition）

奇异值分解是线性代数中一种重要的矩阵分解，在信号处理、统计学等领域有重要应用。奇异值分解在某些方面与对称矩阵或埃尔米特矩阵基于特征向量的对角化类似。然而这两种矩阵分解尽管有其相关性，但还是有明显的不同。对称阵特征向量分解的基础是谱分析，而奇异值分解则是谱分析理论在任意矩阵上的推广[2]。

假设M是一个m×n阶矩阵，其中的元素全部属于域K，也就是实数域或复数域。如此则存在一个分解使得

$M=U\Sigma V^{*}$

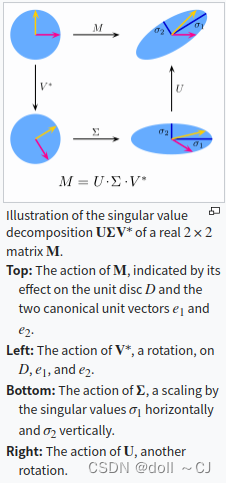
其中U是m×m阶酉矩阵（其共轭转置恰为其逆矩阵的复数方阵），Σ是m×n阶非负实数对角矩阵，而V*则为V的共轭转置，是n×n阶酉矩阵。这样的分解就称作M的奇异值分解。Σ对角线上的元素Σi,i即为M的奇异值。常见的做法是将奇异值由大而小排列，如此Σ便能由M唯一确定了（虽然U和V仍然不能确定）[2]。

奇异值分解的应用有（包括但不限于下述应用）[2]：

1、用来计算矩阵的广义逆阵（伪逆）；

2、给出矩阵的列空间、零空间和秩的表示。对角矩阵 $\Sigma$ 的非零对角元素的个数对应于矩阵M的秩。与零奇异值对应的右奇异向量生成矩阵M的零空间，与非零奇异值对应的左奇异向量则生成矩阵M的列空间。在线性代数数值计算中，奇异值分解一般用于确定矩阵的有效秩，这是因为，由于舍入误差，秩亏矩阵的零奇异值可能会表现为很接近零的非零值；

3、在统计中的主要应用为主成分分析（PCA）。数据集的特征值（在SVD中用奇异值表征）按照重要性排列，降维的过程就是舍弃不重要的特征向量的过程，而剩下的特征向量张成空间为降维后的空间。实际上，SVD在PCA降维上只是使用了右奇异矩阵V，因为右奇异阵V是进行列压缩[3]。

（二）埃尔米特矩阵（Hermitian matrix）

埃尔米特矩阵（又称厄米特矩阵、厄米矩阵及自伴随矩阵），是共轭对称的方阵，其每一个第i行第j列的元素都与第j行第i列的元素复共轭（在数学中，复数的共轭复数就是对虚部变号的运算）且主对角线元素必须为实数。埃尔米特矩阵可以理解为实对称矩阵的复数扩展，查尔斯·埃尔米特于1855年证明了埃尔米特矩阵和实对称矩阵有一个共同的性质，即总存在实特征值[4]。

埃尔米特矩阵的应用有（包括但不限于下述应用）[4]：

1、在信号处理中，厄米矩阵被用于傅里叶分析和信号表示等任务。厄米矩阵的特征值和特征向量在分析信号和提取有意义的信息中起着至关重要的作用；

2、厄米矩阵在线性代数和数值分析中得到了广泛的研究，它们具有良好定义的光谱特性，许多数值算法，如Lanczos算法，利用这些特性进行高效计算。厄米矩阵也出现在奇异值分解(SVD)和特征值分解等技术中；

3、在统计学和机器学习中，厄米矩阵用于协方差矩阵，它们表示不同变量之间的关系。厄米协方差矩阵的正定性保证了多元分布的良好定义性。

（三）实对称矩阵（Real symmetric matrix）

在线性代数中，实对称阵指的是元素均为实数且转置矩阵和自身相等的方形矩阵。实对称矩阵的不同特征值所对应的特征向量是正交的；实对称矩阵的特征值都是实数，特征向量都是实向量；n阶实对称矩阵必可利用正交矩阵对角化[5]。

（四）协方差矩阵（Covariance matrix）

在统计学与概率论中，协方差矩阵是一个方阵，代表着任两列随机变量间的协方差，是协方差的直接推广。协方差矩阵是很多领域里非常有力的工具，其能导出一个变换矩阵，这个矩阵能使数据完全去相关，也可以说能够找到一组最佳的基来紧凑地表达数据（瑞利商证明）。这个方法在统计学中被称为主成分分析，在图像处理中被称为K-L变换[6]。

此处提供一个瑞利商寻求最佳基的使用例子，详见博客Fisher线性判别实践。