逻辑斯蒂回归解决的事分类问题，分类输出的是类别的概率

模型

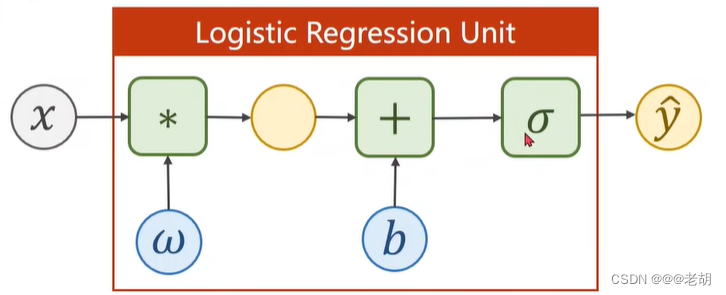
在线性模型中，通过$y=wx+b$输出的是一个实数值，但是在分类问题中，输出的是类别的概率，所以需要一个函数，把实数值映射到[0,1]之间，表示概率，这个函数为 sigmoid 函数$y=\frac{1}{1+e^{-x}}\in [0,1]$，sigmoid函数属于饱和函数。

以上，逻辑斯蒂回归模型的公式为：$\hat{y}=\sigma (x\ast w+b)$

损失函数

在线性回归中，计算损失一般是使用均方误差(预测值与真实值的差值的平方和的累加)，在回归问题中，均方误差表示数轴上两个值之间的距离，但是分类问题中，输出的结果表示的是概率（分布），使用距离是没有意义的，所以分类问题中的损失函数并不是均方误差。

在逻辑斯蒂回归中，使用的是BCE

代码和结果

import torch
import torch.nn.functional as F
import numpy as np
import matplotlib.pyplot as pltx_data=torch.Tensor([[1.0],[2.0],[3.0]])
y_data=torch.Tensor([[0],[0],[1]])class LogisticRegressionModel(torch.nn.Module):def __init__(self):super(LogisticRegressionModel,self).__init__()self.linear=torch.nn.Linear(1,1)def forward(self,x):y_pred=F.sigmoid(self.linear(x))return y_predmodel=LogisticRegressionModel()# 损失函数
criterion=torch.nn.BCELoss(size_average=False)
# 优化器
optimizer=torch.optim.SGD(model.parameters(),lr=0.01)# 训练
for epoch in range(1000):y_pred=model(x_data)loss=criterion(y_pred,y_data)print(epoch,loss.item())optimizer.zero_grad()loss.backward()optimizer.step()# linspace与range函数类似，用于生成均匀分布的数值序列
# np.linspace(start=0,stop=10,num=200)
x=np.linspace(0,10,200)
# 数据集，test，生成200*1的矩阵
x_t=torch.Tensor(x).view((200,1))
y_t=model(x_t)
y=y_t.data.numpy()
plt.plot(x,y)
plt.plot([0,10],[0.5,0.5],c='r')
plt.xlabel("Hours")
plt.ylabel("Probability of Pass")
# 显示网格线
plt.grid()
plt.show()