红黑树（Red-Black Tree）是一种自平衡的二叉搜索树，它在插入和删除节点时通过一系列的旋转和重新着色操作来保持平衡。红黑树的平衡性质使得它的查找、插入和删除操作的时间复杂度都能保持在 O(log n)

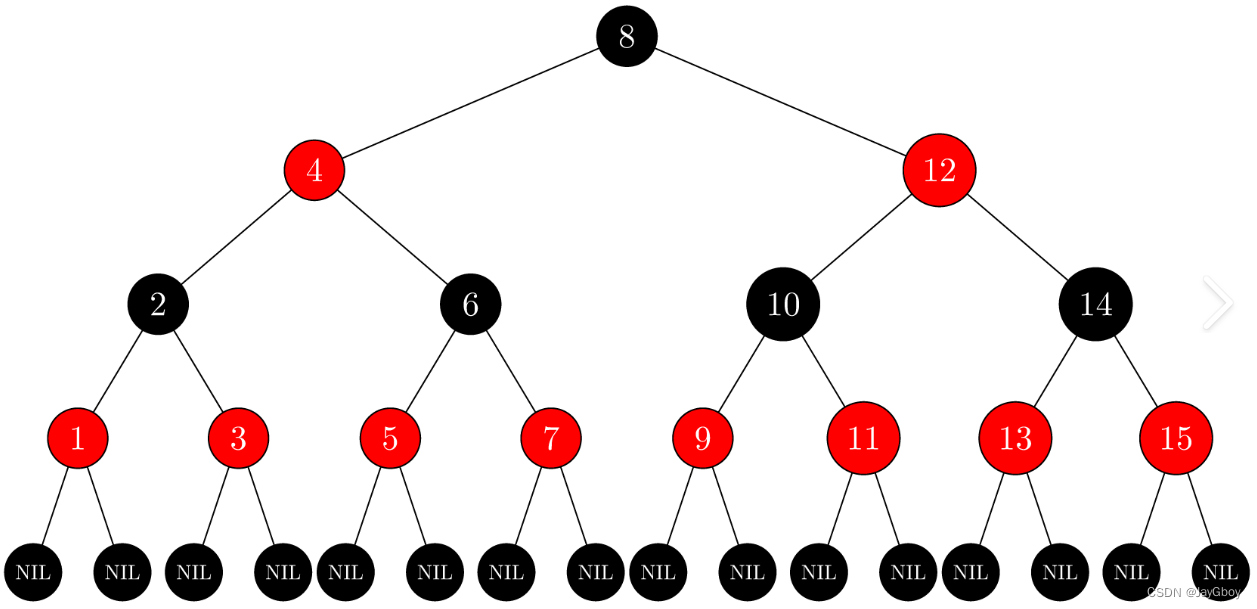
红黑树的定义如下：

1. 每个节点要么是红色，要么是黑色。
2. 根节点是黑色的。
3. 每个叶子节点（NIL节点，即空节点）是黑色的。
4. 如果一个节点是红色的，则它的两个子节点都是黑色的。
5. 对于每个节点，从该节点到其所有后代叶子节点的简单路径上，均包含相同数目的黑色节点。

下面是一个简单的红黑树的实现示例（使用Python语言）：

# 定义红黑树节点类
class Node:def __init__(self, key):self.key = keyself.left = Noneself.right = Noneself.parent = Noneself.color = 1  # 1表示红色，0表示黑色# 定义红黑树类
class RedBlackTree:def __init__(self):self.NIL = Node(None)  # 空节点self.root = self.NIL# 左旋操作def left_rotate(self, x):y = x.rightx.right = y.leftif y.left != self.NIL:y.left.parent = xy.parent = x.parentif x.parent == self.NIL:self.root = yelif x == x.parent.left:x.parent.left = yelse:x.parent.right = yy.left = xx.parent = y# 右旋操作def right_rotate(self, x):y = x.leftx.left = y.rightif y.right != self.NIL:y.right.parent = xy.parent = x.parentif x.parent == self.NIL:self.root = yelif x == x.parent.left:x.parent.left = yelse:x.parent.right = yy.right = xx.parent = y# 插入节点def insert(self, key):node = Node(key)node.parent = self.NILnode.left = self.NILnode.right = self.NILnode.color = 1  # 新插入的节点为红色y = Nonex = self.rootwhile x != self.NIL:y = xif node.key < x.key:x = x.leftelse:x = x.rightnode.parent = yif y == None:self.root = nodeelif node.key < y.key:y.left = nodeelse:y.right = nodeif node.parent == None:node.color = 0  # 如果插入的是根节点，则将其颜色设置为黑色returnif node.parent.parent == None:returnself.insert_fixup(node)# 插入修复操作def insert_fixup(self, node):while node.parent.color == 1:if node.parent == node.parent.parent.right:y = node.parent.parent.leftif y.color == 1:node.parent.color = 0y.color = 0node.parent.parent.color = 1node = node.parent.parentelse:if node == node.parent.left:node = node.parentself.right_rotate(node)node.parent.color = 0node.parent.parent.color = 1self.left_rotate(node.parent.parent)else:y = node.parent.parent.rightif y.color == 1:node.parent.color = 0y.color = 0node.parent.parent.color = 1node = node.parent.parentelse:if node == node.parent.right:node = node.parentself.left_rotate(node)node.parent.color = 0node.parent.parent.color = 1self.right_rotate(node.parent.parent)if node == self.root:breakself.root.color = 0# 中序遍历红黑树def inorder(self, node):if node != self.NIL:self.inorder(node.left)print(node.key, end=" ")self.inorder(node.right)# 测试红黑树
tree = RedBlackTree()
tree.insert(10)
tree.insert(20)
tree.insert(30)
tree.insert(40)
tree.insert(50)
tree.insert(60)
tree.insert(70)
tree.insert(80)
tree.inorder(tree.root)

红黑树作为一种自平衡的二叉搜索树，具有以下优点和缺点：

优点：

1. 平衡性：红黑树通过旋转和重新着色操作来保持树的平衡，使得树的高度相对较低，从而保证了查找、插入和删除操作的时间复杂度为 O(logn)，在最坏情况下也能保证 O(logn) 的性能。
2. 高效的插入和删除操作：红黑树的插入和删除操作相对较快，因为它能够通过旋转和重新着色来保持树的平衡，而不需要像平衡二叉搜索树那样频繁地进行调整。
3. 适用于高效的查找操作：红黑树是一种二叉搜索树，因此可以进行高效的查找操作。它可以快速定位到目标节点，并且具有较好的平均性能。

缺点：

1. 相对复杂：相比于其他简单的数据结构，红黑树的实现相对复杂，需要处理旋转和重新着色等操作，因此实现起来可能会比较困难和容易出错。
2. 额外的存储空间：为了维护红黑树的平衡性，每个节点需要额外存储一个颜色标记，这会占用额外的存储空间。
3. 不适合频繁的插入和删除操作：虽然红黑树的插入和删除操作相对较快，但是频繁的插入和删除操作会导致频繁的平衡调整，影响性能。如果应用场景需要频繁地插入和删除节点，可能会有更适合的数据结构选择。

红黑树在平衡性和高效的查找、插入和删除操作方面具有优势，但相对复杂，需要额外的存储空间，并且不适合频繁的插入和删除操作。