高级数据结构
1. 概念
之所以称它们为高级的数据结构,是因为它们的实现要比那些常用的数据结构要复杂很多,能够让我们在处理复杂问题的过程中,
多拥有一把利器,同时掌握好它们的性质,以及所适应的场合,在分析问题的时候回归本质,那么很多问题都能迎刃而解了。
2. 总结
1> 前缀树
| 题目 | 说明 | 实现 |
|---|---|---|
| 1268. 搜索推荐系统 | 一眼前缀树 | 我的提交 |
| 1233. 删除子文件夹 | 使用哈希表存储子前缀树,ref存储在列表中的位置 | 我的提交 |
| 140. 单词拆分 II | 前缀树 | 我的提交 |
| 212. 单词搜索 II | 对已搜索到的单词剪去,大大降低搜索时间 | 我的提交 |
| 648. 单词替换 | 前缀树 | 我的提交 |
2> 树状数组
①普通
②离散化
| 题目 | 说明 | 实现 |
|---|---|---|
| 315. 计算右侧小于当前元素的个数 | 前缀和 | 我的提交 |
| 2250. 统计包含每个点的矩形数目 | 前缀和 | 我的提交 |
| 775. 全局倒置与局部倒置 | 前缀和 | 我的提交 |
| 327. 区间和的个数 | 记录前缀和,每个i结尾的合法区间数 = 特定区间内前缀和的的数目,数据太大所以预处理离散化 | 我的提交 |
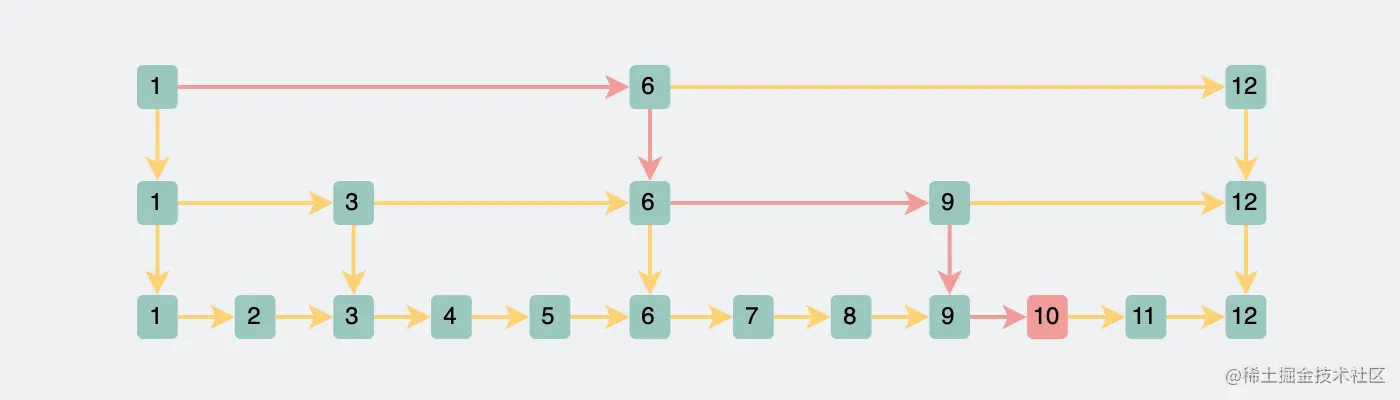
3> 跳表
原理:将部分链表结点提出来,再构建出一个新的链表,跳表使用空间换时间的设计思路,通过构建多级索引来提高查询的效率,实现了基于链表的“二分查找”。跳表是一种动态数据结构,支持快速地插入、删除、查找操作,时间复杂度都是 O(logn)。
查询:要查询一个数据的时候,我先查上层的链表,就很容易知道数据落在哪个范围,然后跳到下一个层级里进行递归查询
**插入:**需要某种手段来维护索引与原始链表大小之间的平衡,因此在插入时可以选择同时将这个数据插入到部分索引层中。而我们通过一个随机函数,来决定将这个结点插入到哪几级索引中
**删除:**删除原链表中的节点,如果节点存在于索引中,也要删除索引中的节点,如果在删除操作后某些层变得空了(即除了头节点外没有其他节点),那么需要减少跳表的高度并移除这些空的层。
4> LRU缓存
## LRU
LRU 是 Least Recently Used 的缩写,即最近最少使用,是一种常见的页面置换算法。LRU 算法的基本理念是:最近使用的数据在未来一段时间仍会被使用,
已经很久没有使用的数据可能在未来较长的一段时间内不会被使用。所以在需要淘汰页面时,每次选择淘汰最久没有被访问的页面。
## 数据结构
通过 golang 内置的双向链表 list.List 存储每个节点,同时维护一个哈希表,可快速判断需要加载的数据是否已经在链表中存在,无须遍历链表查找,典型
的以空间换时间的方式。
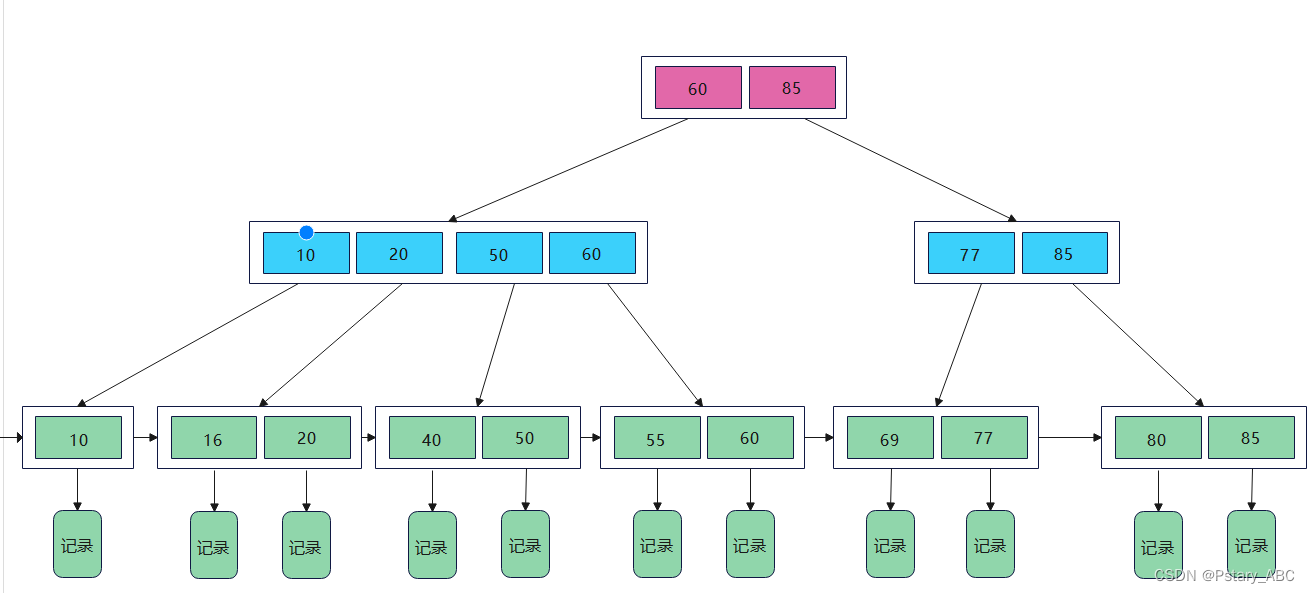
5> B+树
每个分支节点最多有m棵子树(孩子节点);
非叶根节点至少有两棵子树,其他每个分支节点至少有⌈m/2⌉棵子树;
节点的字数个数与关键字个数相等;
所有叶节点包含全部关键字及指向相应记录的指针,叶节点中将关键字按大小顺序排列,并且相邻叶节点按大小顺序相互链接起来;
所有分支节点(可视为索引的索引)中仅包含他的各个子节点(即下一级的索引块)中关键字的最大值及指向其子节点的指针。
6> 红黑树
是一种自平衡的二叉搜索树,它在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出两倍(因此红黑树的平衡性要求相对宽松),从而使搜索树达到一种相对平衡的状态。
性质:
根结点必须是黑色的 每个叶子结点都是黑色的(此处的叶子结点指的是空结点,也被称为NIL节点) 红色结点的两个子结点必须都是黑色的,这保证了没有两个连续的红色节点相连 任意结点到其每个叶子结点的简单路径上,黑色节点的数量相同:确保了树的黑平衡性,即红黑树中每条路径上黑色结点的数量一致。实现:
const (RED = trueBLACK = false ) type Node struct {Parent *NodeLeft *NodeRight *Nodecolor boolItem }
- 为什么最长路径是最短的两倍?
如果有一条全黑的路径,那这条全黑的路径一定就是最短路径;如果有一条是严格黑红相间的,那他就是最长的路径。 然后它们里面的黑色结点个数又是相同的的,所以最长路径最多是最短路径的两倍,不可能超过最短路径两倍。
- 每个叶子结点都是黑色的(此处的叶子结点指的是空结点,也被称为NIL节点),有什么用?
为了更好的帮我们区分不同路径的,如果不带空的话,我们可能会认为有5条,但是这里计算路径其实应该走到空(NIL),所以正确的应该是有11条路径。
- 为什么不用AVL树要用红黑数?
红黑树的查找效率是比不上AVL树的,最大为2logn(但对于计算机来说是没什么差别的,因为它们是同一个数量级的)
但是,由于AVL树要求更加严格的平衡,所以在进行插入和删除操作时,可能需要更频繁地进行旋转操作来调整树的结构,以保持平衡。相比之下,红黑树的插入和删除操作需要旋转的次数相对较少,因此在插入和删除操作频繁的情况下,红黑树可能更加高效。
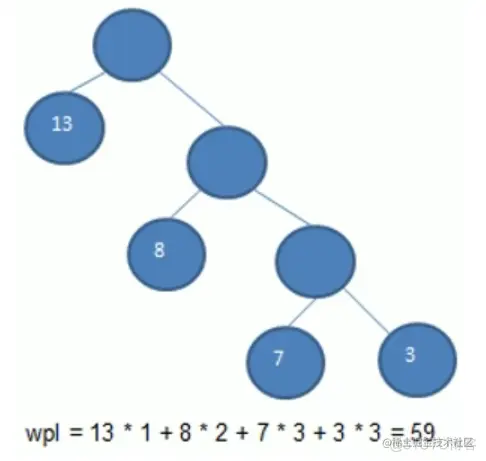
7> 哈夫曼树
给定n个权值作为个叶子结点,构造一棵二叉树,若该树的带权路径长度(wpl)达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树Huffman Tree,还有的书翻译为霍夫曼树。
赫夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
1)从小到大进行排序,每个节点可以看成是一颗最简单的二叉树,得到一个森林
2)取出根节点权值最小的两颗二叉树
3)组成一颗新的二叉树,该新的二叉树的根节点的权值是前面两颗二叉树根节点权值的和,删除原来两颗二叉树,将这颗新的二叉树加入森林
4)再次排序,不断重复1-2-3-4的步骤,直到数列中,所有的数据都被处理,就得到一颗哈夫曼树
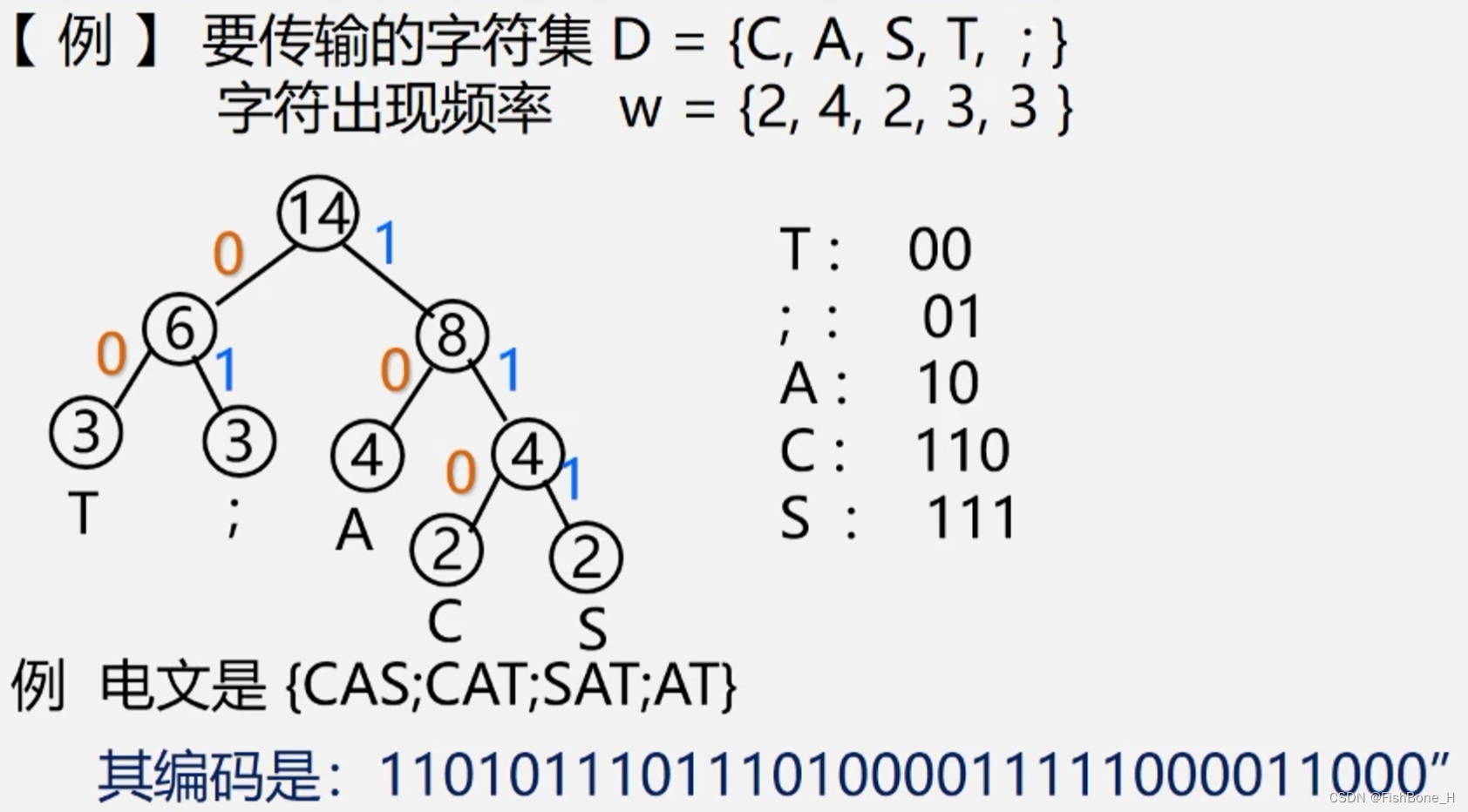
哈夫曼编码
要设计长度不等的编码,则必须使任一字符的编码都不是另一字符编码的前缀(称为前缀编码)统计字符集中每个字符在电文中出现的平均频率(概率越大,要求编码越短)。
利用哈夫曼树的特点:权越大的叶子离根越近;将每个字符的概率值作为权值,构造哈夫曼树。
在哈夫曼树的每个分支上标0或1:结点的左分支标0,有右分支标1。
把从根到每个叶子的路径上的标号连接起来,作为该叶子代表的字符的编码。
3. 更多练习
4. 参考
- 哈夫曼树&哈夫曼编码
- B+树
- 总库:tryHard