【Python】使用numpy进行神经网络激活函数算法描述
系统:macOS 10.14.5 IDE:PyCharm 2018.2.4
一、What
1.1 NumPy
NumPy(Numerical Python) 是 Python 语言的一个扩展程序库,支持大量的维度数组与矩阵运算,此外也针对数组运算提供大量的数学函数库。 NumPy 的前身 Numeric 最早是由 Jim Hugunin 与其它协作者共同开发,2005 年,Travis Oliphant 在 Numeric 中结合了另一个同性质的程序库 Numarray 的特色,并加入了其它扩展而开发了 NumPy。NumPy 为开放源代码并且由许多协作者共同维护开发。 NumPy 是一个运行速度非常快的数学库,主要用于数组计算,包含:
- 一个强大的N维数组对象 ndarray
- 广播功能函数
- 整合 C/C++/Fortran 代码的工具
- 线性代数、傅里叶变换、随机数生成等功能
1.2 激活函数
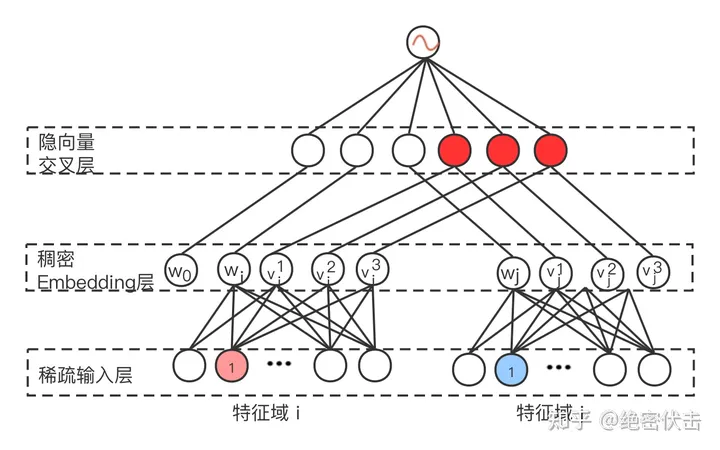
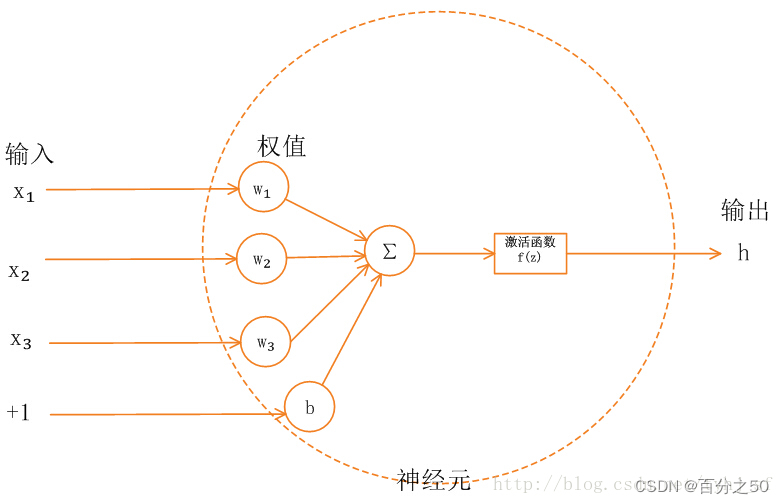
神经网络中的每个神经元节点接受上一层神经元的输出值作为本神经元的输入值,并将输入值传递给下一层,输入层神经元节点会将输入属性值直接传递给下一层(隐层或输出层)。在多层神经网络中,上层节点的输出和下层节点的输入之间具有一个函数关系,这个函数称为激活函数(又称激励函数)。
二、Why
最近接触了一些AI的知识点,感觉Python在这方面还是很有优势的,特别是库的应用,很多精彩的算法公式都可以通过Python简洁的表达出来,主要是numpy,提供了大量数学工具,在激活函数中描述相关的表达式非常方便。
三、How
3.1 准备工作
3.1.1 安装numpy和matplotlib
1、打开偏好设置

2、选择工程文件,选择Project Interpreter,点击+号
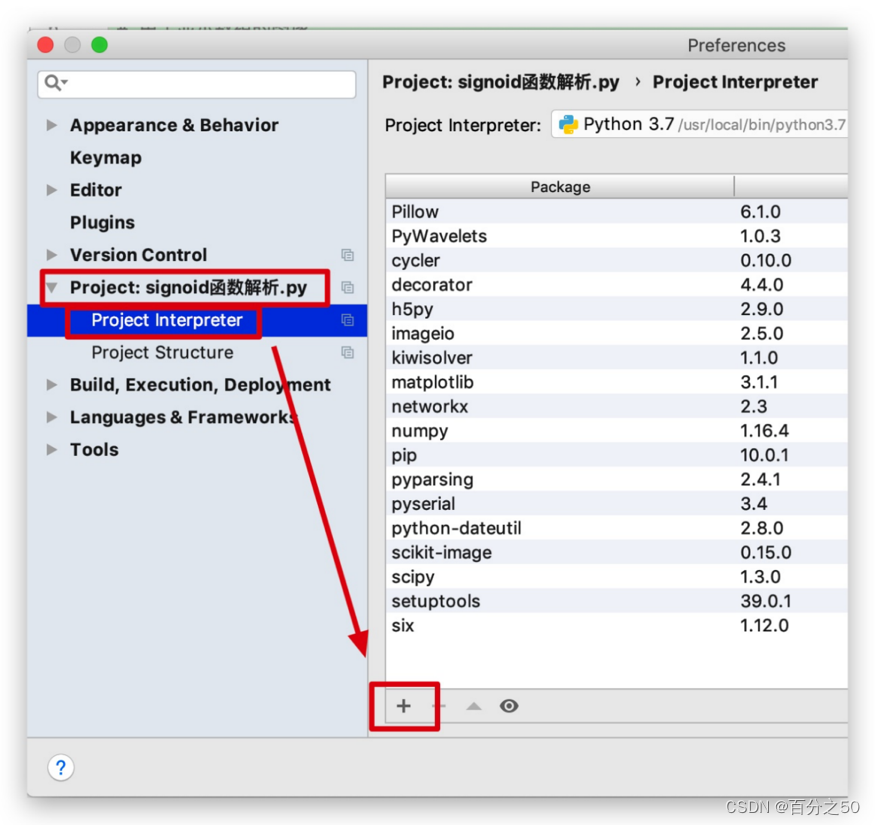
3、搜索numpy,点击Install Package
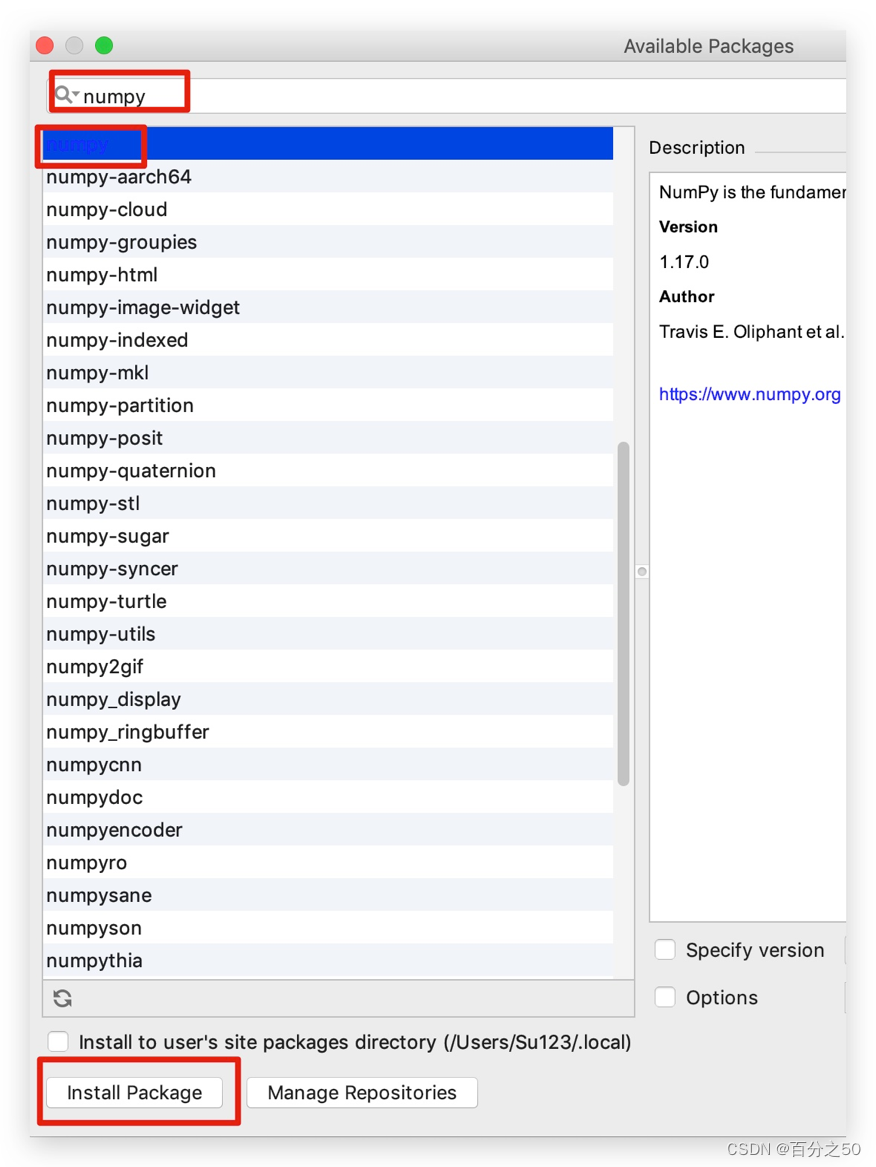
4、稍等片刻,IDE底部会有状态条提示,安装成功后出现如下提示
5、用同样的方式安装matplotlib 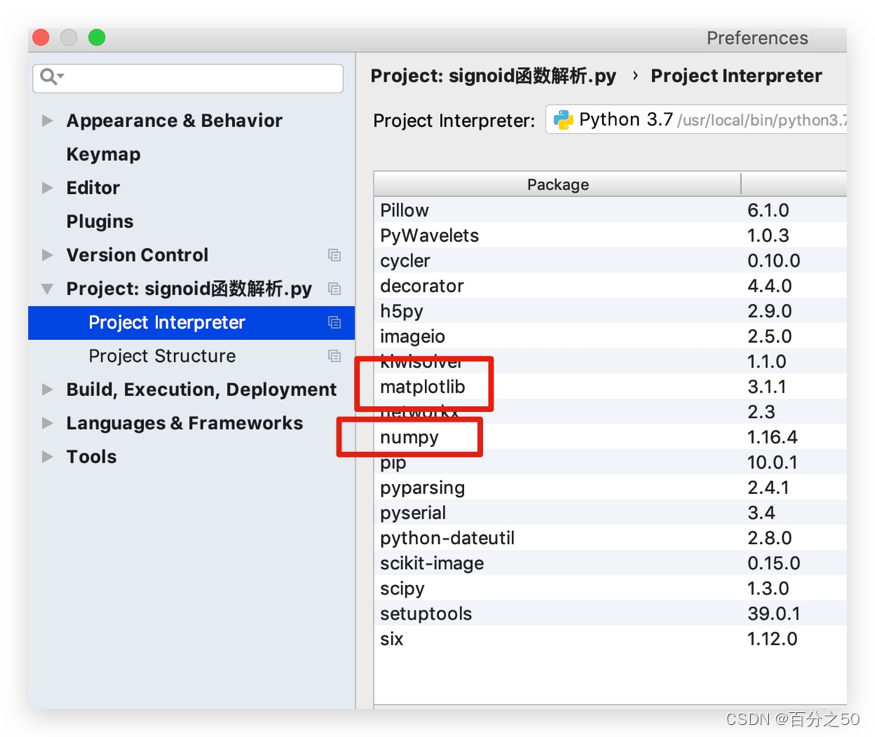
6、然后回到代码中检查是否能import 
import numpy as npimport matplotlib.pyplot as plt没有标红即正常,as表示给这个库命名,把上面的两个库命名为np和plt是目前通用做法,matplotlib.pyplot主要是用来画图,后面我们会用它来绘制函数的曲线。
3.2 基础数组与画图操作
3.2.1 生成数组
首先我们用numpy生成一个数组,使用arange函数直接生成一维数组,传入一个整数说明数组的长度 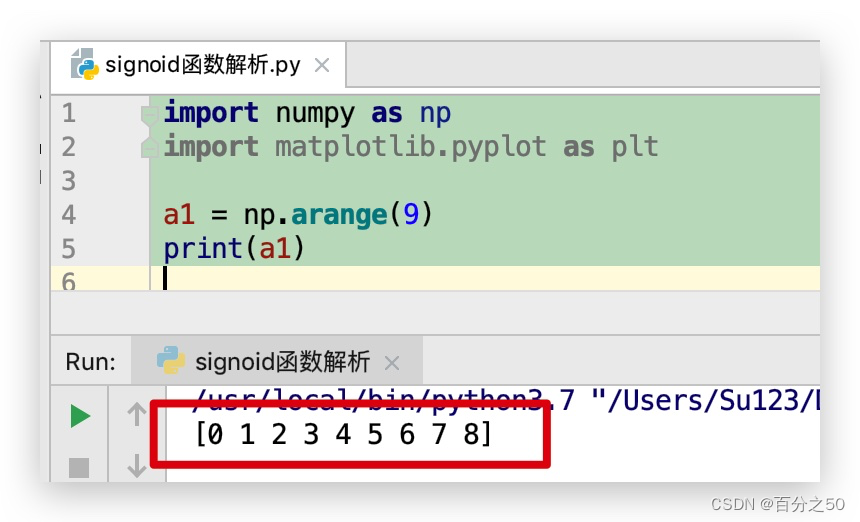
import numpy as np
import matplotlib.pyplot as plta1 = np.arange(9)
print(a1)3.2.2 绘制曲线
我们把这个数组画出来,使用matplotlib.pyplot的plot函数和show函数实现 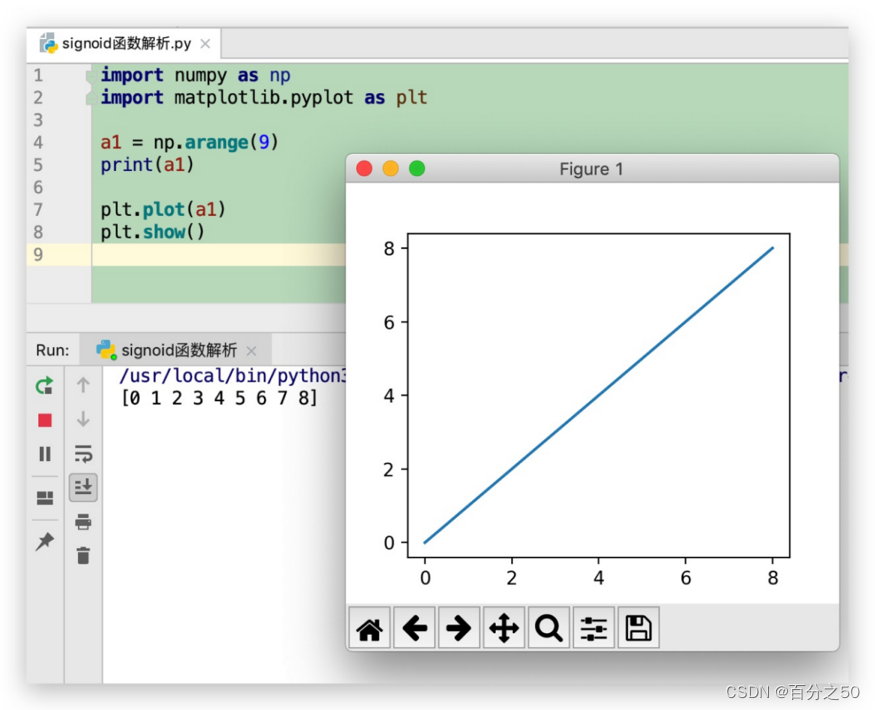 plot函数用于绘制曲线,当只传入一组数组时,x轴默认为0,1,2……,y轴为传入的值。
plot函数用于绘制曲线,当只传入一组数组时,x轴默认为0,1,2……,y轴为传入的值。
import numpy as np
import matplotlib.pyplot as plta1 = np.arange(9)
print(a1)plt.plot(a1)
plt.show()这样不够直观,我们在plot中增加一个参数 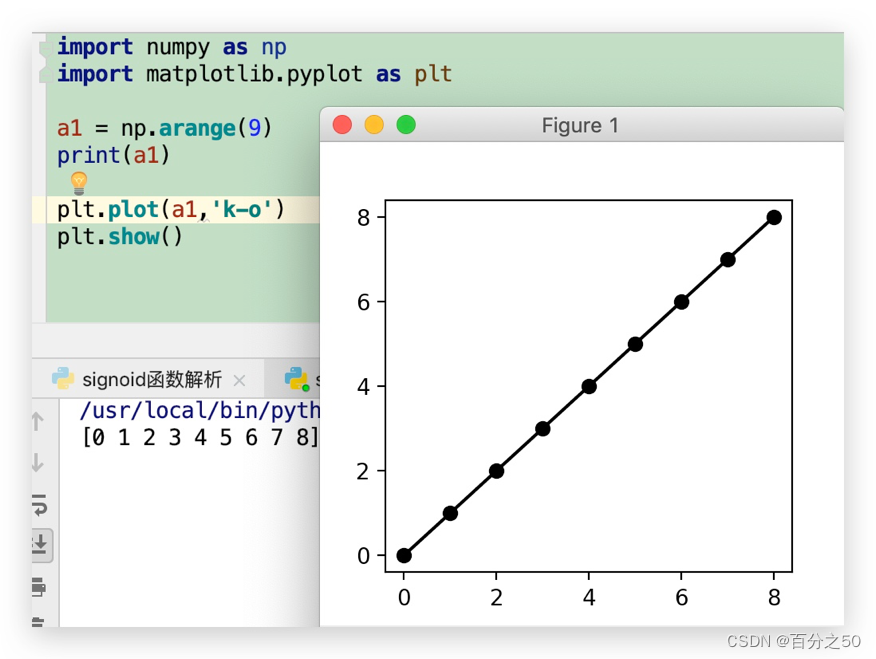
plt.plot(a1,’k-o’)中的k-o是设置所绘制图形的颜色、线条类型、图形类型,其中k表示黑色,-表示实线,o表示圆点, 这样子9个点都显示出来了。其他线条类型请参考 https://blog.csdn.net/qiurisiyu2016/article/details/80187177
3.3 Sigmoid公式
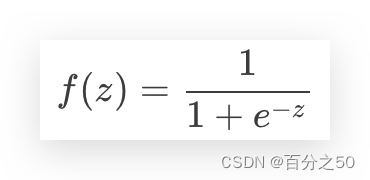
上面的公式的作用是将任意实数转换为0~1之间的数,方便后续处理,让我们看看它是如何实现的。
3.3.1 fz=-z
我们来一步一步解析,为了使数组更有代表性,我们给arange()函数传入两个参数 ,代表取数的范围从[-5,6),然后在plot()函数中加一个参数,让横坐标使用我们指定的数组:
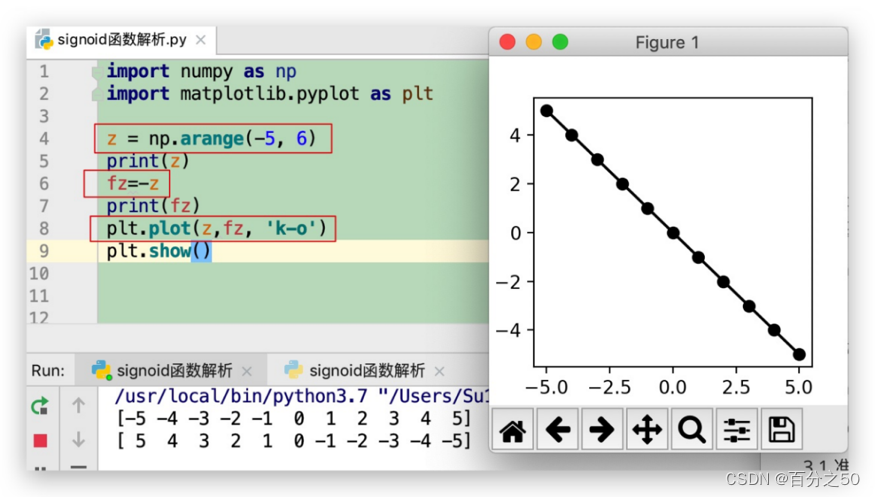
可以看到,绘制的曲线为一条斜率为-1的直线。
3.3.2 fz=np.exp(-z)
np.exp(z)是以e为底,以输入参数z为指数的指数函数,数学表达式为fz=e^z
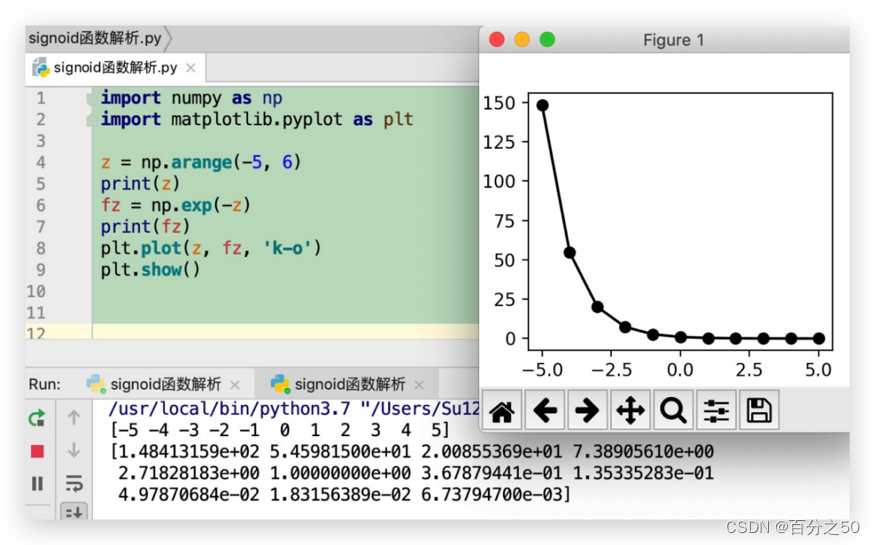
可以看到,绘制的曲线为一条递减的曲线,区间为(0,+∞),其中可以看到经典值e^0=1,e^1=2.718……(自然常数),由于小数点后位数较多,自动转换成了科学计数法,e表示10^,第一个数1.4841e+02即1.4841*10^2≈148,可以看到图中的 第一个点就在150附近。
3.3.3 fz=1+np.exp(-z)
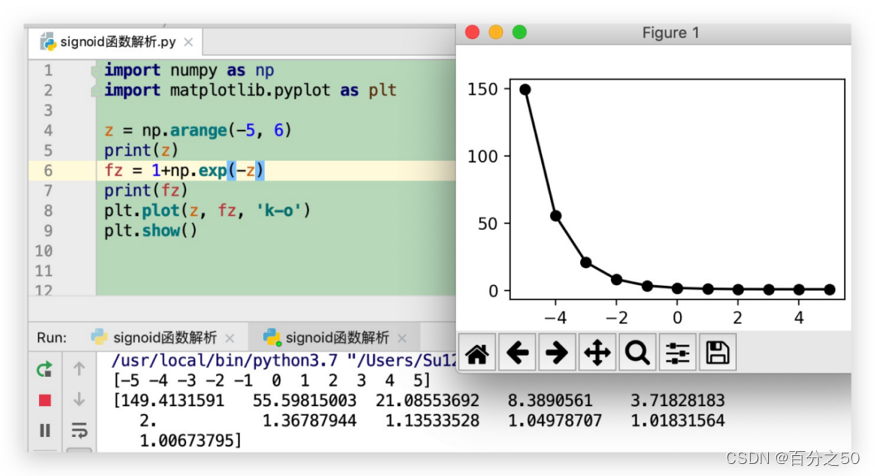
这一步非常重要,如果不进行这一步操作,后续在取倒数时,会发现值的区间超出1,比如当np.exp(-z)=0.1时,1/np.exp(-z)=10,这样整个函数的区间还是(0,+∞),对数据范围限制作用就没有了。
3.3.4 fz=1/(1+np.exp(-z))
这个就是神经网络中的激活函数Sigmoid公式的具体实现,我们看一下它的曲线
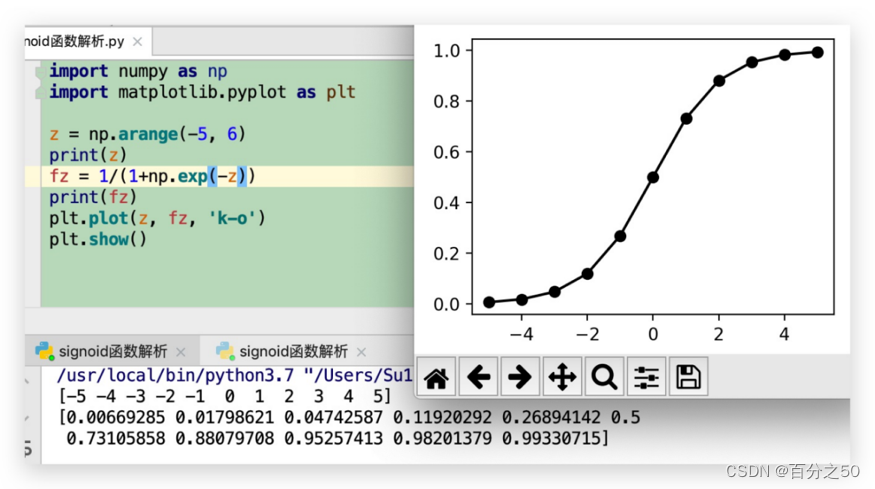
这个可以说是非常经典的曲线了,可以看到它是区间(0,1)的递增曲线,并且增长趋势是先加速后减速,类似在动画制作中的小车运动曲线。
但是在实际使用过程中,它依然会存在一些问题,比如在深度神经网络中梯度反向传递时导致梯度爆炸和梯度消失、收敛缓慢、幂运算求解耗时等等,具体缺点说明可以参考
https://blog.csdn.net/tyhj_sf/article/details/79932893
中的详细介绍。
3.4 tanh函数
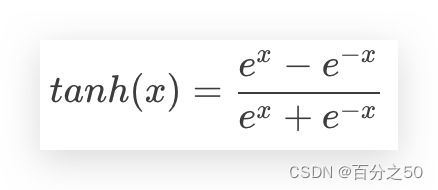
这个函数的取值区间为(-1,1) ,它的输出是0均值(原点左边+原点右边=0) ,一定程度上可以解决收敛缓慢的问题。
tanh(z)=(np.exp(z)-np.exp(-z))/(np.exp(z)+np.exp(-z))我们还是来慢慢解析它。
3.4.1 fz=np.exp(z)-np.exp(-z)
这个结构看起来复杂,我们拆成两部分
np.exp(z)
即e^z次方,看看指数爆炸一般的增长
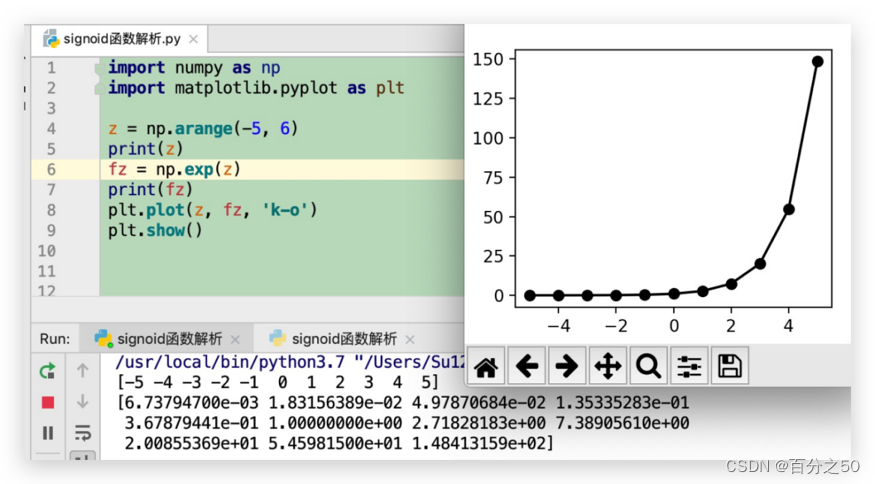
然后是np.exp(-z),这个图像我们之前有显示过了,就是曲线图形跟上面对称,递减的函数
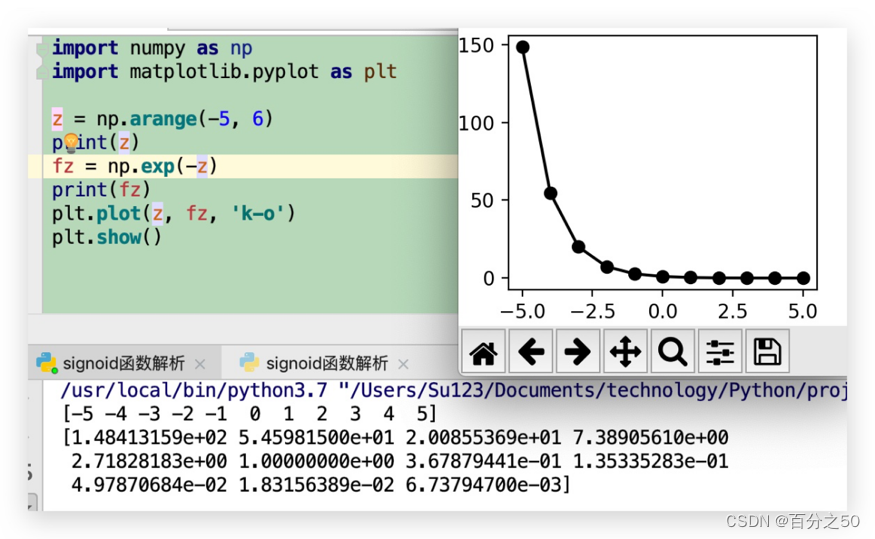
那么两个函数相减的图像是什么呢?
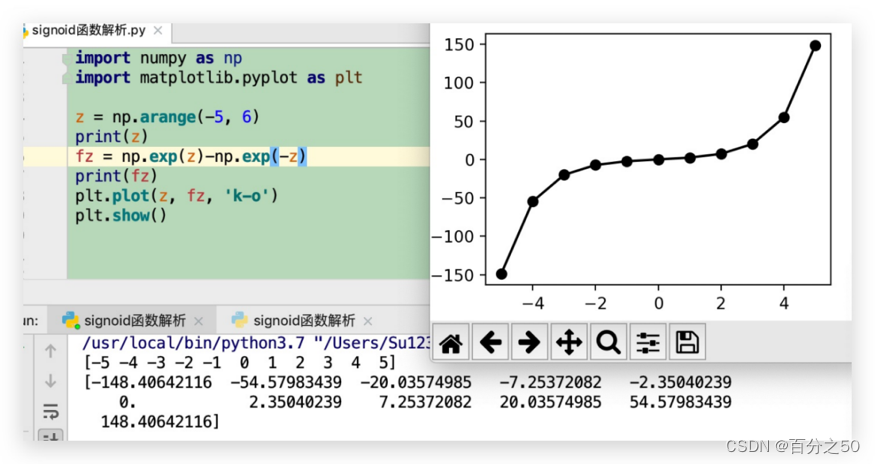
可以看到,这个图像跟sigmoid图像的曲线趋势可以说完全相反,它先加速上升,然后中间缓慢,后面又加速上升,有点像我们学习新东西的过程,一开始大量吸收知识点快速上升,到了瓶颈期进展缓慢,过了以后又快速发展。
3.4.2 fz=np.exp(z)+np.exp(-z)
两个函数相加,可以猜到的是,他们会形成一个抛物线(开口朝下)
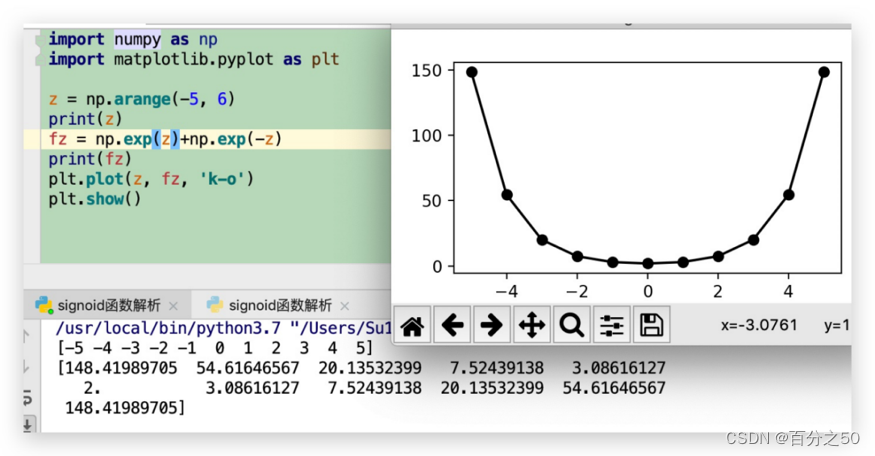
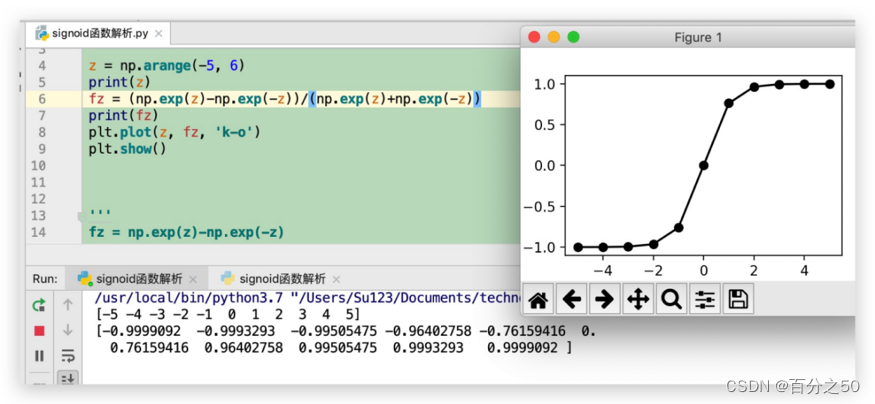
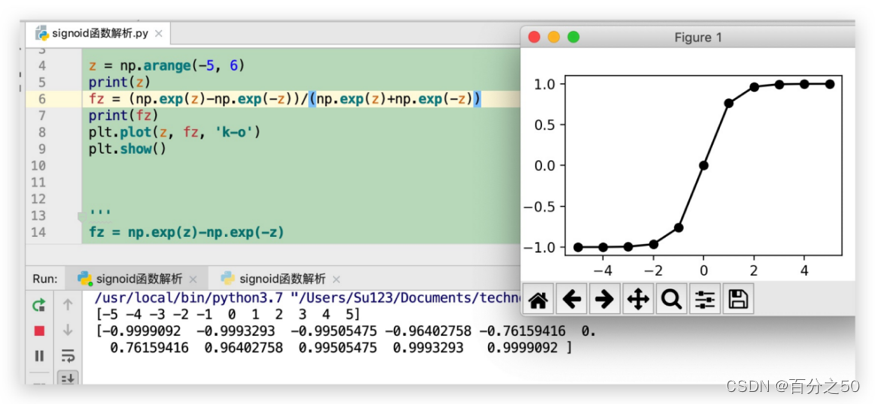
3.4.3 fz=(np.exp(z)-np.exp(-z))/(np.exp(z)+np.exp(-z))
tanh函数之前介绍过,它是一个区间(-1,1)的函数,由一个递增函数与一个抛物线函数之商所得,它的特点如前所述,取值区间为(-1,1) ,输出是0均值(原点左边+原点右边=0)。
3.5 Relu函数
目前比较流行的一种函数,ReLU虽然简单,但却是近几年的重要成果,有以下几大优点: 1) 解决了gradient vanishing问题 (在正区间) 2)计算速度非常快,只需要判断输入是否大于0 3)收敛速度远快于sigmoid和tanh
公式如下:
Relu=max(0,x)
它是分区间的函数,当z取值大于0时,取z值本身,小于等于0时,取0,函数实现及图像如下:
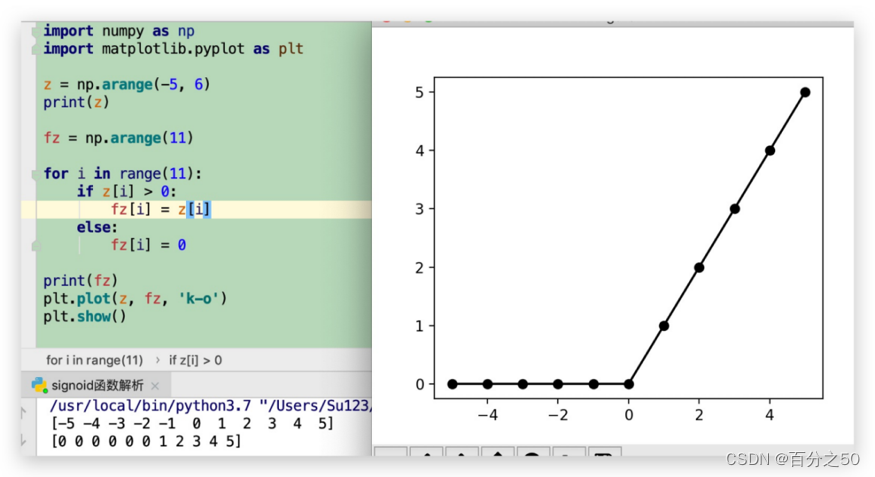
import numpy as np
import matplotlib.pyplot as pltz = np.arange(-5, 6)print(z)
fz = np.arange(11)
for i in range(11):if z[i] > 0:fz[i] = z[i]else:fz[i] = 0print(fz)plt.plot(z, fz, 'k-o')plt.show()