---

题目描述

给定二叉树的根节点 root ，返回所有左叶子之和。

示例 1：

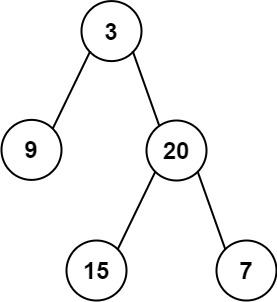
输入: root = [3,9,20,null,null,15,7]
输出: 24
解释: 在这个二叉树中，有两个左叶子，分别是 9 和 15，所以返回 24
示例 2:

输入: root = [1]
输出: 0

提示:

节点数在 [1, 1000] 范围内
-1000 <= Node.val <= 1000

解题思路

这个问题使用后序遍历和层序遍历都是可以的，只需要在遍历的过程中判断一下当前节点的左孩子节点是否是左叶子节点。如果是的话就加起来。
下面附上后序遍历的递归解法

代码

class Solution {public int sumOfLeftLeaves(TreeNode root) {//使用前序遍历的递归方法，每次递归到一个节点的时候就判断是否是左孩子//递归出口if (root == null) {return 0;}int leftNum = 0;//表示左子树中左叶子节点之和int rightNum = 0;//表示右子树中左叶子节点之和//如果左子树不为空，就判断一下这个节点是否会是左叶子if (root.left!=null){//如果是左叶子就给leftNum加上这个左叶子的valif (root.left.left == null && root.left.right == null) {leftNum = sumOfLeftLeaves(root.left) + root.left.val;} else {leftNum = sumOfLeftLeaves(root.left);}}else {//左子树为空的话也不需要单独处理，直接往下递归就行，如果为空的话自然下一步就返回0了leftNum = sumOfLeftLeaves(root.left);}//往右子树那一侧递归统计rightNum = sumOfLeftLeaves(root.right);//返回左右子树中左叶子节点的总和return leftNum + rightNum;}
}