本文来源公众号“python”,仅用于学术分享,侵权删,干货满满。
原文链接:Python 中检查一个数字是否是三态数
在数学中,三态数(Triangular Number)是一种特殊的数列,它是由自然数按照一定规律排列而成的。具体来说,第n个三态数可以用一个等差数列的和来表示,通常表示为T(n),公式为:
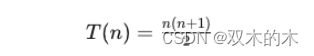
例如,前几个三态数分别是1, 3, 6, 10, 15, 21, ...。
本文将详细介绍如何在Python中检查一个数字是否是三态数,包括数学原理、算法实现和示例代码。
1 三态数的数学原理
三态数是一种等差数列的和,其数学原理比较简单。通过观察三态数的序列,可以发现每个三态数都是前一个三态数加上当前的自然数。具体来说,第n个三态数可以通过以下公式计算得到:
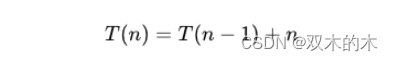
其中,T(0) = 0 是第一个三态数。
2 检查一个数字是否是三态数的算法实现
基于上述数学原理,可以编写一个函数来检查一个数字是否是三态数。
该函数的实现思路如下:
-
初始化一个变量
total为0,用于存储当前的三态数。 -
从1开始迭代自然数,对于每个自然数n,更新
total为total + n。 -
如果
total等于输入的数字,则该数字是三态数;否则,不是三态数。
下面是一个简单的Python函数来实现这个算法:
def is_triangular_number(num):total = 0n = 1while total < num:total += nif total == num:return Truen += 1return False
3 示例代码
通过一些示例代码来演示如何使用上述函数来检查一个数字是否是三态数。
# 检查一个数字是否是三态数
def is_triangular_number(num):total = 0n = 1while total < num:total += nif total == num:return Truen += 1return False# 测试示例
test_numbers = [1, 3, 6, 10, 15, 21, 22, 25]for num in test_numbers:if is_triangular_number(num):print(f"{num} 是三态数")else:print(f"{num} 不是三态数")
运行上述示例代码,将会输出以下结果:
1 是三态数
3 是三态数
6 是三态数
10 是三态数
15 是三态数
21 是三态数
22 不是三态数
25 不是三态数
4 实际应用场景
虽然三态数在数学中没有太多实际应用场景,但是其概念和相关算法思想可以应用到一些计算问题中。
4.1 搜索算法
在搜索算法中,有时候需要在一个有序的数据集合中进行搜索,判断某个元素是否存在。如果数据集合是一个三态数序列,可以利用三态数的性质来实现一种高效的搜索算法。
def search_triangular_number(target):total = 0n = 1while total < target:total += nif total == target:return Truen += 1return False# 示例:在三态数序列中搜索目标数字
target_numbers = [6, 10, 15, 21]for num in target_numbers:if search_triangular_number(num):print(f"{num} 存在于三态数序列中")else:print(f"{num} 不在三态数序列中")
在上面的示例中,定义了一个函数search_triangular_number来搜索一个目标数字是否存在于三态数序列中。如果目标数字是一个三态数,就返回True;否则返回False。这种搜索算法的时间复杂度是O(sqrt(n)),相比于线性搜索更加高效。
4.2 数据结构设计
在一些数据结构设计中,三态数的概念可以被用来设计一些有序的数据结构。例如,可以利用三态数的性质来设计一种高效的索引结构,用于快速查找和访问数据。
class TriangularIndex:def __init__(self, size):self.index = [n * (n + 1) // 2 for n in range(size)]def contains(self, target):return target in self.index# 示例:使用三态数索引结构
index = TriangularIndex(10)target_numbers = [6, 10, 15, 21]for num in target_numbers:if index.contains(num):print(f"{num} 存在于三态数索引结构中")else:print(f"{num} 不在三态数索引结构中")
在上面的示例中,定义了一个TriangularIndex类来实现一个简单的三态数索引结构。该索引结构可以用来快速判断一个数字是否存在于三态数序列中,从而提高数据访问的效率。
4.3 编程练习
检查一个数字是否是三态数也可以作为一种编程练习,帮助提高编程能力和算法思维。通过编写代码实现这个功能,可以加深对数学概念和算法思想的理解,提高代码的编写和调试能力。
def is_triangular_number(num):total = 0n = 1while total < num:total += nif total == num:return Truen += 1return False# 编程练习:检查一系列数字是否是三态数
numbers_to_check = [28, 36, 45, 55]for num in numbers_to_check:if is_triangular_number(num):print(f"{num} 是三态数")else:print(f"{num} 不是三态数")
通过编程练习,可以加深对三态数的理解,并且熟练掌握相关的算法实现。
5 总结
本文介绍了三态数的数学原理、检查一个数字是否是三态数的算法实现以及示例代码。通过了解三态数的概念和算法思想,可以更好地理解数学中的等差数列,并将其应用到实际的编程问题中。希望本文能够帮助大家更加深入地理解三态数,并能够灵活运用相关的算法思想。
如果你觉得文章还不错,请大家收藏、 点赞、分享、评论 下,因为这将是我持续输出更多优质文章的最强动力!
THE END!
文章结束,感谢阅读。您的点赞,收藏,评论是我继续更新的动力。大家有推荐的公众号可以评论区留言,共同学习,一起进步。